CF336A Vasily the Bear and Triangle 题解

Content

一个矩形的顶点为 \((0,0)\)，其对顶点为 \((x,y)\)，现过 \((x,y)\) 作直线，分别交 \(x\) 轴和 \(y\) 轴于 \(A,B\) 两点，使得 \(\triangle OAB\) 为一个等腰直角三角形，求 \(A,B\) 点的坐标。（输出时 \(x\) 坐标小的先输出）

数据范围：\(-10^9\leqslant x,y\leqslant 10^9,x,y\neq 0\)。

Solution

这题是个数学题目，需要用到分类讨论。

这里先把草图给放上，方便大家理解——

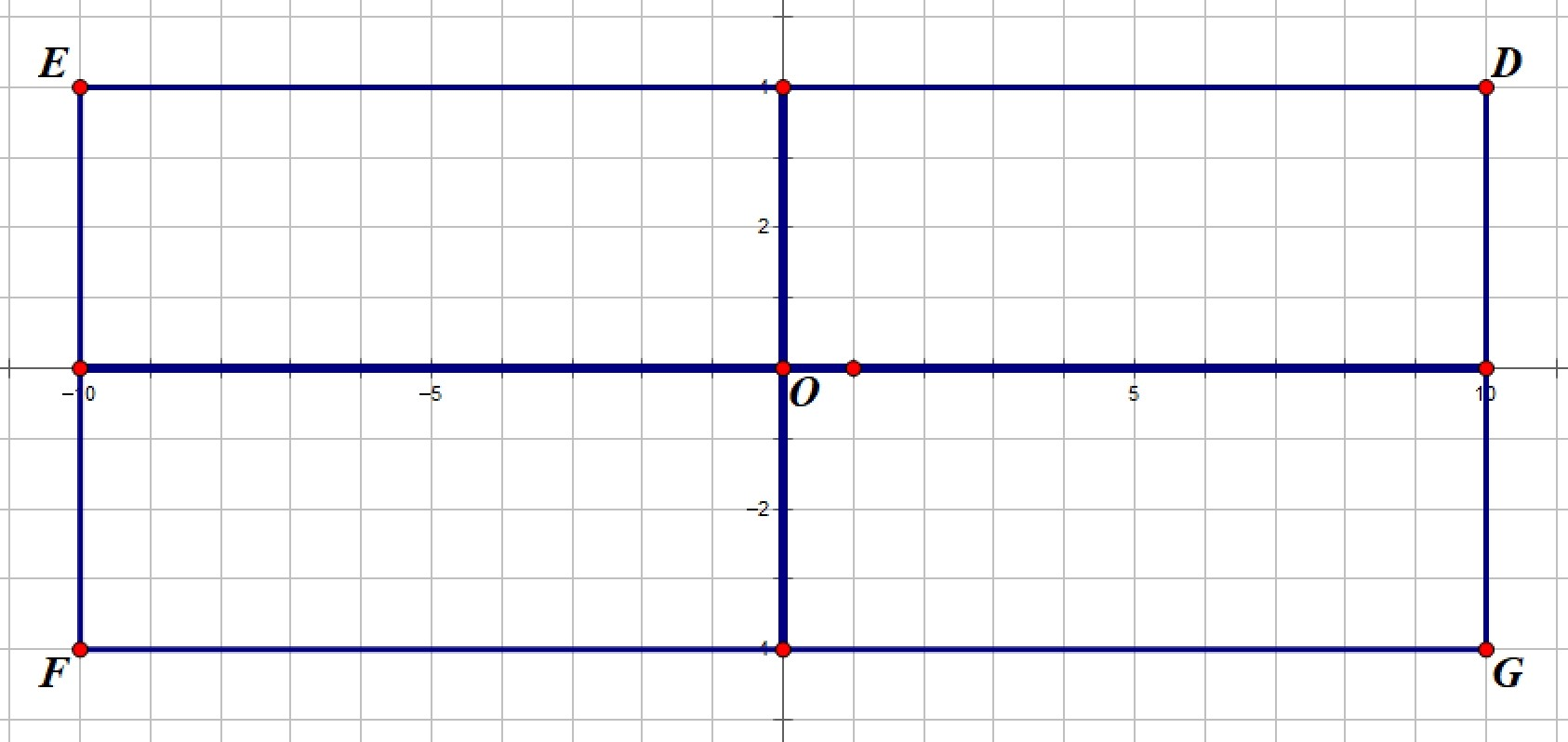
当 \(x>0,y>0\)，即 \((x,y)\) 在第一象限时，即如上图中 \(D\) 点所示。那么设我们过 \(D\) 点做的直线分别交 \(x,y\) 轴于 \(A_1,B_1\) 两点，并过 \(D\) 点做 \(DH_1\perp OA_1\)。则有 \(\angle DA_1O=45^\circ\)。所以 \(\triangle DH_1A_1\) 是一个等腰直角三角形，所以 \(H_1A_1=DH_1=|x|=x\)。同理，过 \(D\) 点做 \(DH_2\perp OB_1\)，则有 \(\angle DB_1O=45^\circ\)，所以 \(\triangle DH_2B_1\) 是一个等腰直角三角形，所以 \(B_1H_2=DH_2=|y|=y\)。所以 \(A_1\) 的横坐标为 \(OH_1+DH_1=x+y\)，\(B_1\) 的纵坐标为 \(OH_2+B_1H_2=x+y\)。所以最终的结果就是 \(A_1(x+y,0),B_1(0,x+y)\)。

这里以第一象限的为例，其他的就请读者自己去推啦~

Code

#include <cstdio>
using namespace std;

int main() {
	int a, b;
	scanf("%d%d", &a, &b);
	if(a > 0 && b > 0)		printf("0 %d %d 0", a + b, a + b);
	else if(a < 0 && b > 0)	printf("%d 0 0 %d", a - b, -a + b);
	else if(a < 0 && b < 0)	printf("%d 0 0 %d", a + b, a + b);
	else if(a > 0 && b < 0)	printf("0 %d %d 0", a - b, -a + b);
	return 0;
}