Coursera Deep Learning笔记 结构化机器学习项目 （上）

参考：https://blog.csdn.net/red_stone1/article/details/78519599

1. 正交化(Orthogonalization)

机器学习中有许多参数、超参数需要调试。

通过每次只调试一个参数，保持其它参数不变而得到的模型某一性能改变是一种最常用的调参策略，我们称之为正交化方法（Orthogonalization）。

对应到机器学习监督式学习模型中，可以大致分成四个独立的“功能”：

• Fit training set well on cost function

  • 优化训练集可以通过使用更复杂NN，使用Adam等优化算法来实现

• Fit dev set well on cost function

  • 优化验证集可以通过正则化，采用更多训练样本来实现

• Fit test set well on cost function

  • 优化测试集可以通过使用更多的验证集样本来实现

• Performs well in real world

  • 提升实际应用模型可以通过更换验证集，使用新的cost function来实现

这些调节方法只会对应一个“功能”，是正交的。

2. 单一数字评估指标(Single number evaluation metric)

构建、优化机器学习模型时，单值评价指标非常必要。有了量化的单值评价指标后，我们就能根据这一指标比较不同超参数对应的模型的优劣，从而选择最优的那个模型。

• 精确率( precision)：反映了模型 判定的正例 中 真正正例 的比重。

  • 在垃圾短信分类器中，是指 预测出 的垃圾短信中真正垃圾短信的比例。

  • \(precison = \frac{TP}{TP+FP}\)

• 召回率{ recall)：反映了 总正例 中被模型 正确判定正例 的比重。

  • 医学领域也叫做灵敏度( sensitivity)。在垃圾短信分类器中,指所有真的垃圾短信被分类器正确找出来的比例。

  • \(recall = \frac{TP}{P}\)

• F值 ☆☆☆

  • F 值 (\(F_\beta-score\)) 是 精确率 和 召回率 的 调和平均：

    • \(F_\beta-score=\frac{(1+\beta^2)*precison*recall}{(\beta^2*precision+recall)}\)

    • \(\beta一般大于0。当\beta=1时，退化为 F1\)，即 \(F_1=\frac{2\cdot P\cdot R}{P+R}\)

    • \(F_1\) 是最常用的 评价指标，即 表示二者同等重要

• 例，有A和B两个模型，它们的准确率（Precision）和召回率（Recall）分别如下：

Classifier	Precision	Recall
A	95%	90%
B	98%	85%

然后得到了A和B模型各自的F1 Score：

Classifier	Precision	Recall	F1 Score
A	95%	90%	92.4%
B	98%	85%	91.0%

从F1 Score来看，A模型比B模型更好一些。通过引入单值评价指标F1 Score，很方便对不同模型进行比较。

3. 满足和优化指标(Satisficing and Optimizing metic)

有时候，要把所有的性能指标都综合在一起，构成单值评价指标是比较困难的。

• 解决办法是，我们可以把某些性能作为优化指标（Optimizing metic），寻求最优化值

• 而某些性能作为满意指标（Satisficing metic），只要满足阈值就行了

例，有A，B，C三个模型，各个模型的Accuracy和Running time如下：

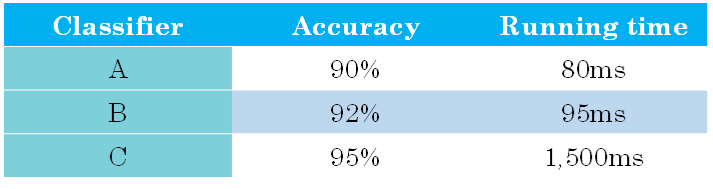
我们可以将Accuracy作为优化指标（Optimizing metic），将Running time作为满意指标（Satisficing metic）

给Running time设定一个阈值，在其满足阈值的情况下，选择Accuracy最大的模型。如果设定Running time必须在100ms以内，显然，模型C不满足阈值条件，首先剔除；模型B相比较模型A而言，Accuracy更高。

4. Train/dev/test distributions

应该尽量保证dev sets和test sets来源于同一分布且都反映了实际样本的情况。

如果dev sets和test sets不来自同一分布，那么我们从dev sets上选择的“最佳”模型往往不能够在test sets上表现得很好。

5. Size of the dev and test sets

• 当样本数量不多（小于一万）的时候，通常将Train/dev/test sets的比例设为60%/20%/20%，在没有dev sets的情况下，Train/test sets的比例设为70%/30%。

• 当样本数量很大（百万级别）的时候，通常将相应的比例设为98%/1%/1%或99%/1%。

• 对于dev sets数量的设置，遵循的准则是通过dev sets能够评价不同模型，以便选择出更好的模型。

• 对于test sets数量的设置，遵循的准则是通过test sets能够反映出模型在实际中的表现。

6. When to change dev/test sets and metrics

算法模型的评价标准：有时候需要根据实际情况进行动态调整，目的是让算法模型在实际应用中有更好的效果。

• 如，识别猫类的例子。初始的评价标准是错误率，算法A错误率为3%，算法B错误率为5%。

• 显然，A更好一些。但是，实际使用时发现算法A会通过一些色情图片，但是B没有出现这种情况。B可能对用户更好一点。

• 这时候，我们就需要改变之前单纯只是使用错误率作为评价标准，而考虑新的情况进行改变。例如增加色情图片的权重。

原来的cost function：

\[J=\frac1m\sum_{i=1}^mL(\hat y^{(i)},y^{(i)})
\]

更改评价标准后的cost function：

\[J=\frac{1}{w^{(i)}}\sum_{i=1}^mw^{(i)}L(\hat y^{(i)},y^{(i)}) \\
w^{(i)}=\begin{cases}
1, & x^{(i)}\ is\ non-porn\\
10, & x^{(i)}\ is\ porn
\end{cases}
\]

机器学习可分为两个过程：

• Define a metric（度量标准） to evaluate classifiers

• How to do well on this metric

总结：

7. Why human-level performance

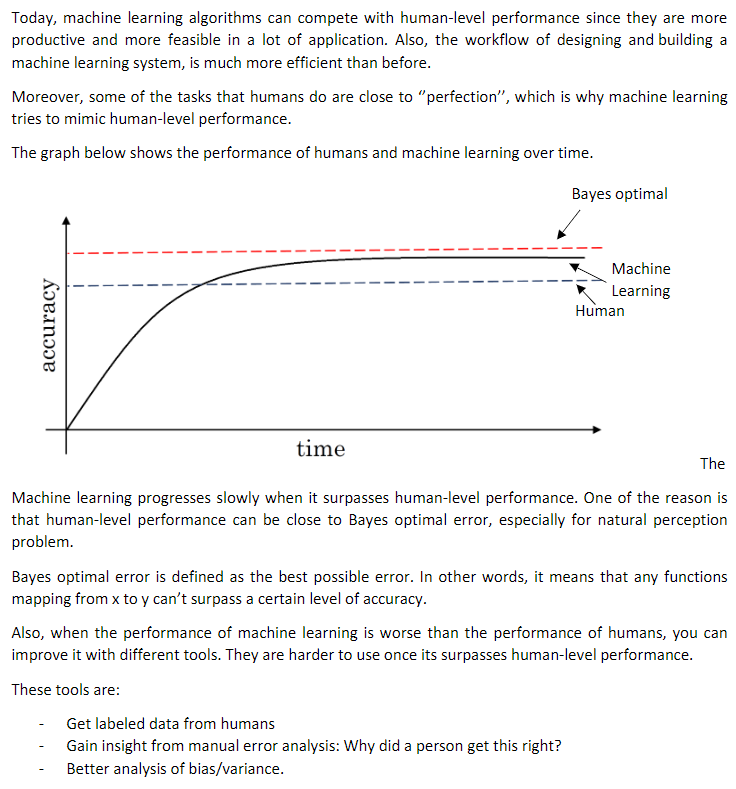
8. 可避免误差(Avoidable bias)

• 贝叶斯误差（对贝叶斯误差的估计） 和 Training Error 之间的差值 -- 可避免误差：误差有个无法超越的最低水平

• Training error 和 Dev error之间的差值，大概说明你的算法在方差问题上还有多少改善空间

如图，右边可避免误差在0.5%，2%是方差的指标（应该专注它）; 左边7%为可避免偏差大小（应该专注于它），2%方差大小；

9. Understanding human-level performance

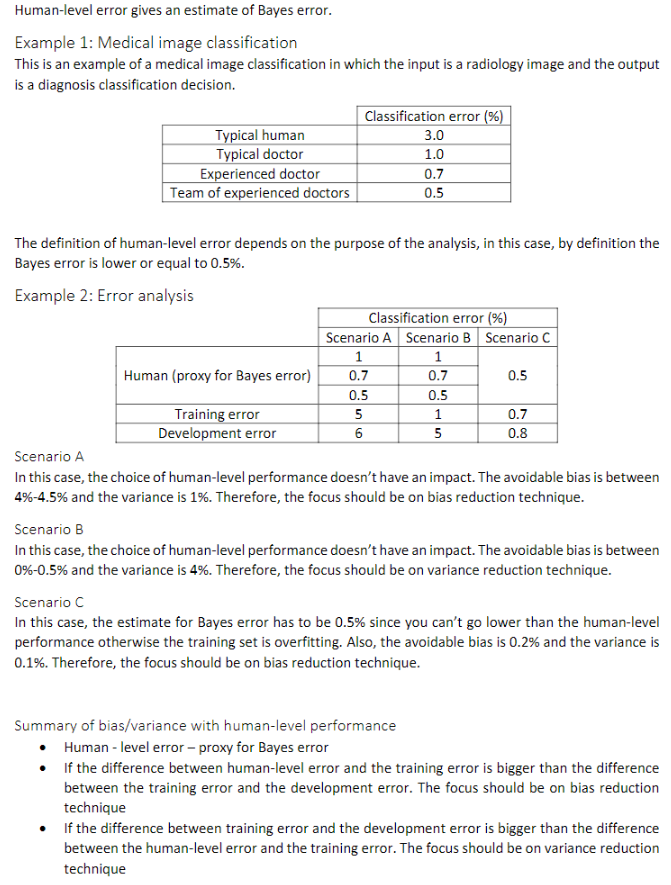
9. Understanding human-level performance

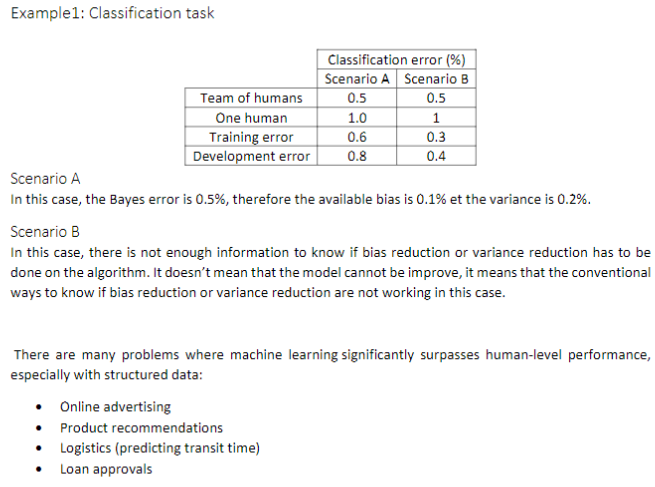
10. 改善模型表现