work2_求交点数

教学班级：周三上午三四节

项目地址：https://github.com/875571216/-

PSP表格

psp2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60	30
Estimate	估计这个任务需要多少时间	10	10
Development	开发
Analysis	需求分析 (包括学习新技术)	180	240
Design Spec	生成设计文档	30	10
Design Review	设计复审	10	10
Coding Standard	代码规范 (为目前的开发制定合适的规范)	10	10
Design	具体设计	50	50
Coding	具体编码	180	120
Code Review	代码复审	10	10
Test	测试（自我测试，修改代码，提交修改）	180	220
Reporting	报告	10	10
test Reporting	测试报告	30	20
Size Measurement	计算工作量	10	10
Postmortem & Process Improvement Plan	事后总结, 并提出过程改进计划	10	10

解题思路描述

1）首先把输入文件中的直线，圆的信息都构造成相应的对象，存入到各自的容器中。（直线、圆和点各设置一个动态数组容器vector来存储）

2）交点分为：直线与直线相交；直线与圆相交；圆与圆相交，在各自的类中设置求交点的成员方法。具体求法为：

<1> 直线l1与直线l2：联立解方程

<2> 直线l与圆c：求出一条经过圆c的圆心且与直线l垂直的直线_l，l与_l的交点是c的圆心作l的垂线的垂足，通过这个垂足可以求出两个交点。

<3> 圆c1与圆c2：两圆的方程相减到它们焦点所在的直线，然后求直线与圆的交点。

3）交点加入加点集合（查重的方法是暴力遍历，如果这个点在数组中已经存在，就不加入集合，没找到更好的方法）

设计实现过程。

1）代码如何组织：

<1> 头文件：定义了line（直线）、dot（点）、cycle（圆）三个数据类型。

<2> 主体cpp文件：引用了头文件的三个数据类型。定义了line（直线）类中的“两直线求交点”的方法。定义了cycle（圆）类中“两圆求交点”的方法以及“圆与直线求交点”的方法。最后还有从文件读入圆与直线信息并构造相应数据类型的的main函数。

<3> 单元测试：设置了10组单元测试，引用了头文件中的三个数据类型，这三个数据类型的具体成员方法在主体cpp文件中定义好了。

2）单元测试：

<1> 直线与直线相交；

<2> 直线与直线平行；

<3> 圆与圆相离；

<4> 圆与圆外切；

<5> 圆与圆相交；

<6> 圆与圆内切；

<7> 圆包含圆；

<8> 直线与圆相离；

<9> 直线与圆相切；

<10> 直线与圆相交；

性能分析

可以看到，我的程序中，占用cpu最多的是solve，这个函数是我用来封装计算所有交点的函数，占用率高很正常。然后就是lintersectl这个函数，这个是用来计算直线交点的，由于我的测试样例只计算了直线与直线相交，这也比正常。有问题的是dotinsert这个函数，这个函数是用来插入点的，为什么会占用这么多的cpu呢，因为我的设计，是通过比较点的坐标来判断该点是否已经加入了交点集。我存储交点的数据结构是一个数组，这就导致没插入一个点就必须遍历一边数组，占用大量的cpu资源。看图：



我的改进办法是用hash表来存储交点，这样每次插入点的复杂度就有o(n)变成了o(1)，节省了大量的时间开销。

关键代码：

<1> 两直线求交点方法：简单解方程。



<2> 直线l与圆c求交点的方法：求出一条经过圆c的圆心且与直线l垂直的直线_l，l与_l的交点是c的圆心作l的垂线的垂足。然后通过点到直线距离公式求圆c的圆心到直线l的垂直距离d。用勾股定理就能算出垂足点到两交点的距离，再结合直线l斜率，就可以求出两交点坐标。当然，如果圆心到直线的垂直距离d大于圆半径，那就没有交点，相等则只有一个交点——垂足点。



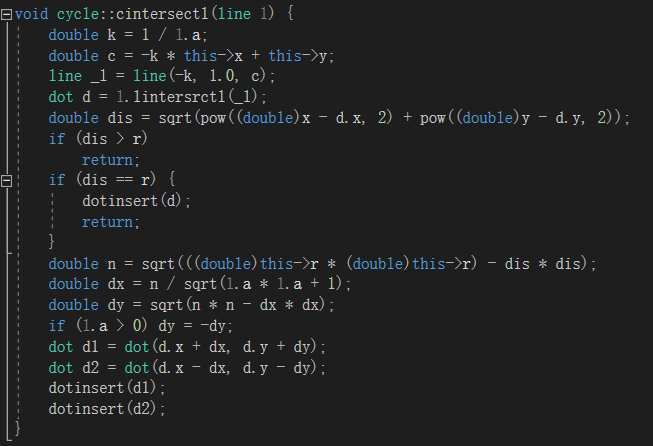
<3> 两圆相交：首先求出两圆心之间的距离d，如果d>r1+r2(两圆半径之和)或者d+r1(较小圆的半径)<r2，那么两个圆没有交点。然后从两个圆方程中解出通过他们交点的直线，再求直线与圆的交点



可以看出，确实大部分时间都消耗在了遍历数组上。于是，我决定用hash表来存储交点集，这样，在查找点集时的复杂度就有o(n)变为o(1)，节省了大量的时间开销。