【1】Embarrassingly Parallel（易并行计算问题）

1、什么是Embarrassingly Parallel（易并行计算问题）

易并行计算问题：A computation that can be divided into a number of  completely independent tasks。在编写并行程序过程中，首先需要将一个问题分解成若干部分，然后将每个部分分配给不同的processer（处理器）或者thread（线程）分别进行计算，如果该计算问题能够被分解成一些完全独立的子计算（task）、同时各个task之间数据几乎没有依赖，没有通信。那这个计算问题就叫作易并行计算问题。

对于该问题一般程序处理流程如下：

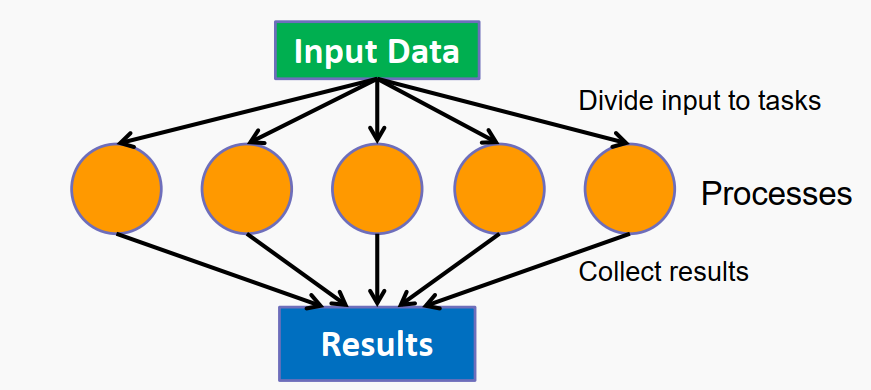
对于输入的Data，直接拆分成几块互相没有依赖的Subdata,每一份Subdata具有完全相同的处理方式，最后再将subdata的处理结果合并行输出，对于这类数据计算问题，就天然的适用于并行计算。尤其是在图像处理方面，并行处理的情况很多。

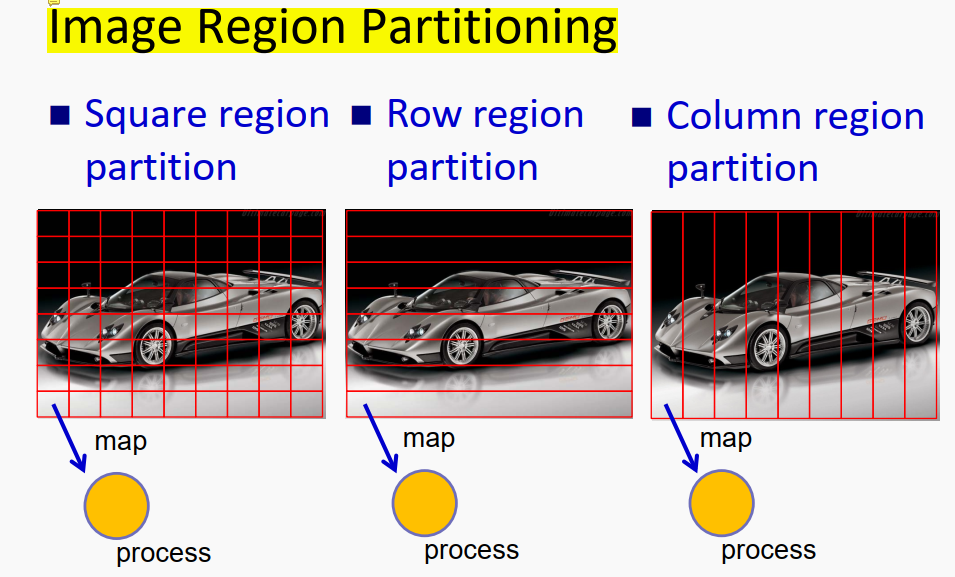
在对图像进行平移、旋转、缩放过程中，对于每一个pixel(像素点)数据都是完全相同的操作，当然我们可以写一个两层for循环，遍历每个pixel，然后对每个pixel进行转换，但这样效率很低。按照并行编程的思路，我们可以对一幅图像不同的像素点进行拆分，送到不同processer，同时进行图像计算，这样就实现了图像计算的加速。理想情况下，对于每个piexl，咱们都送到一个processer中进行计算，这样效率最高。但实际情况是，往往processer或者thread开启的数量也是有限度的，就像高速公路分流一样，不可能无限制的扩宽车道，所以咱们需要对一整个Data进行合理的拆分，将一块数据送入processer中进行处理。正如上图所示，对于原始图像的拆分可以分块、分行、分列，不同的分割方式对最后运行效率也是有一定影响的。

2、易并行计算需要考虑的问题

对于易并行计算问题，虽然数据很容易进行拆分处理，但在实际编写程序过程中往往会遇到两个问题，首先我们看一下并行编程的程序框架。

对于图像的平移处理，一般并行程序由主从结构构成，主程序用来对数据进行拆分，送到不同的process中，并接受不同process的返回值。

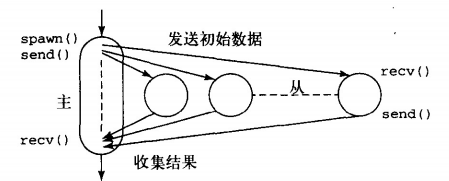
主程序

//master process 对于480*640的图像
for(i=0, row=0; i<48; i++, row+=10) // for each of 48 processes 按行拆分
{
	send(row, Pi); // send row no.
} //数据拆分 以及发送
for(i=0; i<480; i++){
  for(j=0; j<640; j++) {
    temp_map[i][j] = 0; // initialize temp 缓冲数组
  }
}
for(i=0; i<(480*640); i++) { // for each pixel
	recv(oldrow, oldcol, newrow, newcol, PANY); // accept new coordinates 数据接收
	if !((newrow<0)||((newrow>=480)||(newcol<0)||((newcol>=640)){
		temp_map[newrow][newcol] = map[oldrow][oldcol];
    }
}
for(i=0; i<480; i++){
  for(j=0; j<640; j++) {
    map[i][j] = temp_map[i][j]; // update map 更新图像
  }
}

子程序

// slave process
recv (row, Pmaster);
for (oldrow = row; oldrow < (row+10); oldrow++) // for each row in the partition 局部线性处理
{
	for (oldcol = 0; oldcol < 640; oldcol++) { // for each column in the row
		newrow = oldrow + delta_x; // shift along x-dimension
		newcol = oldcol + delta_y; // shift along y-dimension
		send(oldrow, oldcol, newrow, newcol, Pmaster); // send out new coordinates
	}
}

上述程序框架就是完全按照主从结构进行编写的，我们可以发现，在master process中我们需要完成数据拆分、发送、接收。在slave process中我们需要完成数据计算（对于embarrassingly parallel来说这部分相对简单）。

按照上述程序框架我们需要在master process中考虑：一、数据如何拆分；二、各个subdata如何合理的分配到不同的processer（ Load Balancing 负载均衡）；因为往往并行程序的执行时间是由执行时间最长的process决定的，所以尽量让每个processer平均高效的完成工作才是最重要的。

3、易并行程序的优化

   在给processer分配任务过程中，主要分为两大类： Static Load-Balancing （静态分配）、 Dynamic Load Balancing （动态分配）。  

3.1、Static Load-Balancing （静态分配）

    常见的静态分配有 1、Round robin algorithm — selects processes in turn   2、 Randomized algorithms — selects processes randomly 

静态分配就如上面这个程序处理逻辑一样，在master中就将subdata分割好，每个processer中传入的subdata是可以确定的，对于简单的问题这样分配任务是没问题的，但是对于复杂的问题（尤其是不同的subdata执行的时间不同），那这样静态分配会导致有些processer特别忙、有些processer又处于空闲，导致如下的时间分配问题：

就像单位用人一样，相同的任务量不同的人完成的时间不同，需要根据能力分配任务，能者多劳，照顾新人。

3.2、Dynamic Load Balancing （动态分配）

        一般来说对于复杂并行处理问题，尤其是无法确定slave process处理时间的问题，都需要用到动态分配。常见的动态分配算法有：1、 Centralized Work Pool ；2、 Decentralized Work Pool ；3、Fully Distributed Work Pool 。

   3.2.1 Centralized Work Pool（工作池）

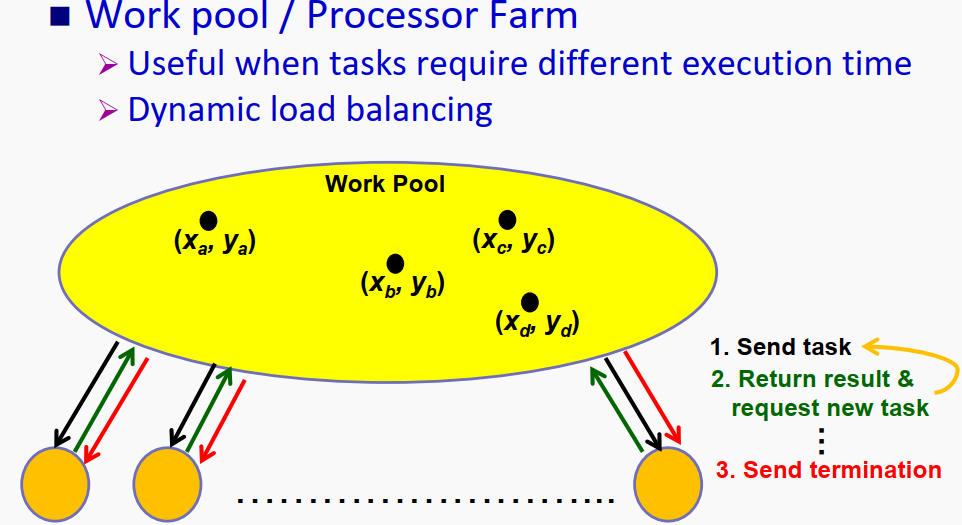
      先上程序框架：

主程序

//master process
count = 0; // # of active processes
row = 0; // row being sent
for (i=0; i<num_proc; i++) { // send initial row to each processes
	send(row, Pi , data_tag); //先轮流送给每一个processer
	count++;
	row++;
}
do {
	recv(&slave, &r, color, PANY , result_tag); //收到某个线程完成的工作结果
	count--;
	if (row < num_row) { // keep sending until no new task 如果row还没完成
		send(row, Pslave , data_tag); // send next row  发送下一行数据
		count++;
		row++;
	}
  	else {
		send(row, Pslave , terminate_tag); // terminate 让这个process终止
	}
	display(r, color); // display row
} while(count > 0);

从程序

//slave process P ( i )
recv(&row, Pmaster , source_tag);
while (source_tag == data_tag) { // keep receiving new task
	c.imag = min_imag + (row * scale_image);
	for (x=0; x<640; x++) {
		c.real = min_real + (x * scale_real);
		color[x] = cal_pixel (c); // compute color of a single row
	}
	send(i, row, color, Pmaster , result_tag); // send process id and results
	recv(&row, Pmaster , source_tag);
}

      上述程序其实是用来计算曼德勃罗数集的一部分，首先master连续的给所有processer分配任务，谁先做完任务则回来取下一个任务，这样就实现了基本的动态平衡。

 3.2.2  Decentralized Work Pool （分散的工作池）

 

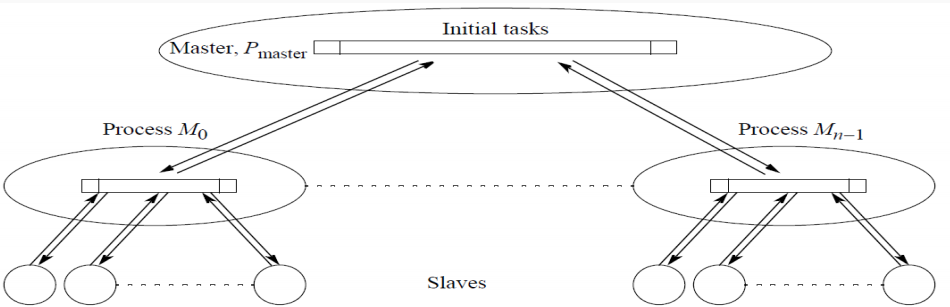
       这个动态分配算法，是在 Centralized Work Pool（工作池）上进行的改进，前者完全依赖master来分配任务，这里在每个processer中可以再进行一次任务的分配。

3.3.3  Fully Distributed Work Pool （完全分布式的工作池）

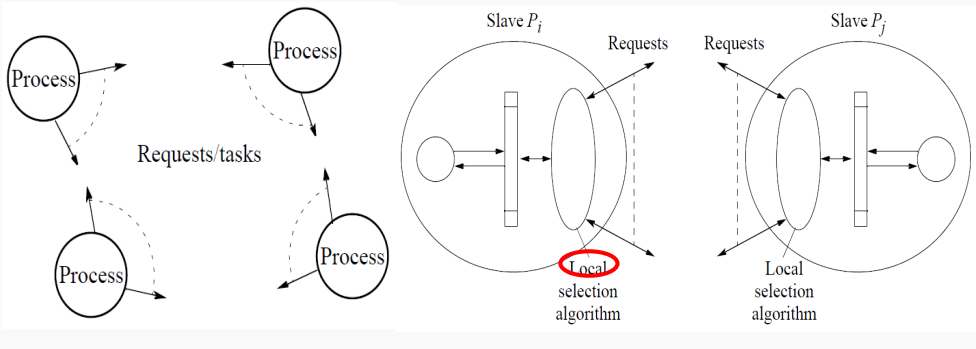
特点： 每个process拥有或生成自己的任务，而且process之间互相通信可以互相传递任务（偷任务），很明显这种结构程序逻辑编写难度较大、而且processer之间的通信压力也很大，但是任务分配的更加平均。

4、易并行程序举例

CS542200 Parallel Programming 中的 Homework 2:要求计算Mandelbrot Set（曼德勃罗数集），等啥时候写完啥时候上传吧。先贴一张Mandelbrot Set图。曼德勃罗数集一般用于图像分形学，而且每个像素点的迭代时间无法确定（属于易并行编程问题，但需要动态分配任务）。

-----------------------------------------------------------------------------

上述图片摘自《CS542200 Parallel Programming 》、《并行程序设计》

该文章为原创，转载请注明出处。

-----------------------------------------------------------------------------