【机器学习基础】逻辑回归—

LR算法作为一种比较经典的分类算法，在实际应用和面试中经常受到青睐，虽然在理论方面不是特别复杂，但LR所牵涉的知识点还是比较多的，同时与概率生成模型、神经网络都有着一定的联系，本节就针对这一算法及其所涉及的知识进行详细的回顾。

LogisticRegression

0.前言

　　LR是一种经典的成熟算法，在理论方面比较简单，很多资料也有详细的解释和推导，但回过头再看LR算法会有很多全新的认识，本节就从LR的引入到原理推导以及其与神经网络的有何联系串联起来，可以加深对这方面知识的理解。本节首先从概率生成模型引入LR，然后基于二分类推导LR的算法过程，再介绍LR在多分类中的应用，最后介绍LR与神经网络的联系，并通过一些实例对LR进行实现。

1.LR简介

　　LR回归是将样本进行线性叠加之后，再通过sigmoid函数，来对样本进行分类的过程，sigmoid函数如下：

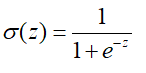
　　其图形如下：

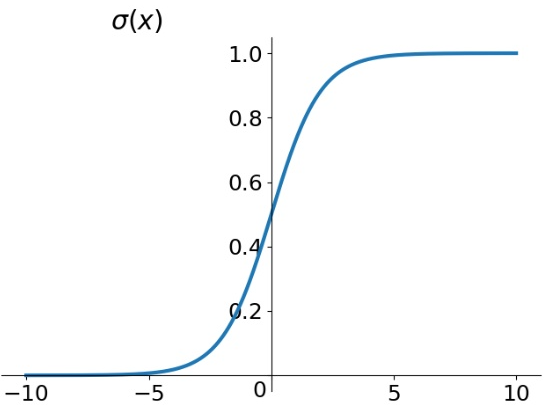
　　可以看到当z>0时，通过sigmoid函数后，σ(z)>0.5，z<0时，σ(z)<0.5;

　　那么LR的具体做法就是：

　　（1）找到一组参数w、b，求得样本的线性叠加z=wx+b；

　　（2）然后将z通过sigmoid函数，如果>0.5，则属于类别1，否则属于类别2；

　　然后其训练过程就是寻找参数w、b的过程，后面再说如何进行训练。

2.从概率模型到LogisticRegression

　　前面有一节有关概率模型专题，详见https://www.cnblogs.com/501731wyb/p/15149456.html，通过假设样本分布，利用最大似然估计来估计样本分布参数，从而求解给定一个样本属于C1和C2的概率，来进行分类的过程，记给定一个未知样本X，属于C1的概率为P(C1|X),那么，根据贝叶斯公式：

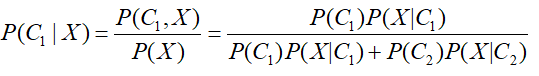
　　对上面的公式变形，上下同除以分子，得到：

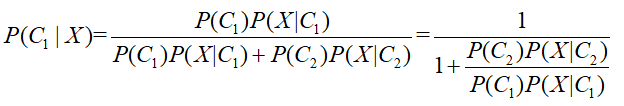
　　则有：

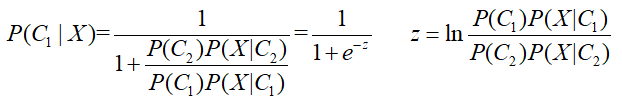
　　这里注意z的“分子”和“分母”与原式中正好相反，因为有“-”号。

　　通过上面LR的简介或者熟悉LR的形式，就可以看出这里的所得到的概率形式与LR及其相似，不同的是，概率形式中的z与原LR的形式wx+b不太一样。

　　仅仅上面的变形就说二者有关系稍微有点肤浅，那么究竟一样不一样呢？我们继续往下看：

　　根据概率模型那一章节，假设样本C1、C2均服从高斯分布，均值分别为μ1、μ2，方差分别为Σ1和Σ2，根据高斯分布的概率密度函数，那么带入上面z中的P(X|C1)和P(X|C2)，则有：

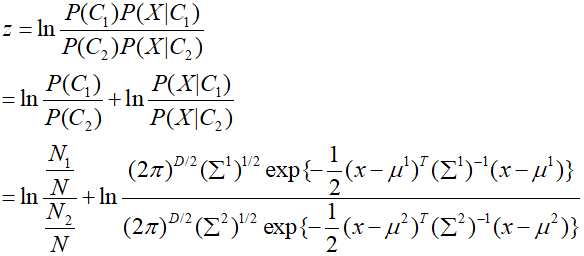
　　将上面的式子进行化简并展开：

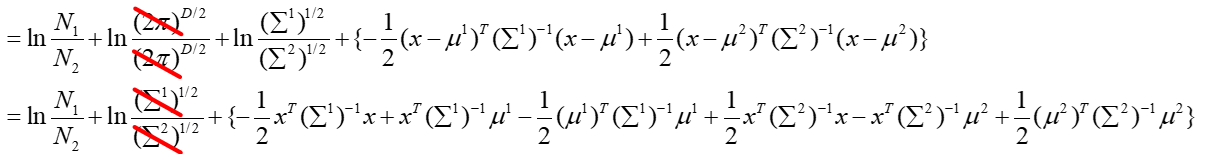
　　在概率模型中训练过程中，我们假设两个类别样本分布的方差Σ1和Σ2共用一个Σ，那么上面的式子可以进一步化简：

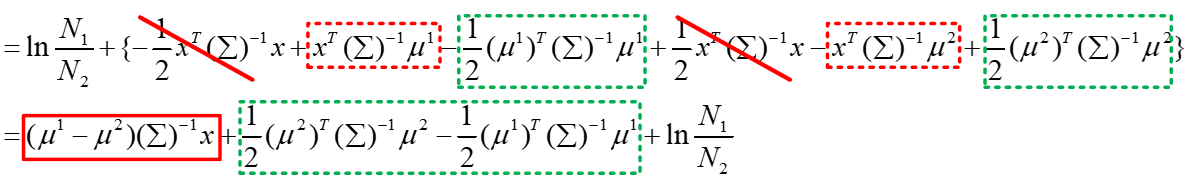
　　最终得到的z就是上面的式子，由于参数μ1、μ2、Σ是根据样本估计出来的参数，可以看做已知的，那么最终得到的z的形式如下：

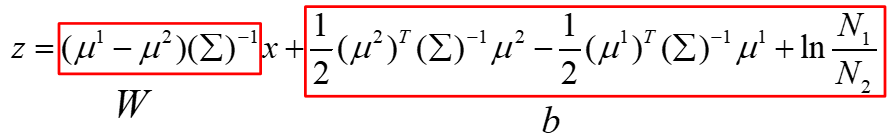
　　那么合并掉常数项，我们可以看到，z就变成了wx+b的形式，也就是说：

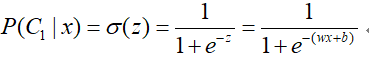
　　到这里我们就可以清楚地理解了概率生成模型与LR之间的联系，但虽然形式一样，但还是有区别的，到后面我们再进一步讨论。

3.LogisticRegression算法推导

　　根据上面的理论，我们希望通过训练数据，找到一组参数w、b，然后能够给定一个未知数据x，通过计算z=wx+b，在通过sigmoid函数，来对x进行正确预测。这里我们为了便于表示，先假设一下σ(z)为函数的形式，即：

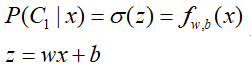
　　到这里完成了机器学习的三步走中的第一步：找出模型的形式a set of model。

　　那么在学习之前，我们需要找出一个衡量模型好坏的标准，即损失函数，到了第二步goodness of function：

　　我们希望所有的样本都能被正确分类，即所有样本累积概率最大，类比于概率生成模型，即：

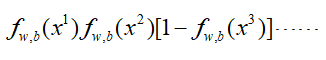
　　使上面这个式子最大，注意，这里x3为(1-f(x))，是因为上面我们所求的σ(z)=fw,b（x）是样本x属于Class1的概率，假设是二分类的情况，那么x属于Class2的概率为1-f(x)。

　　然后我们通过求加使得上式最大的一组w、b的参数就结束了，也就是：

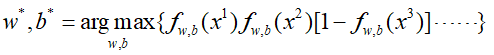
　　那么这个式子具体怎么求呢？同样用到梯度下降，但是上面直接求导不是很容易，要先对上面的式子进行一下转化，令：

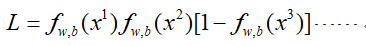
　　然后两边同取对数，并且由于梯度下降是求最小值，那么两边同取负号：

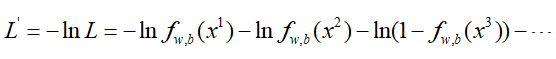
　　那么问题就变成了：

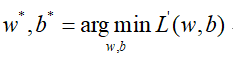
　　然而上面的式子还是有点不太直观，根据二分类的特性，label值在属于Class1时取1，在属于Class2时取0，那么：

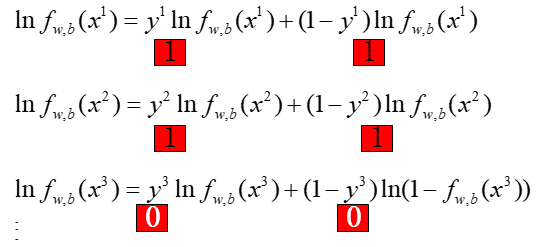
　　于是，L^'中的每一项我们都可以写成一个通用的形式，成为了：

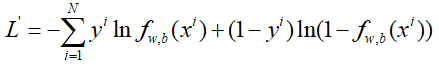
　　这就是LR的损失函数，也称之为交叉熵CrossEntropy，不过上面是0~1分布，形式上稍微有些不同，可以看成有两个分布，分别为：

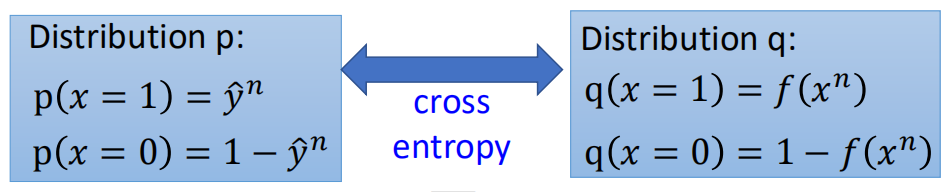
　　那么根据交叉熵的公式：

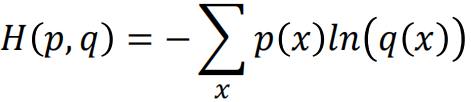
　　就得到了Lr的交叉损失函数。

　　接下来就是利用梯度下降对损失函数进行求解的过程了，也就是第三步：find the best function。

　　这个损失函数稍微有点复杂，涉及到链式求导法则，我们一块一块来求导数：

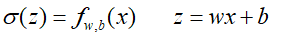
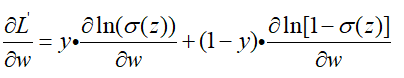
　　然后对两块复杂的地方进行求导：

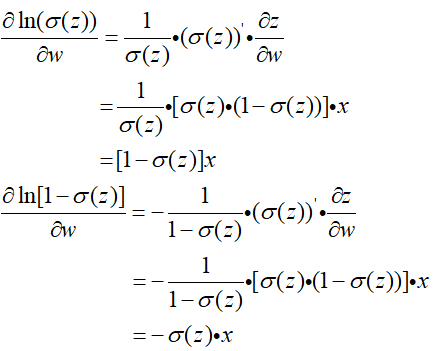
　　然后再带入上面的式子中进行整理：

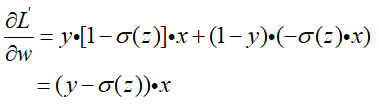
　　带上前面的加和，并带上负号，规范一下：

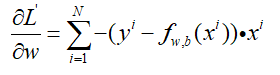
　　对b的求导也是一样的，不过在后面没有乘以x罢了，那么参数更新就是：

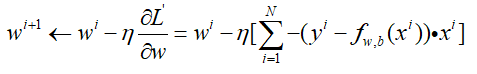
　　到这里是不是发现一个问题，仔细观察w的参数更新过程，对比Linear Regression的参数更新过程，可以看到参数的更新方程是一模一样的。

　　那为什么在LR中不能直接用均方误差MSE作为损失函数呢？

　　这里我们假设使用均方误差函数作为损失函数，那么损失函数为：

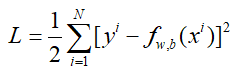
　　对w进行求导：

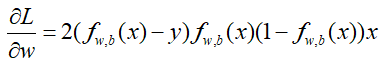
　　如果对于一个样本，该样本属于类别2，那么y=0，如果更新到一组参数w、b，计算得到fw,b(x)=1，那么此时预测该样本属于类别1，但带入梯度中发现此时梯度已经为0，参数将不再更新。

　　就像是下面这张图：

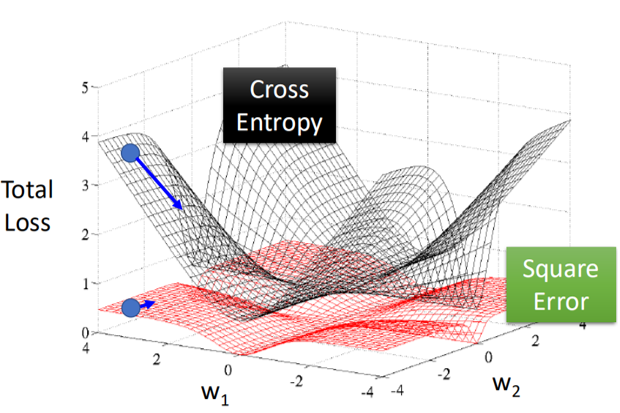
　　均方误差损失函数对于分类问题在距离Loss最小的地方也会很平坦，此时很可能陷入鞍点，无法继续更新，导致最终误差很大。

4.生成模型与判别模型

　　上面在从概率生成模型引入LR的过程中说到，虽然两者形式上是一样的，但其实还是有较大差别的。

　　根据二者的推导过程我们可以看到，在概率生成模型中，我们通过求解出样本的分布参数作为训练过程，即概率生成模型首先估计样本是个什么样的分布，然后再对这个分布的参数进行估计，换句话说，假设　　　　我们确定了样本所属的分布，那么这个分布里的数据都可以是训练数据，所多出来的数据并不影响最终的分布，相当于生成模型自己“脑补”生成出来了一些额外的数据，这种方式称之为生成模型。

　　而LR则是通过梯度下降的方式，直接求解出参数，这种方式称之为判别模型，其始终按照真实数据进行训练。

　　下面通过一个小例子来说明，假设有一组训练数据如下：

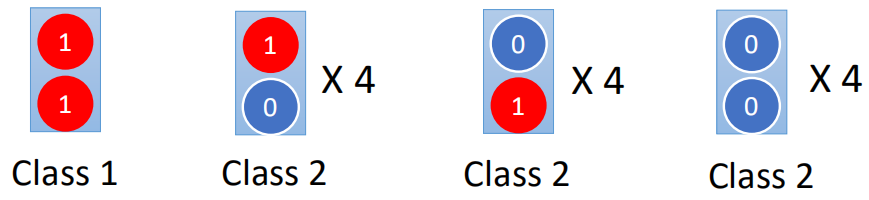
　　数据有两个维度，根据这样一组数据，对测试数据进行预测：

　　那么利用生成模型和判别模型分别预测的结果是什么呢？

　　首先看生成模型，利用朴素贝叶斯进行计算：

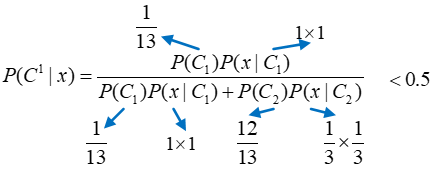
　　可以看出，利用生成模型计算得到的X属于Class2，而用判别模型因为X与唯一的属于Class1的训练样本一模一样，因此预测结果就是Class1。

　　从这里我们可以看出，生成模型在训练时会脑补出一些数据，可能出现一些训练集从来没出现的数据，比如（1,1）。

　　但通常由于判别模型解释性强，我们更倾向于相信判别模型，而生成模型是以概率假设为基础的，通常需要更少的训练数据，并且所得到的结果更具有鲁棒性。

5.多分类问题

　　上面所说的LogisticRegression是针对二分类问题的，对于多分类后面作为单独的一节进行论述，这里主要说与LR回归类似的多分类回归Softmax回归。

　　Softmax回归类似于LogisticRegression，将数据通过w、b线性叠加后，结合softmax函数，即可以实现将其表达为每种类别的概率的形式，softmax函数如下：

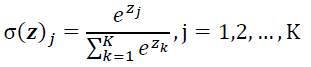
　　那么上面softmax回归的过程描述如下：

　　假设样本有3个类别C1、C2、C3，那么：

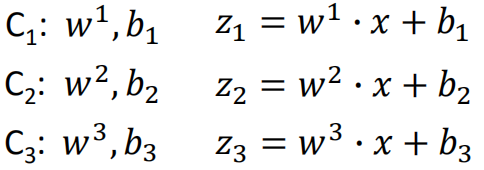
　　然后计算得到的z1、z2、z3通过softmax函数，计算各个类别的概率，过程如下：

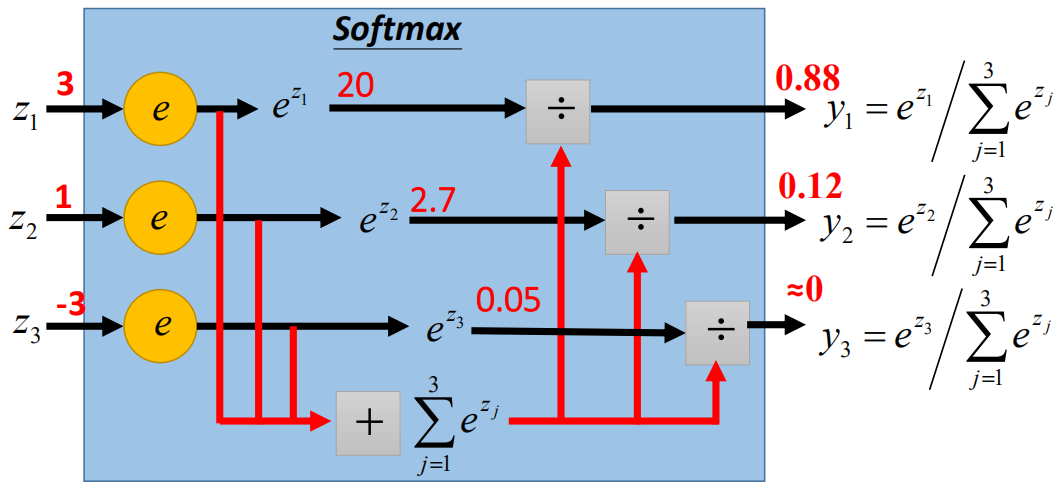
　　那么softmax的训练过程就可以类比LogisticRegression，过程如下：

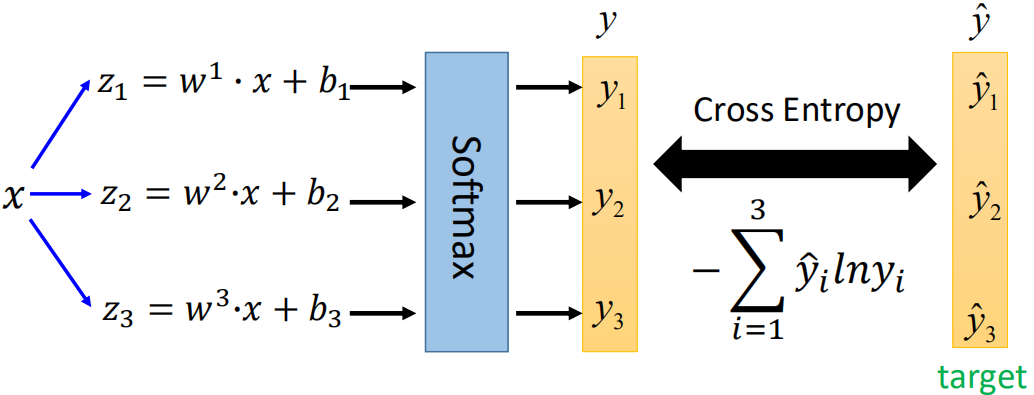
　　这里的交叉熵比LR的形式上更简单，因为可以将类别y表示成三维：Class1:[1,0,0]、Class2:[0,1,0]，Class3：[0,0,1]。具体过程就不再推导了。

6.LogisticRegression与神经网络联系

　　文章开头提到，LR回归与神经网络有一定的联系，具体有着什么样的关系呢？

　　LR对于一组二维的数据，我们通过w、b的线性加权后，再通过sigmoid的函数将其进行分类：

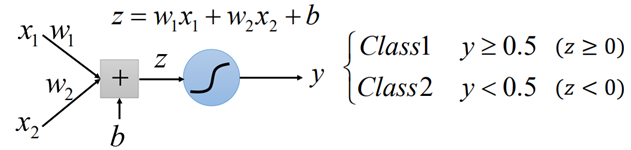
　　那今天如果有下图这样一组数据，我们是否能够找到一个线性模型，将这两类数据分开呢？

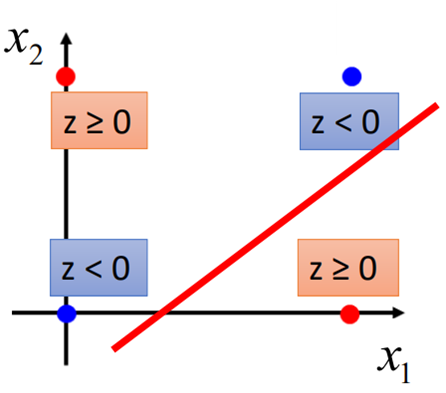
　　如果单纯直接对数据进行分类，可能线性模型将不能将其分开，这时，我们可能需要找一些方法，将数据进行转换和重构，然后再进行分类。

　　那如果我将上面的二维数据进行转换，两个维度分别表示该点距离（0,0）的距离和距离（1,1）的距离，那么左下角（0,0）的点可以转化为：

　　　　x1=0；（0,0）距离（0,0）的距离：

　　　　x2=√2；（0,0）距离（1,1）的距离；

　　那么点（0,0）就转换成为了（0，√2），同理（1,1）转换成为了（√2，0），（0,1）转换成为了（1，1），（1,0）转换成了（1，1），转换后的数据如图：

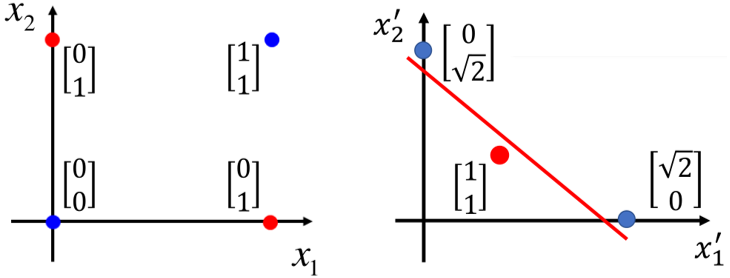
　　这样转换后就能通过一条直线将数据分开了，具体的转换方法有很多，比如SVM中的核函数、或者专业领域知识。

　　上面的过程就是特征转换后再经分类器对样本分类，假设上面这一组数据经过线性的加权，然后再经过sigmoid函数，对原始数据进行转换，然后再作为LR的输入在进行分类，其过程如图所示：

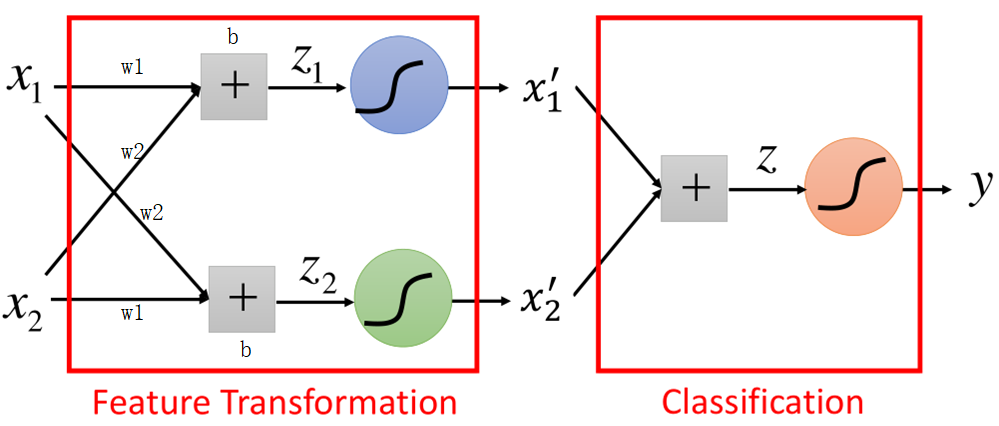
　　举个例子，比如w1=-2，w2=2，b=-1，四个点的都是二维的，每个维度转换后的如图所示：

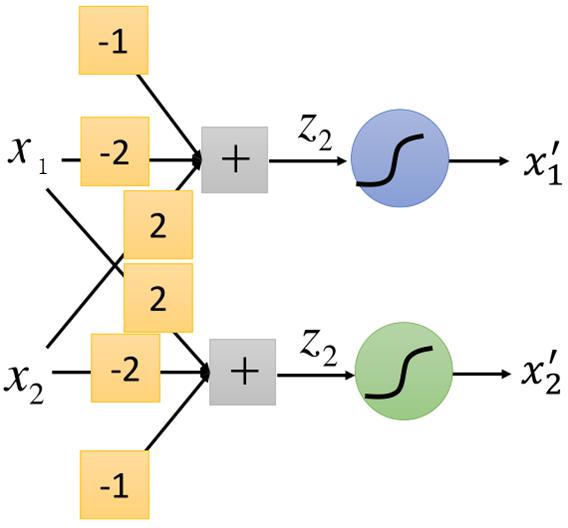
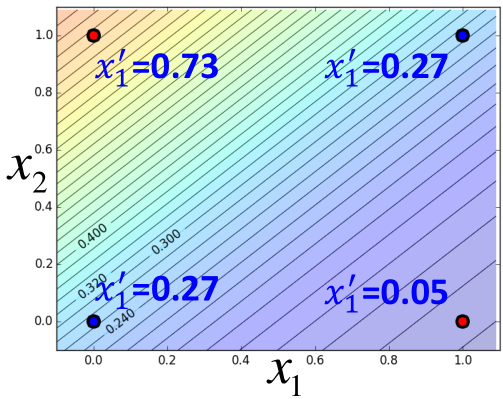
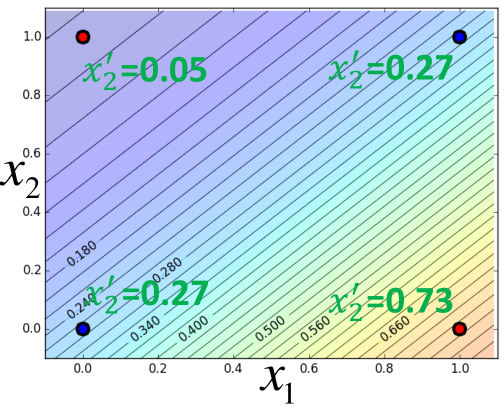
　　然后再将x1'，x2'作为输入，利用LogisticRegression进行分类，如图所示：

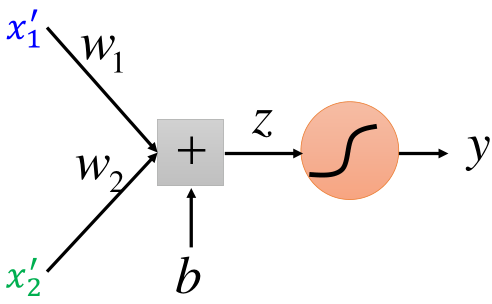
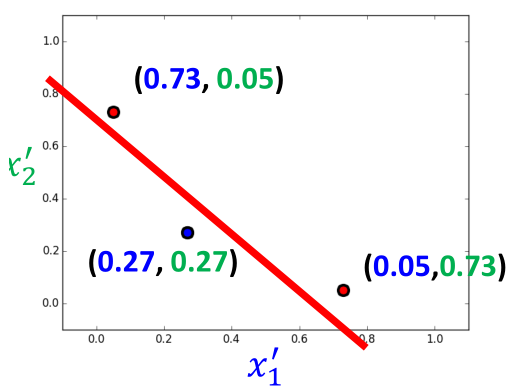
　　了解神经网络的应该到这里就可以看出来，上面的结构就是神经网络的结构，前半部分是特征提取部分，后半部分是分类的过程。如图所示：

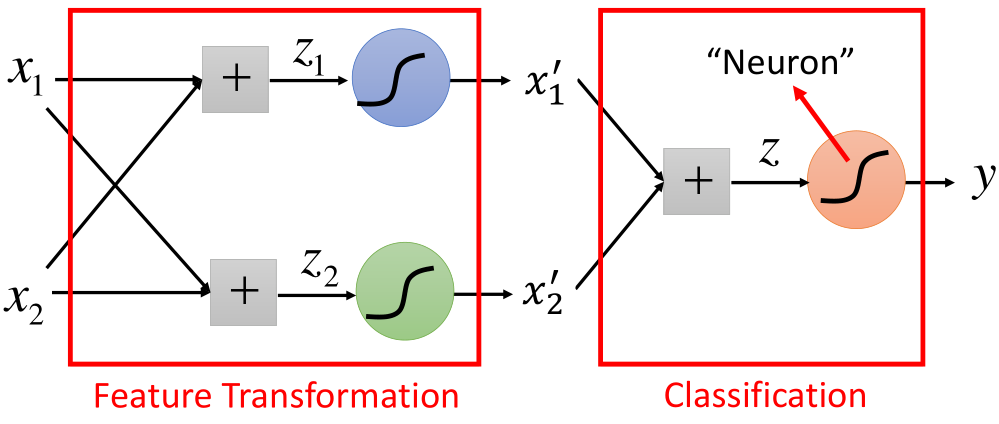
　　那么里边涉及到的参数w1、w2、b以及LR中的参数w3、w4、b2在神经网络中通过训练数据，可以一起被学习。

到这里LR的理论部分已经介绍完毕了，主要将其与概率生成模型和神经网络联系起来，下面主要对Lr涉及的主函数进行实现一下，然后利用数据集，采用Sklearn自带的LR方法进行实现。

7.LogisticRegression实现

　　数据来源于李宏毅老师的homework，数据下载地址：https://pan.baidu.com/s/1r07WmyRceBrXvEEKQ_3a-Q，提取码：t7pp。

　　数据描述的是不同属性人群的收入情况，feature是人物属性，label为收入情况，首先要对数据集进行转换，将非数值型数据都转换为数值型，然后数据分为训练集和测试集：

import numpy as npfrom sklearn.preprocessing import LabelEncoder

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

data = pd.read_csv('./train.csv', encoding='utf-8')

data = data[data['native_country'] != ' ?']

none_scalar = ['workclass', 'education', 'marital_status', 'occupation', 'relationship', 'race', 'sex', 'native_country']

label_encoder = LabelEncoder()

income = label_encoder.fit_transform(np.array(list(data['income'])))

data['income'] = income

onehot_encoded_dic = {}

for key in none_scalar:

    temp_data = np.array(list(data[key]))

    label_encoder = LabelEncoder()

    integer_encoded = label_encoder.fit_transform(temp_data)

    onehot_encoded_dic[key] = integer_encoded

feature_list = data.columns.to_list()

data_set = []

for i in range(len(data)):

    temp_vector = []

    for j in range(len(feature_list)):

        if feature_list[j] in onehot_encoded_dic.keys():

            temp_vector.extend(onehot_encoded_dic[feature_list[j]][i])

        else:

            temp_vector.append(data.iloc[i, j])

    data_set.append(temp_vector)

data_set = np.array(data_set)

np.random.shuffle(data_set)

trainX, testX, trainY, testY = train_test_split(data_set[:, :-1], data_set[:, -1], test_size=0.3)

　　然后先定义两个辅助函数，一个sigmoid函数，另一个是训练过程中用于将数据打散，便于利用batch_size梯度下降算法取数据：

def _shuffle(trainx, trainy):

    randomlist = np.arange(np.shape(trainx)[0])

    np.random.shuffle(randomlist)

    return trainx[randomlist], trainy[randomlist]

def sigmoid(z):

    res = 1/(1 + np.exp(-z))

    return np.clip(res, 1e-8, (1-(1e-8)))

　　接下来就是训练的主函数，因为lr算法比较简单，所以同训练部分写在一起：

def train(trainx, trainy):

    # 这里将b也放进了w中，便于求解，只需要求解w的梯度即可

    trainx = np.concatenate((np.ones((np.shape(trainx)[0], 1)), trainx), axis=1)

    epoch = 300

    batch_size = 32

    lr = 0.001

    w = np.zeros((np.shape(trainx)[1]))

    step_num = int(np.floor(len(trainx)/batch_size))

    cost_list = []

    for i in range(1, epoch):

        train_x, train_y = _shuffle(trainx, trainy)

        total_loss = 0.0

        for j in range(1, step_num):

            x = train_x[j*batch_size:(j+1)*batch_size, :]

            y = train_y[j*batch_size:(j+1)*batch_size]

            y_ = sigmoid(np.dot(x, w))

            loss = np.squeeze(y_) - y

            cross_entropy = -1 * (np.dot(y, np.log(y_)) + np.dot((1-y), np.log(1-y_)))/len(x)

            grad = np.dot(x.T, loss)/len(x)

            w = w - lr * grad

            total_loss += cross_entropy

        cost_list.append(total_loss)

        print("epoch:", i)

    return w, cost_list

　　最后，写一个计算错误率的函数，用于比较模型预测结果与原数据的差距有多大：

def evaluation2(X, Y, w):

    X = np.concatenate((np.ones((np.shape(X)[0], 1)), X), axis=1)

    y = np.dot(X, w)

    y = np.array([1 if example > 0.5 else 0 for example in list(y)])

    error_count = 0

    for i in range(len(y)):

        if y[i] != Y[i]:

            error_count += 1

    error_rate = error_count/len(y)

    return error_rate

　　然后，就可以直接进行训练了：

w, cost_list = train(trainX, trainY)

error_rate2 = evaluation2(trainX, trainY, w)

print('训练集上的错误率为：', error_rate2)

print('测试集上的错误率为：', evaluation2(testX, testY, w))

训练集上的错误率为： 0.217566118656183

测试集上的错误率为： 0.2140921409214092

　　然后是用sklearn中LogisticRegression方法对上面的过程进行实现，其实很简单，这里就建立一个默认参数模型，稍后说明LogisticRegression中各个参数：

model = LogisticRegression()

model.fit(trainX, trainY)

print('训练集上的错误率为：', model.score(trainX, trainY))

print('训练集上的错误率为：', model.score(testX, testY))

训练集上的错误率为： 0.7915475339528234

训练集上的错误率为： 0.7883051907442151

　　下面就说一下LogisticRegression中的参数：LR的参数官方文档https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html

“max_iter”:最大迭代次数；

“penalty”：惩罚项，即正则项，默认为L2正则，可选有L1正则，一般来说L2正则化就够了，但如果还是会过拟合，可选择L1正则，或者样本特征维度较大，希望归零一些不重要的特征，也可以选择L1正则；

“solver”：优化方法，默认为‘lgfgs’,即一种拟牛顿法，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数；此外还有：

　　　　 ‘liblinear’，坐标轴梯度下降方法来优化损失函数；数据量较小时可以选择这种方法；

　　　　 ‘newton-cg’:也是一种牛顿法中的一种；

　　　　 ‘sag’:随机平均梯度下降，是‘sgd’的一种随机梯度下降算法的加速版本，sag其实每次计算时，利用了两个梯度的值，一个是前一次迭代的梯度值，另一个是新的梯度值。当然这两个梯度值都只是随机选取一个样本来计算。当数据量很大时可以选择这种方法；

　　　　这里要说明的是，penalty选择了l1后，在solver中就只能用liblinear这个优化方法了，因为L1正则化没有连续导数。

　　　　 solver的官网文档如下：

　　　　总结而言，liblinear支持L1和L2，只支持OvR做多分类，“lbfgs”, “sag” “newton-cg”只支持L2，支持OvR和MvM做多分类。

multi-class：该参数是分类的方式，有两个值可以选择：‘ovr’和‘multinomial’，默认为‘ovr’，

　　　　　　‘ovr’即一对多的分类，后面会对多分类做一个总结说到这种方法，具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元逻辑回归，得到第K类的分类模型。

　　　　　　‘mvm’：如果模型有T类，我们每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类。

class-weight:样本的类别权重，在分类模型中，经常会遇到两种问题，第一种是误分类的代价很大，就比如合法用户和非法用户，宁愿将合法用户错分到非法用户，然后再通过人工甄别，好过将非法用户误分到合法用户类别中，这时可以适当提高非法用户的权重，class_weight={0:0.9, 1: 0.1}.

　　　　　　另一种是样本严重失衡，比如病例检测中，患病人数远小于不患病人数，假设有10000人检查，患病人数只有0.5%，若不考虑权重，那么准确率也有99.5%，但这样的模型显然没有意义，这时可以选择balanced，让类库自动提升患病样本的权重。

sample_weight:对于样本的不均衡，一种方法是上面class_weight设置balanced，另一种就是在fit的时候通过设置每个样本的权重来调整样本权重，在scikit-learn做逻辑回归时，如果上面两种方法都用到了，那么样本的真正权重是class_weight*sample_weight。

dual: 对偶方法还是原始方法，默认为False，对偶方法只在求解线性多核的L2正则惩罚中使用，当样本数量>样本特征的时候，dual通常设置为False。

　　LogisticRegression中的主要参数就是这些，还有一些其他的参数可以看官方文档中说明。

　　对上面的数据集，调整一下使用L1惩罚和solver改为liblinear，正确率略有提升最终结果为：

训练集上的错误率为： 0.8259471050750536
测试集上的错误率为： 0.8217636022514071

另外，最近看到一个问题：“比较一下LR模型和GBDT的差别，什么情况下GBDT不如LR模型？”在这里顺便做个总结：

GBDT与LR的区别：

①LR是线性模型，而GBDT是多个弱分类器叠加一起的非线性模型；因此有时为了增强模型的非线性表达能力，通常使用LR模型时，需要做大量的特征工程的工作；

②LR是单模型，而GBDT是集成模型，对于低噪声的数据，GBDT往往比LR的效果更好；

③LR采用梯度下降的等方式进行训练，往往需要对特征进行归一化处理，而GBDT不需要做特征的归一化。

GBDT不如LR的地方：

①LR的解释能力更强，当对模型需要解释时，GBDT往往更加“黑盒”，因为不可能去解释每一棵树，而LR的特征权重能够更直观的看出每个特征的贡献大小，因此LR更具有说服力和营销策略；

②LR的大规模并行训练已经非常成熟，模型迭代和训练速度很快，而GBDT是一种串行的方式，在数据量较大时训练速度较慢；

③对于高维稀疏矩阵，GBDT往往很容易过拟合，因为这些无用信息，在进行决策树训练时，会导致树变得很深，因此会容易过拟合，而LR在训练时可以加入正则化，从而降低特征的权重（L2正则），或者删除不重要的特征（L1正则），从而防止过拟合。

有关逻辑回归的内容到这里就结束了，练习的时候这里说了LR与神经网络的关系，后面就初步回顾一下神经网络有关内容。