Proximal Algorithms 2 Properties

可分和
基本的运算
不动点 fixed points
Moreau decomposition

可分和

如果$f$可分为俩个变量:$f(x, y)=\varphi(x) + \psi(y)$, 于是:

如果$f$是完全可分的，即$f(x) = \sum_{i=1}^n f_i (x_i)$:

\[(\mathbf{prox}_f(v))_i = \mathbf{prox}_{f_i}(v_i)
\]

这个性质在并行算法的设计中非常有用。

基本的运算

如果$f(x) = \alpha \varphi (x) + b$, $\alpha > 0$:

\[\mathbf{prox}_{\lambda f} (v) = \mathbf{prox}_{\alpha \lambda \varphi} (v)
\]

如果$f(x) = \varphi (\alpha x +b)$, $\alpha \ne 0$:

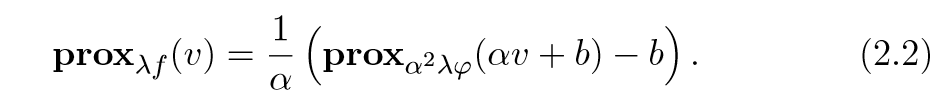
证：

\[\begin{array}{ll}
\mathbf{prox}_{\lambda f}(v) &= \mathrm{argmin}_x \varphi(\alpha x+b) +\frac{1}{2\lambda}\|x-v\|_2^2 \\
&= \mathrm{argmin}_x \varphi(z) + \frac{1}{2\lambda}\|(z-b)/\alpha -v\|_2^2 \\
&= \mathrm{argmin}_x \varphi(z) + \frac{1}{2\lambda \alpha^2}\|z-b -\alpha v\|_2^2 \\
&= \frac{1}{\alpha} (\mathbf{prox}_{\alpha^2 \lambda \varphi}(\alpha v + b) - b)
\end{array}
\]

其中$z=\alpha x+b$,证毕.

如果$f(x) = \varphi(Qx)$，且$Q$为正交矩阵:

\[\mathbf{prox}_{\lambda f} (v) = Q^T \mathbf{prox}_{\lambda \varphi}(Qv)
\]

如果$f(x) = \varphi(x) + a^Tx + b$，则:

\[\mathbf{prox}_{\lambda f}(v) = \mathbf{prox}_{\lambda \varphi} (v-\lambda a)
\]

证:

\[\begin{array}{ll}
\mathbf{prox}_{\lambda f}(v) &= \mathrm{argmin}_x \varphi (x) + a^Tx + b + \frac{1}{2\lambda} \|x-v\|_2^2 \\
&= \mathrm{argmin}_x \varphi(x) +\frac{1}{2 \lambda} (x^Tx -2v^Tx+2\lambda a^Tx)+c \\
&= \mathrm{argmin}_x \varphi(x) + \frac{1}{2 \lambda} \|x-(v-\lambda a)\|_2^2 \\
&= \mathbf{prox}_{\lambda \varphi}(v-\lambda a)
\end{array}
\]

其中$c$为与$x$无关的项.

如果$f(x) = \varphi(x) + (\rho/2) \|x -a \|_2^2$, 则:

\[\mathbf{prox}_{\lambda f} (v) = \mathbf{prox}_{\widetilde{\lambda}\varphi}\big((\widetilde{\lambda}/\lambda)v + (\rho \widetilde{\lambda})a \big)
\]

其中$\widetilde{\lambda} = \lambda / (1+\lambda \rho)$，证明方法和上面是类似的，重新组合二次项就可以了.

不动点 fixed points

点$x^*$最小化$f$当且仅当:

\[x^* = \mathbf{prox}_f (x^*)
\]

这说明，$x^*$是$\mathbf{prox}_f$的一个不动点，这个性质对于$\lambda f$也是成立的.

压缩映射的定义:

考虑映射$T: (X, \rho) \rightarrow (X, \rho)$. 如果存在$0 < a < 1$使得对任意的$x, y \in X$有:

\[\rho (Tx, Ty) < a \rho(x, y)
\]

则称函数$T$是$(X, \rho)$到自身的压缩映射.

如果$\mathbf{prox}_f$是一个压缩映射，那么显然，如果我们想要找出最小化$f$的$x^*$，可以用下式迭代：

\[x^{n+1} = \mathbf{prox}_f(x^n) \rightarrow x^*
\]

比如$\mathbf{prox}_f$满足$L<1$的Lipschitz条件.

近端算子有这个性质:

这儿有关于这块内容的讨论.

$x = \mathbf{prox}_f(v) \Leftrightarrow v-x \in \partial f(x)$，其中$\partial$表示次梯度.

设$u_1 = \mathbf{prox}_f(x), u_2 = \mathbf{prox}_f(y)$,则:

\[x - u_1 \in \partial f(u_1) \\
y - u_2 \in \partial f(u_2)
\]

因为$f$是凸函数，所以$\partial f$是单调增函数:

\[<x - u_1 - (y-u_2), u_1-u_2> \ge 0 \\
\Rightarrow \|u_1 - u_2\|_2^2 \le (x-y)^T(u_1-u_2)
\]

上面的单调增函数，翻译的估计不对，主要是我对这方面的只是也不了解，原文用的是monotone mapping, 我们来看凸函数$f(x)$:

\[f(y) \ge f(x) + \partial f(x)^T (y-x) \\
f(x) \ge f(y) + \partial f(y)^T(x-y)
\]

相加即得：

\[(\partial f(x) - \partial f(y))^T (x-y) \ge 0
\]

还有严格凸的情况下有个特殊情况，这个怎么证明啊...而且，似乎在不是严格凸的，利用上面的迭代公式也是能够收敛到不动点的，可似乎不满足不动点定理啊.

而且作者将这个与平均算子(averaged operators)联系起来:

\[T = (1-\alpha)I+\alpha N, \alpha \in (0, 1)
\]

以及迭代公式:

\[x^{k+1}:=(1-\alpha ) x^k + \alpha N
\]

Moreau decomposition

有以下事实成立:

以下的证明是属于

沿用其符号，令（注意是$\inf$不是$\mathrm{argmin}$）

\[f_{\mu}(x) = \inf_y \{f(y) + \frac{1}{\mu} \|x-y\|_2^2\}
\]

我们可以其改写为:

注意$-\sup A=\inf -A$

假设$f$是凸函数且可微的,那么:

\[f^*(y)={x^*}^T \nabla f(x^*) - f(x^*)
\]

其中，$x$满足:$y=\nabla f(x^*)$。于是(注意$\nabla f(x^*)=y$, 且上式是关于$y$求导):

\[\nabla f^* (y) = x^*
\]

这就是$\nabla f_{\mu} (x)$的由来.

我们再来看其对偶表示:

其拉格朗日对偶表示为：

如果满足强对偶条件:

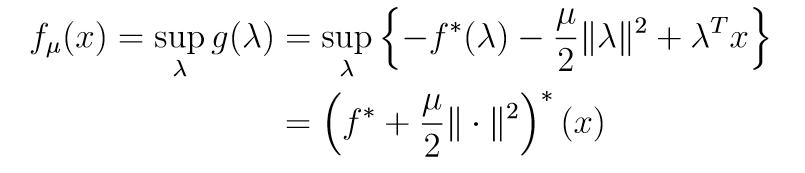
所以:

\[f_{\mu}(x) = \frac{1}{2 \mu} \|x\|^2-\frac{1}{\mu}(\mu f+\frac{1}{2}\|\cdot\|^2)^*(x) =(f^* + \frac{\mu}{2} \|\cdot\|^2)^*(x) \\
\Rightarrow \frac{1}{2}\|x\|^2= ( \mu f + \frac{1}{2}\|\cdot\|^2)^*(x)+\mu (f^*+\frac{\mu}{2}\|\cdot\|^2)^*(x) \\
\Rightarrow x= \mathbf{prox}_{\mu f}(x) + \mu\mathbf{prox}_{\frac{1}{\mu}f^*}(\frac{x}{\mu})=x = \mathbf{prox}_{\mu f}(x) + \mathbf{prox}_{(\mu f)^*}(x)
\]

最后一步的结果通过对上式俩边求导得到的，不知道对不对，但是$\mu=1$的时候，下式是一定成立的:

\[x = \mathbf{prox}_f(x) + \mathbf{prox}_{f^*}(x)
\]