Histogram Processing

HISTOGRAM EQUALIZATION
- 代码示例
HISTOGRAM MATCHING (SPECIFICATION)
其它

Gonzalez R. C. and Woods R. E. Digital Image Processing (Forth Edition).

令$r_k, k = 0, 1,2, \cdots, L-1$ 表示图片密度值为$k$,

\[h(r_k) = n_k, \: k = 0, 1, \cdots, L-1,
\]

整个图片$f(x, y)$中密度值为$r_k$的pixel的数量, 定义概率

\[p(r_k) = \frac{h(r_k)}{MN} = \frac{n_k}{MN},
\]

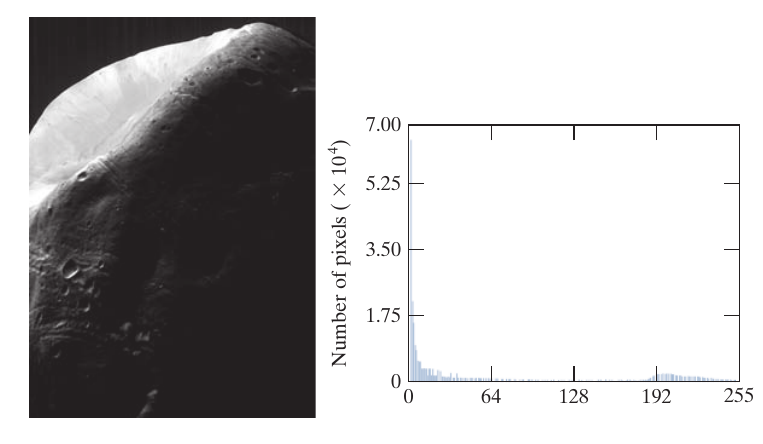
其中$M, N$分别表示图片的高和宽(注意, 如果是多通道的图, 则应该$CMN$). 下图即为例子, 统计了$r_k$的分布.

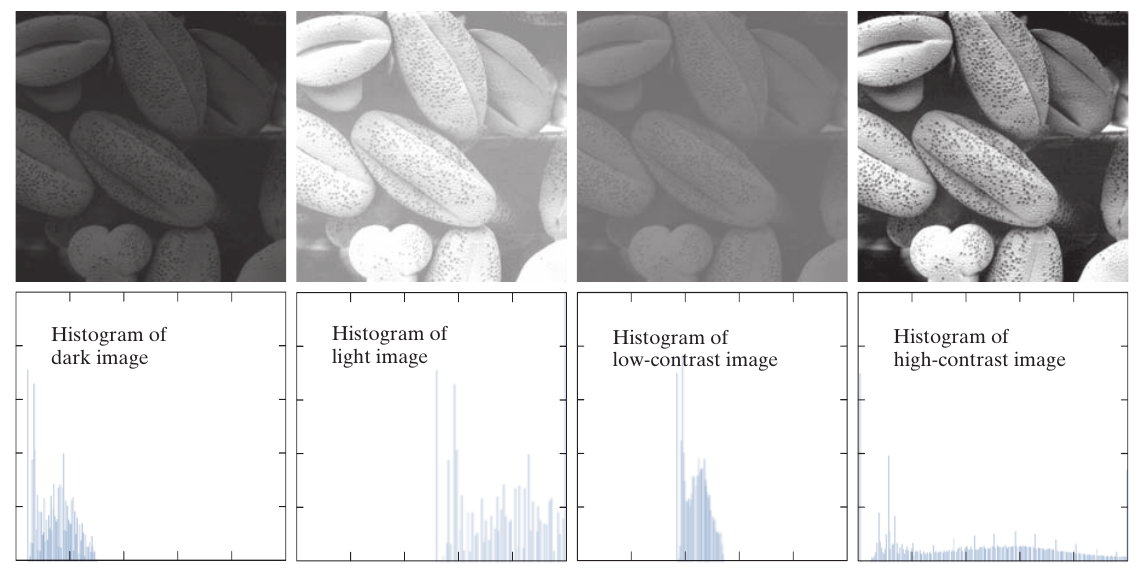
HISTOGRAM EQUALIZATION

上面的四幅图, $r_k$呈现了不同的分布, 其中第四幅图, 拥有最佳的对比度, 可以发现其$r_k$的分布近似一个均匀分布, histogram equalization就是这样一种方法, 寻找一个变换

\[s = T(r), \quad 0 \le r \le L-1,
\]

使得$s$的分布近似满足一个均匀分布.

当然了, 这种分布显然不能破坏图片结构, 需要满足以下条件:

$T(r)$在$0\le r \le L-1$熵是一个单调函数;
$0 \le T(r) \le L-1, \quad \forall 0 \le r \le L-1$.

我们首先把$r$看成连续的, 且假设$p_r(r)$是一个连续的密度函数, 则定义

\[s = T(r) = (L-1) \int_0^r p_r(w) \mathrm{d} w.
\]

显然$\int_0^r p_r(w) \mathrm{d}w$单调, 故$T(r)$也是单调的, 又$0\le \int_0^r p_r(w) \mathrm{d}w \le 1$, 故第二个条件也是满足的.

既然$u = \int_0^r p_r(w) \mathrm{d}w$是满足均匀分布的随机变量($[0, 1]$), 故

\[s \sim U[0, L-1].
\]

即严格来说, 如果考虑连续的情况, 那么这种变换$T$一定能够得到我们所希望的最佳对比度.

将上述过程转换为离散的情况, 即

\[s_k = T(r_k) = (L - 1) \sum_{j=0}^k p_r (r_j), \: k=0,1,\cdots, L-1.
\]

为什么这种情况不能保证$s_k$满足均匀分布, 因为$s_k$可能是小数, 在图片中需要经过四舍五入操作, 就导致了不平衡.

代码示例

import cv2

import matplotlib.pyplot as plt

import numpy as np

# 加载图片

pollen = cv2.imread("./pics/pollen.png")

pollen.shape # (377, 376, 3) 由于是截的图, 所以是3通道的

pollen = cv2.cvtColor(pollen, cv2.COLOR_BGR2GRAY) # 先转成灰度图

pollen.shape # (377, 376)

plt.imshow(pollen, cmap='gray')

# 来看一下r的分布

hist = cv2.calcHist([pollen], [0], None, [256], (0, 255)).squeeze()

plt.bar(x=np.arange(256), height=hist)

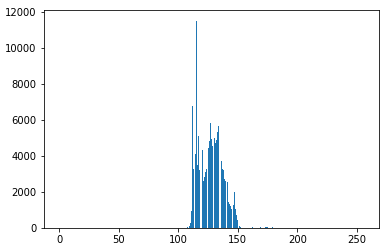
# 自己的实现 img 是灰度图, 且 0, 1, ..., 255

def equalizeHist(img):

    m, n = img.shape

    hist = cv2.calcHist([img], [0], None, [256], (0, 255)).squeeze() / (m * n)

    links = dict()

    cum_sum = 0

    for r in range(256):

        cum_sum += hist[r]

        links[r] = round(cum_sum * 255)

    img2 = img.copy()

    for i in range(m):

        for j in range(n):

            r = img[i, j].item()

            img2[i, j] = links[r]

    return np.array(img2)

pollen2 = equalizeHist(pollen)

plt.imshow(pollen2, cmap='gray')

hist = cv2.calcHist([pollen2], [0], None, [256], (0, 255)).squeeze()

plt.bar(x=np.arange(256), height=hist)

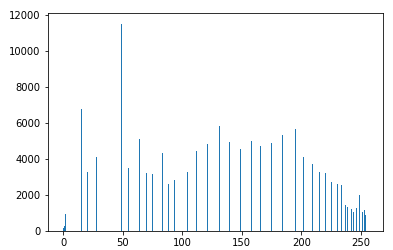
# cv2 官方实现

pollen3 = cv2.equalizeHist(pollen)

plt.imshow(pollen3, cmap='gray')

hist = cv2.calcHist([pollen3], [0], None, [256], (0, 255)).squeeze()

plt.bar(x=np.arange(256), height=hist)

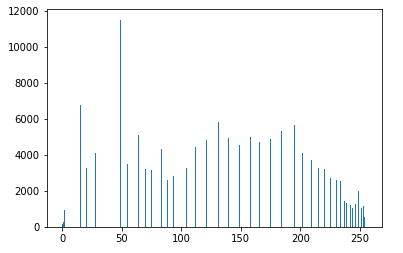
HISTOGRAM MATCHING (SPECIFICATION)

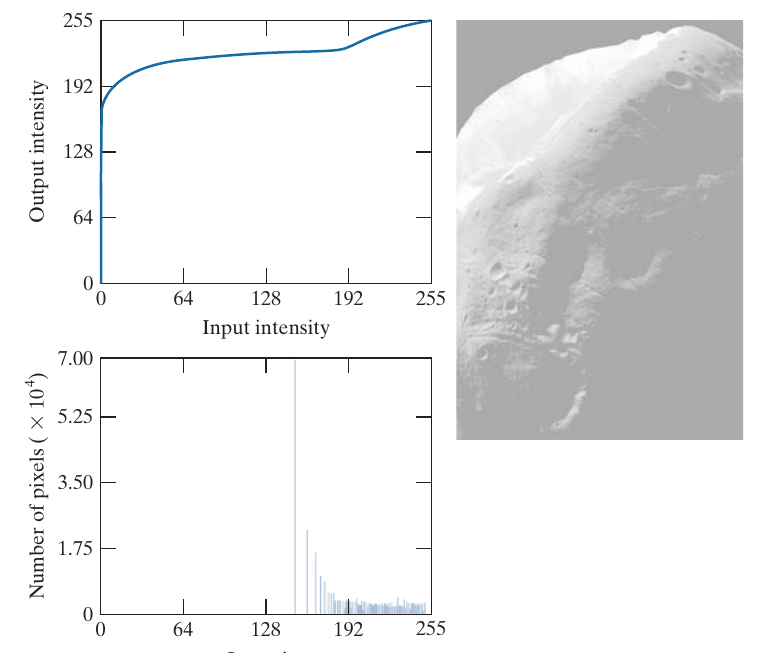
正如上面所说的, equalize只在连续的情况下是能够保证转换后的分布是均匀的, 当离散的时候, 实际上, 当分布特别聚集的时候, 出现的分布会与均匀相差甚远. 如下面的月球的表面图, 由于其分布集中在0附近, 导致变换后的图形并不能够很好的增加对比度(虽然能看清点).

此时, 我们可以预先指定一个分布$p_z$, 回顾:

\[s = T(r) = (L-1) \int_0^r p_r (w) \mathrm{d} w,
\]

我们将$s \rightarrow z$:

\[s = G(z) = (L-1) \int_0^z p_z (v) \mathrm{d} v,
\]

$T(r) = s =G(z)$, 既然在连续的情况下$s$是均匀的, 故

\[z = G^{-1} T(r),
\]

当然需要一个额外的假设$G$是可逆的. 如此, 我们变把$r$转换成了我们期待的分布$z$.

那么在离散的情况下, 处理流程如下:

通过

\[T(r_k), \: k = 0, 1, \cdots, L-1,
\]

建立字典

\[d_{rs}=\{r_k:\mathrm{round}(T(r_k))\}.
\]
通过

\[G(z_k), \: k = 0, 1, \cdots, L-1,
\]

对于每一个$s_k$, 从$z_j, j=0,1,\cdots, L-1$中找到一个$z_j$使得$G(z_j)$与$s_k$最接近, 并建立字典

\[d_{sz} = \{s_k:z_j\}.
\]

$r \rightarrow z$:

\[z = d_{sz}[d_{rs}[r]].
\]

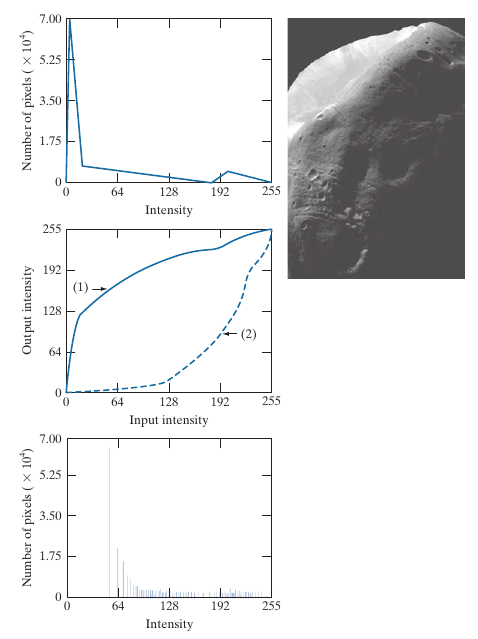
在实际中, 一般取原图$r$分布一个光滑近似, 如下图所示(个人觉得, 此处核密度函数估计大有可为):

其它

有些时候, 我们只需要对一部分的区域进行上述的处理, 就是LOCAL HISTOGRAM PROCESSING.

另外, 可以用一些统计信息来处理, 比如常见的矩

\[\mu_n = \sum_{i=0}^{L-1} (r_i-m)^n p(r_i), \\
m = \sum_{i=0}^{L-1}r_i p(r_i),
\]

这里$m$是均值. 常用的二阶矩, 方差:

\[\sigma^2 = \sum_{i=0}^{L-1} (r_i - m)^2 p(r_i),
\]

是图片对比度的一种衡量的手段.

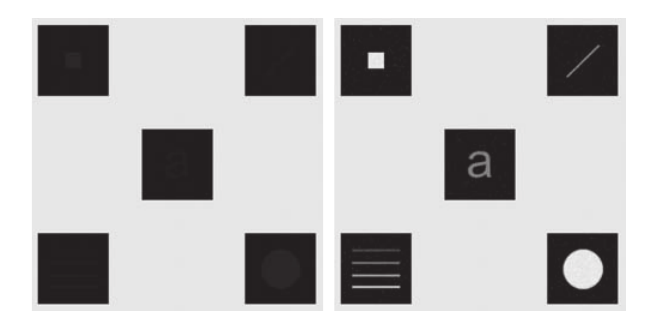
对于以$(x, y)$为中心的区域, 也可以各自定义其矩$\mu_{S_{xy}}$. 下图就是通过区域的一阶矩和二阶矩的信息来让黑色部分的对比度增加.