势能分析（splay分析）

定义

第\(x\)次操作后，势能为\(\phi(x)\)，该操作实际复杂度\(c(x)\)，均摊复杂度\(a(x)\)。

定义\(a(x)=c(x)+\phi(x)-\phi(x-1)\)。

那么总复杂度为$\phi(n)-\phi(0)+\sum c(x) $。

简单应用

Q：对于一个初始为0的二进制数，每次+1，求n次操作复杂度。

A：定义\(\phi(x)\)为\(i\)次操作后1的个数，对于一次+1 ，1个0->1，x个1->0，那么\(a(x)= (1+x) + (1-x)=2\)，则总复杂度\(o(n)\)，常数2。

splay分析

定义x节点的势能为\(\chi(x)=log(size(x))\)（size表示子树大小）。

那么\(\phi(n)-\phi(0) \leq n log(n)\)。

双旋分三种情况（y=fa[x]，z=fa[y]）：

1. y为根
2. x,y,z同一条直线
3. x,y,z不为同一条直线

（弄错了不想改...祖孙关系以图为准）

对于1：

\[c(x)=1+ \chi(x^{'})+\chi(y^{'})-\chi(x)-\chi(y)=1+\chi(y^{'})-\chi(y)
\]

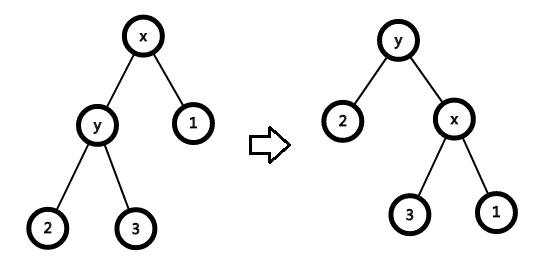
对于2：

\[c(x)=2+\chi(x^{'})+\chi(y^{'})+\chi(z^{'})-\chi(x)-\chi(y)-\chi(z)
\]

\[c(x)=2+\chi(x^{'})+\chi(y^{'})-\chi(y)-\chi(z) \leq 2+\chi(z^{'})+\chi(x^{'})-2\chi(z)
\]

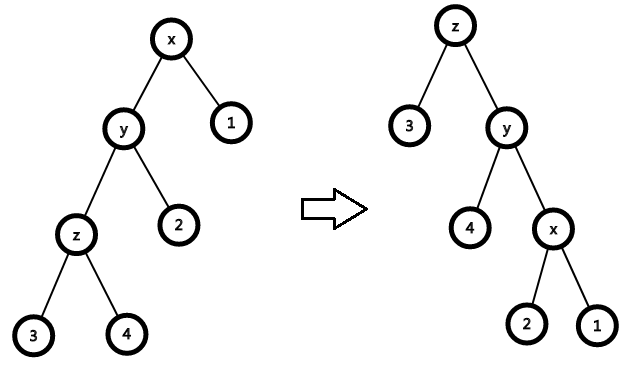
而

\[\chi(x^{'})+\chi(z)-2\chi(z^{'})=log({(size(2+1)+1)\times（size(3+4)+1）\over {(3+size(3+4+2+1))}^2}) \leq log( {1 \over 4})=-2
\]

那么

\(c(x)\leq 2+\chi(z^{'})+\chi(x^{'})-2\chi(z) \leq 3(\chi(z^{'})-\chi(z))\)

对于3：

\[c(x)=2+\chi(x^{'})+\chi(y^{'})+\chi(z^{'})-\chi(x)-\chi(y)-\chi(z)
\]

\[c(x)=2+\chi(x^{'})+\chi(y^{'})-\chi(y)-\chi(z) \leq 2+\chi(x^{'})+\chi(y^{'})-2\chi(z)
\]

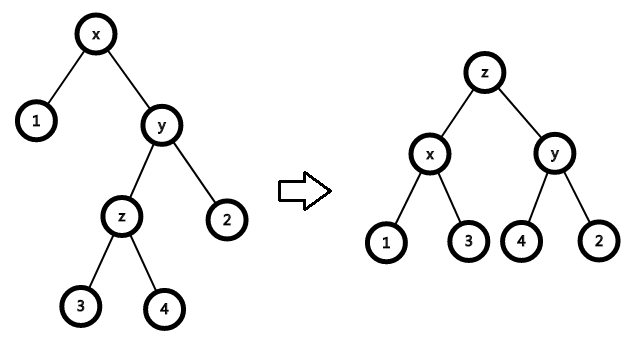
而

\[2\chi(z^{'})-\chi(x^{'})-\chi(y^{'})=log({(size(1+3+4+2)+3)^2 \over{(size(1+3)+1) \times (size(4+2)+1)}}) \geq 2
\]

故

\[c(x) \leq 2(\chi(z^{'})-\chi(z))
\]

综上

可以把\((\chi(z^{'})-\chi(z))\)的常数都看为3。

一次splay复杂度为\(3 (\chi(root)-\chi(z))+1 \leq 3 log(n)+1\)。

然后这个还要乘上rotate的常数。

不过在实际应用下，可以认为常数为8。