Trees Made to Order——Catalan数和递归

Trees Made to Order

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 7155		Accepted: 4094

Description

We can number binary trees using the following scheme: 
The empty tree is numbered 0. 
The single-node tree is numbered 1. 
All binary trees having m nodes have numbers less than all those having m+1 nodes. 
Any binary tree having m nodes with left and right subtrees L and R is numbered n such that all trees having m nodes numbered > n have either Left subtrees numbered higher than L, or A left subtree = L and a right subtree numbered higher than R.

The first 10 binary trees and tree number 20 in this sequence are shown below: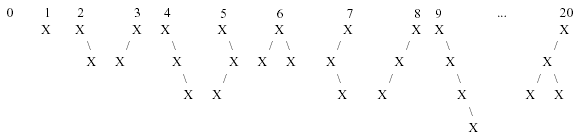 

Your job for this problem is to output a binary tree when given its order number. 

Input

Input consists of multiple problem instances. Each instance consists of a single integer n, where 1 <= n <= 500,000,000. A value of n = 0 terminates input. (Note that this means you will never have to output the empty tree.)

Output

For each problem instance, you should output one line containing the tree corresponding to the order number for that instance. To print out the tree, use the following scheme:

A tree with no children should be output as X. 
A tree with left and right subtrees L and R should be output as (L’)X(R’), where L’ and R’ are the representations of L and R. 
If L is empty, just output X(R’). 
If R is empty, just output (L’)X. 

Sample Input

1 20 31117532 0

Sample Output

X ((X)X(X))X (X(X(((X(X))X(X))X(X))))X(((X((X)X((X)X)))X)X)

题目大意：根据下面的规则给一棵二叉树编号：

规则1：如果二叉树为空，则编号为0；

规则2：如果二叉树只有一个节点，则编号为1；

规则3：所有含有m个节点的二叉树的编号小于所有含有m+1个节点的二叉树的编号；

规则4：如果一棵含有m个节点的二叉树（左子树为L，右子树为R）的编号为n，要想其它含有m个节点的二叉树的编号如果大于n，则需要满足两个条件中的任意一个：1、左子树的编号大于L的编号；2、左子树的编号等于L的编号，但是右子树的编号大于R的编号。

解题方法：卡特兰数列（Catalan）+递归

Catalan数列简介：令Catalan(0)=1，Catalan(1)=1，Catalan数列满足地推公式：

Catalan(n)=Catalan(0)*Catalan(n-1)+Catalan(1)*Catalan(n-2)+...+Catalan(n-1)*Catalan(0)，其中n>=2;

catalan数在这道题的理解，简单的来说就是一个节点数为n的二叉树的形态的个数，即为划分的个数

详情移步：Catalan卡塔兰数

假设f(n)表示n个节点的二叉树的所有顺序，由于左子树和右子树的顺序是相互独立的，假设0<=i<=n：表示左子树有i个节点，则右子树有n-i-1个节点（要除去根节点），则含有n个节点的二叉树，当左子树含有i个节点时，二叉树的节点顺序树为：f(i)*f(n-i-1)，i从0到n-1 ，然后累加就可以求出所有f(n). 这就是一点典型的Catalan数列问题。

解题思路：

split(NodeNum,order)是用于打印问题的解的函数，其中NodeNum为当前树的结点数，order为当前树在 节点数为NodeNum的所有树中 的序号（即位次）。

（1）首先，递归框架：

 /*
     递归划分结构框架
 */
 void split(int NodeNum,int order)
 {//NodeNum为当前子树结点数，order为当前子树在节点数为NodeNum时的序号
     if(NodeNum == ) //节点数为1 直接输出X 作为递归结束条件
    {cout<<"X";return;}
     else
     {
         if(LeftNum>)//左子树不为空
         {
             cout<<"(";
             split(,);
             cout<<")";
         }
         cout<<"X";//打印父节点X
         if(RightNum>)
         {
             cout<<"(";
             split(,);
             cout<<")";
         }
     }
 }

NodeNum=1为递归边界条件，表示这棵子树只有一个结点，打印该结点，并返回。

（2） 计算节点数为NodeNum，序号为order的树的左右子树有多少结点，即计算LeftNum和RightNum。

由题意可知，序号为1的左子树为空，右子树结点数为order，且为右斜树（所有的节点均在右子树上并且所有节点只有右孩子）；左右子树变换形态，此时左子树为空，右子树的形态数为catalan[order]；当右子树遍历完所有形态后，左子树节点数加一，右子树节点数减一，生成初始状态依然为右子树为右斜树，此时左子树有节点，也为右斜树（当然此时只有一个节点，即只有根节点）；左右子树变化形态，左子树形态数1，右子树形态数catalan[order-1]；左子树节点数+1，右子树节点数-1，依此类推。

　　当左子树有大于1个结点时，设为i个，左子树有catalan[i]种形态，左子树的每一种形态下，右子树节点数为NodeNum-i-1，形态数catalan[NodeNum-i-1]。

　　整个过程就像一个时钟计时一样，左子树是时针，右子树是分针，右子树全部变化完，左子树加1，但是与时钟不同的是：时钟是60进制的，二右子树是catalan[i]进制的，i会逐渐变为0。由此可以得出二叉树中左子树的节点数LeftNum: leftNum=min(i|catalan[0]*catalan[nodeNum-1]+catalan[1]*catalan[nodeNum-2]+...+catalan[i]*catalan[NodeNum-i-1]>=order)，右子树的节点数RightNum=NodeNum-LeftNum-1。

　　假设  所要求的树为  含有LeftNum个结点的左子树，RightNum个结点的右子树的二叉树是NodeNum个节点的二叉树  的第NewOrder棵树，则NewOrder=order-sum，其中sum=catalan(0)*catalan(NodeNum-1)+catalan(1)*catalan(NodeNum-2)+...+catalan(LeftNum-1)*catalan(RightNum+1)。

　　设左子树的应该是节点数为LeftNum的树的第LeftOrder个形态，右子树则应该是是节点数为RightNum的树的RightOrder个形态。其中LeftOrder=(NewOrder-1)/catalan(RightNum)+1，RightOrder=(NewOrder-1)%catalan(RightNum)+1。

　　此处应注意模数

 #include<iostream>
 using namespace std;
 long catalan[] = {,,,,,,,,,,,,,
           ,,,,,};
 void split(int NodeNum,int order)
 {
     if(NodeNum == ) {cout<<"X";return;}
     else
     {

         int sum=;
         int i;
         for(i=;sum<order;i++)
         {
             sum += catalan[i]*catalan[NodeNum-i-];
         }
         int LeftNum = --i;//左子树的节点个数
         int RightNum = NodeNum-LeftNum-;//右子树节点个数
         sum = sum - catalan[LeftNum]*catalan[RightNum];
         long NewOrder = order-sum;
         if(LeftNum>)
         {
             cout<<"(";
             split(LeftNum,(NewOrder-)/catalan[RightNum]+);
             cout<<")";
         }
         cout<<"X";
         if(RightNum>)
         {
             cout<<"(";
             split(RightNum,(NewOrder-)%catalan[RightNum]+);
             cout<<")";
         }
     }
 }
 int main()
 {
     long n;//n是序号

     while(cin>>n)
     {
         if(n == ) return ;//0为结束
         else
         {
             //首先得判断有几个结点
             int i,sum=;
             for(i=;sum<n;i++)//由于i=0不做任何操作，所以，从1开始
             {
                 sum+=catalan[i];
             }
             i--;sum = sum-catalan[i];
             //然后进行递归调用
             split(i,n-sum);//i个结点的第n-sum种情况
         }
         cout<<endl;

     }
     return ;
 }