8月清北学堂培训 Day 7

当天走得太兴奋了，忘记保存就关电脑了o(╥﹏╥)o，现在补上( p′︵‵。)

今天是杨思祺老师的讲授~

练习题

首先求出最短路；

如果选择的边不是最短路上的边，那么毫无影响；

对于最短路径上的边，我们需要枚举路径上每条边，加倍再跑 Dijkstra。

我们可以考虑在建图方面进行改造：

假设我们建完图之后是长这个样子的：

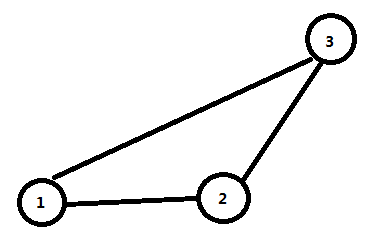
我们先考虑 k=1 的情况，也就是我们可以使一条边的权值变为0。

我们可以将这个图在上层拷贝一份，将每个结点从上层的能到达的结点连一条有向边，这些边的权值为0，这样就实现了删除一条边的效果：

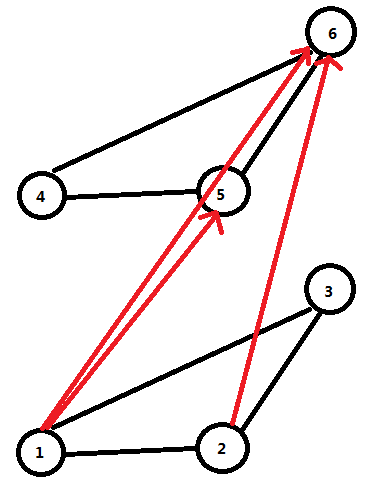
那么怎么设置上层点的编号呢？

我们可以像棋盘一样设置：

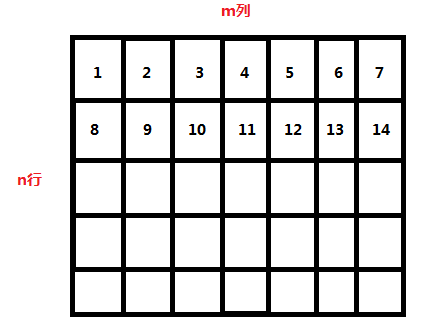
假设我们有个 n × m 的棋盘，那么这个棋盘上第 k 行第 j 列的数就是：（k-1）* m + j；

那么我们也可以根据这个规律来给上层的图的结点编号：（2-1）* n + j；

那么最终的答案就是：1 -> 6 的最短路，一遍Dijkstra 即可；

分析完上面 k=1 的情况后，我们就可以得出删除 k 条边的做法了：

我们拷贝 k 层图，按照上面的思路连权值为0的有向边，那么最后的答案就是：1 -> （k-1）*  n 点的最短路；

但是考虑到可能用不了 k 次更新（比如本来就不够 k 条边），所以我们再从分层图的每一层的点向下一层的对应点连一条边，表示白白浪费一次更新机会~

我们这样建边实现边的跳跃。

分层图的实现：通过映射，将二维图转化为一维图；

n² 建边，但是发现会有许多边是冗余的。

我们先按照 x 从小到大排好序；

假如平面内有三个点（x₁，y₁），（x₂，y₂），（x₃，y₃）；

第一个点到第三个点的直接路径为：min（| x₁- x₃ |，| y₁- y₃ |）= x₃ - x₁；

我们也可以考虑从中转点第二个点来走到第三个点：min（| x₁- x₂ |，| y₁- y₂ |）+ min（| x₂- x₃ |，| y₂- y₃ |）= x₂ - x₁ + x₃ - x₂ = x₃ - x₁；

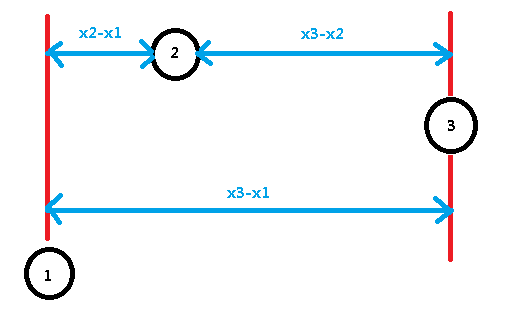
如果我们按照 x 排好序后，那么点 1 到点 3 的 x 距离完全可以用点 1 到点 2 + 点 2 到点 3 的 x 距离来表示；

也就是说，我们按照 x 排序后只需要在相邻两个点连一条边就好了；

对于 y 的话是一样的 。

我们尽量让最小边最大，但是这样操作会使最大边的选择范围变小，可能会导致最大边变大；

我们从大到小枚举最小边，用更大的边做 Kruskal，当 S 和 T 连通立即 break。

LCT，从大到小加边维护最小生成树。

1. 二分做法：

我们二分枚举 mid，小于 mid 的边连部落内部，大于等于 mid 的边是部落间的距离，看看是否连成了至少 k 个连通块即可 。

2. 最小生成树：

我们按照 Kruskal 的做法，当我们选中了 n-k 条边的时候，也就意味着此时有 k 个联通块，那么我们只需要再找一条不是部落间的边就是答案了，也就是选中的第 n-k+1 条边 。

我们需要求出每个杯子的奇偶性，才能知道答案，也就是要求每个 [ 0 , i ] 的奇偶性，就像前缀和一样，干脆直接用 S [ i ] 来表示区间 [ 0 , i ] 的奇偶性；

假如我们知道了区间 [ l , r ] 的奇偶性，那么我们就是知道了 S [ r ] - S [ l-1 ] 的奇偶性了；

奇偶性的转化：假如我们知道了 [ l , k ] 的奇偶性了，又知道了 [ k+1 , r ] 的奇偶性，那么我们也就知道了 [ l , r ] 的奇偶性！

我们发现这一点和树上唯一路径很像：知道了 x -> y 的路径，又知道了 y -> z 的路径，也就知道了 x -> z 的路径 。
那么通过这一条很重要的性质，我们求每个前缀和的话，其实就是求 0 都能走到每个点的最小花费和，再具体一点就是求最小代价使得整个图联通，直接最小生成树板子！

在任意一个非加油站点，不论目的地是哪个加油站，先前往最近 的加油站再前往目的地是最优策略。

加油站之间存在一种边，可以视为一条由非加油站点串起来的路径。我们希望找到加油站之间的最小生成树。

多源最短路，以所有加油站为起点，记录下每个点到最近加油站的距离，以及是哪个加油站。

建立用于做最小生成树之间的边：如果一条边 < u, v > 满足 u 和 v 的最近加油站不同，则 dis_u + dis_v + w_u,v 构成一条 from_u 和 from_v 的边。 MST 算法求出最小生成树，倍增或树链剖分维护链上最小值。

记四个关键点为 E₁,E₂,W₁,W₂。

一条边 < u, v, w > 在从 S 到 T 的最短路上，当且仅当 D_S,u + w + D_v,T D_u,v。 找出所有同时在 E₁ 到 E₂ 和 W₁ 到 W₂ 最短路上的有向边，一 定无环形成 DAG。 拓扑排序求 DAG 最长路。 注意：对于同时在 E₁ 到 E₂ 和 W₂ 到 W₁ 最短路上的有向边再做一次。

设 a [1] 是最小的，在模 a [1] 意义下，0 到 a [1] − 1 每个位置都 有其最小可被表示值。

而如果 k 是可被表示的，那么 k + a [1], k + 2 × a [1], . . . 都可被表示。

故问题转化为求解每个位置最小可被表示数字。 建立 a[1] 个点，对于每个 a [ j ]，j , 1，我们理解为可以花费 a [ j ] 代价从 x 点转移到 ( x + a [ j ] ) mod a [1] 点。建边之后从0 号点出发做单源最短路即可。