Fourier serie

你眼中看似落叶纷飞变化无常的世界，实际只是躺在上帝怀中一份早已谱好的乐章。

时域和频域就像观察一个物体一样，一个是主视图的，一个是侧视图。

1.在有限区间上由任意图形定义的任意函数都可以表示为单纯的正弦与余弦之和。

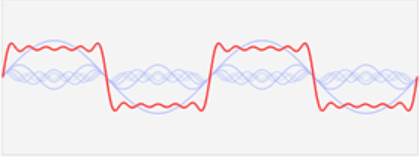
是由很多的正弦波叠加而成的。

不同与时域之中的函数变量是时间，频域中的变量是频率，所以时域中是按时间来排序的，频域中是按频率的大小来排序的。

而且频率中频率最低的那个波形的频率，规定它的频率为”1“。这样的话，为0的就代表直流成分，这只会抬高（或者降低）振幅。

频谱图的横坐标代表频率，纵坐标代表振幅。

为了弥补频谱图无法体现相位关系---相位谱。

相位谱：是由下往上看得到的，相当于一种仰视图的视角。

相位谱是选择一个基准，观测各个频谱分量最近的最低点到基准的距离，而单位正好是时间（差）。

PS：时间差和相位差是不一样的，两者之间需要一定的转换。