NFA 确定化为 DFA

子集法：

f(q,a)={q1,q2,…,qn},状态集的子集

将{q1,q2,…,qn}看做一个状态A，去记录NFA读入输入符号之后可能达到的所有状态的集合。

步骤：

1.根据NFA构造DFA状态转换矩阵

①确定DFA初态（NFA的所有初态集），字母表

②从初态出发，经字母表到达的状态集看成一个新状态

③将新状态添加到DFA状态集

④重复23步骤，直到没有新的DFA状态

2.画出DFA

3.看NFA和DFA识别的符号串是否一致。

练习：

1.解决多值映射：子集法

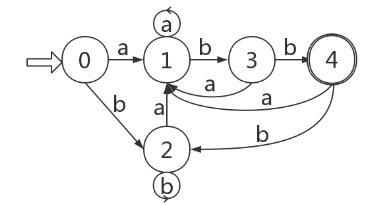
1）. 发给大家的图1

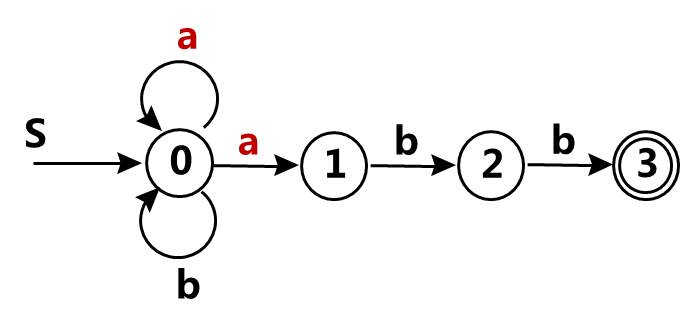
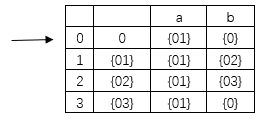
2）. P64页练习3

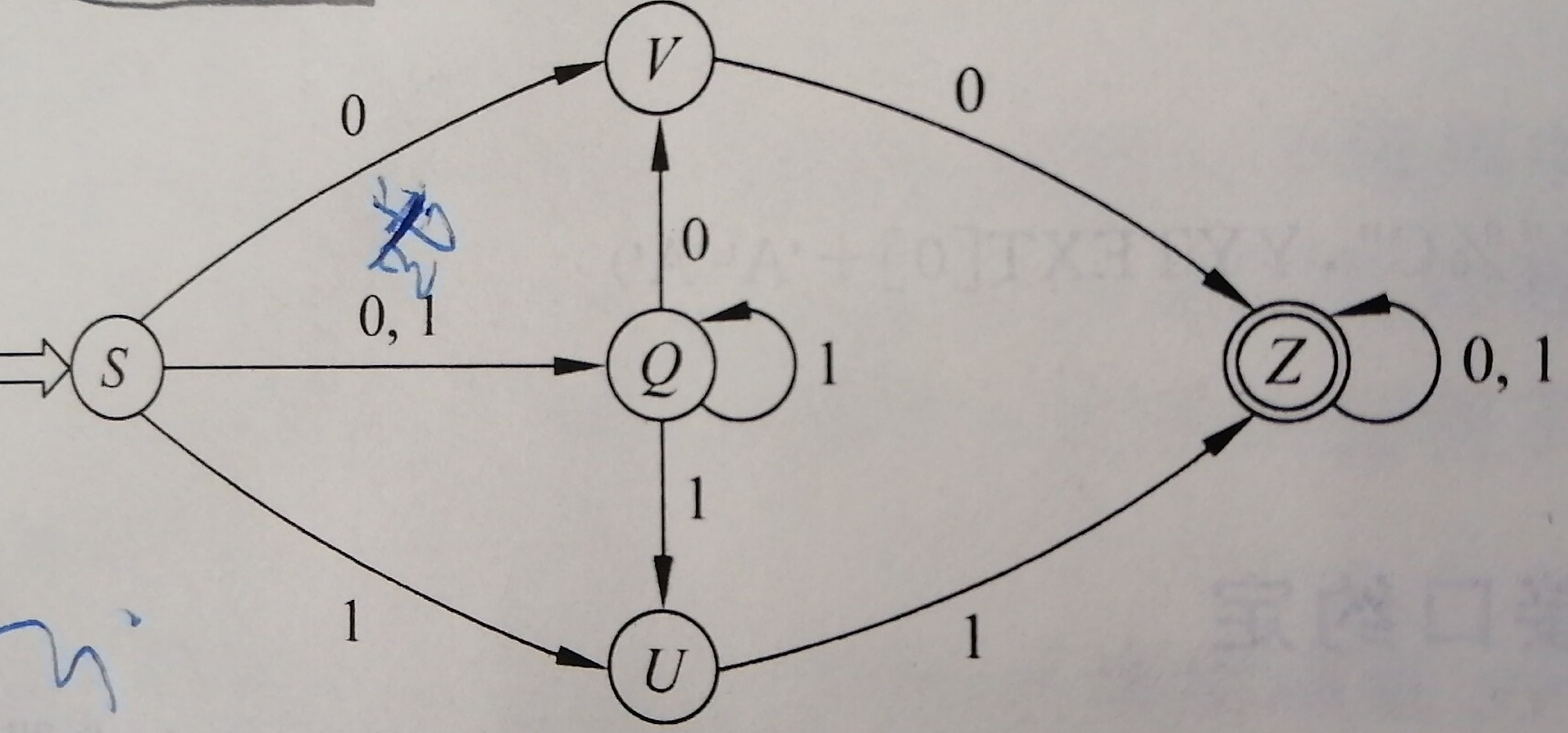
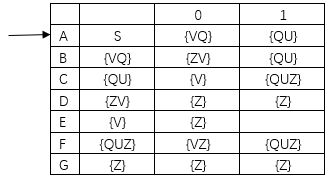
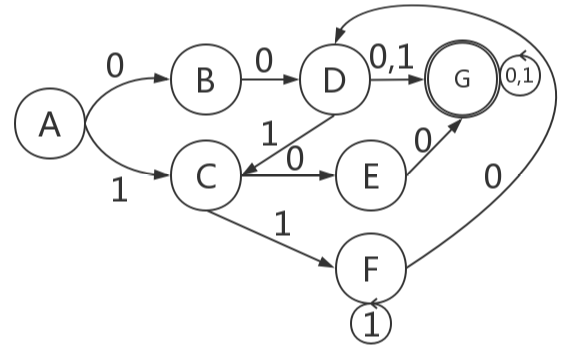
2.解决空弧：对初态和所有新状态求ε－闭包

1）. 发给大家的图2

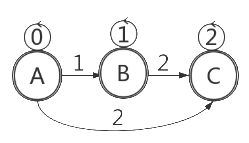
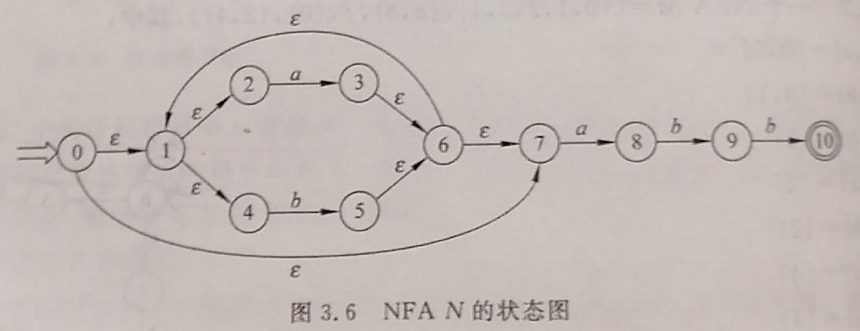
2）.P50图3.6

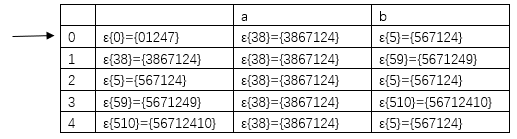
作业八——非确定的自动机NFA确定化为DFA的更多相关文章

  1. 第八次作业-非确定的自动机NFA确定化为DFA

    NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. 步骤: 1. ...

  2. 第八次-非确定的自动机NFA确定化为DFA

     提交作业 NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. ...

  3. 第八次——非确定的自动机NFA确定化为DFA

    NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. 步骤: 1. ...

  4. 非确定的自动机NFA确定化为DFA

    摘要: 在编译系统中,词法分析阶段是整个编译系统的基础.对于单词的识别,有限自动机FA是一种十分有效的工具.有限自动机由其映射f是否为单值而分为确定的有限自动机DFA和非确定的有限自动机NFA.在非确 ...

  5. 编译原理之非确定的自动机NFA确定化为DFA

    1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} ),其中 f(0,a)={0,1}  f(0,b)={0}  f(1,b)={2}  f(2,b)={3} 画出状态转换矩阵 ...

  6. 编译原理：非确定的自动机NFA确定化为DFA

    1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} ),其中 f(0,a)={0,1}  f(0,b)={0}  f(1,b)={2}  f(2,b)={3} 画出状态转换矩阵 ...

  7. NFA转化为DFA

    NFA(不确定的有穷自动机)转化为DFA(确定的有穷自动机) NFA转换DFA,通常是将带空串的NFA(即:ε-NFA)先转化为不带空串的NFA(即:NFA),然后再转化为DFA. 提示:ε是空串的意 ...

  8. 非确定有限状态自动机的构建（二）——将CharVal转换为NFA

    保留版权,转载注明出处:潘军彪的个人博客(http://blog.csdn.net/panjunbiao/article/details/9378933) 将上下文无关文法读入内存之后,可以将它转换成 ...

  9. 非确定有限状态自动机的构建（一）——NFA的定义和实现

    保留版权,转载需注明出处(http://blog.csdn.net/panjunbiao). 非确定有限状态自动机(Nondeterministic Finite Automata,NFA)由以下元素 ...

随机推荐

  1. 【SQL】在数据库中发起http请求的小改进

    市面上常见的是用MSXML2.ServerXMLHTTP这个类,但这个类在发起异步请求时并不可靠,就是当send后并不一定会发出这个请求.这里推荐改用Microsoft.XMLHTTP,如果只是简单的 ...

  2. ES6、ES7、ES8、ES9、ES10

    ES6新特性(2015) ES6的特性比较多,在 ES5 发布近 6 年(2009-11 至 2015-6)之后才将其标准化.两个发布版本之间时间跨度很大,所以ES6中的特性比较多.在这里列举几个常用 ...

  3. PJzhang:docker基础知识的2个疗程-one

    猫宁!!! 参考:http://virtual.51cto.com/art/201805/572135.htm https://www.cnblogs.com/rkit/p/9237696.html ...

  4. Awvs–网络漏洞扫描工具

    Awvs漏洞扫描自动化 在WEB安全方面,安全侧使用Acunetix_Web_Vulnerability_Scanner_11.xWEB漏洞扫描工具定期手工对m站和www站进行全站漏洞扫描. 为了防止 ...

  5. Webpack实现按需打包Lodash的几种方法详解

    参考链接:https://www.jb51.net/article/113235.htm 在vue-cli3中需要将babel-preset-es2015插件更换为@babel/preset-env插 ...

  6. elasticsearch安装ik

    https://github.com/medcl/elasticsearch-analysis-ik/releases下载对应的ik plugins/目录下创建analysis-ik,再将上述中的zi ...

  7. 什么是大数据计算服务MaxCompute

    大数据计算服务(MaxCompute,原名ODPS)是一种快速.完全托管的EB级数据仓库解决方案. 当今社会数据收集手段不断丰富,行业数据大量积累,数据规模已增长到了传统软件行业无法承载的海量数据(百 ...

  8. WinForm打包

    首先要在想要打包的项目下创建一个新的项目, 创建好setup项目,之后点击属性,去修改打包软件的名字,ProductName....可以选填 到此已经创建好了setup工程了,那么下面开始将要打包的d ...

  9. hdu 1029 求出现次数过半的数

    题目传送门//res tp hdu 已知必定存在一个元素出现次数超过一半,考虑用栈 若当前元素等于栈顶元素,入栈,反之出栈,并将当前元素入栈 最终的栈顶元素即是所求 #include<iostr ...

  10. linux 从远程服务器拷贝文件

    1.从服务器复制文件到本地: scp root@192.168.1.100:/data/test.txt /home/myfile/ 2.从服务器复制文件夹到本地: scp -r root@192.1 ...