[Scikit-learn] 1.1 Generalized Linear Models

1.1.10. Bayesian Ridge Regression

首先了解一些背景知识：from: https://www.r-bloggers.com/the-bayesian-approach-to-ridge-regression/

In this post, we are going to be taking a computational approach to demonstrating the equivalence of the bayesian approach and ridge regression.

From: 文本语言模型的参数估计-最大似然估计、MAP及贝叶斯估计

三类参数估计方法：最大似然估计MLE、最大后验概率估计MAP、贝叶斯估计。

最大似然估计MLE

关键：写出似然函数

最大后验概率估计MAP

最大后验估计与最大似然估计相似，不同点在于估计 $\theta$ 的函数中允许加入一个先验 $p(\theta)$ ，也就是说此时不是要求似然函数最大，而是要求由贝叶斯公式计算出的整个后验概率最大，即

$\begin{aligned} \hat{\theta}_{MAP} &= argmax_\theta \frac{p(X | \theta) p(\theta)}{p(X)}\\ &= argmax_\theta p(X | \theta)p(\theta) \\ &= argmax_\theta \{L(\theta|X) + \log p(\theta)\}\\ &= argmax_\theta \{\sum_{x \in X} \log p(x | \theta) + \log p(\theta)\} \end{aligned}$

注意这里P（X）与参数 $\theta$ 无关，因此等价于要使分子最大。与最大似然估计相比，现在需要多加上一个先验分布概率的对数。

【在样本足够大时，结果逼近MLE】

【加了先验没什么神秘的，效果很类似l正则项】

贝叶斯估计

贝叶斯估计是在MAP上做进一步拓展，此时不直接估计参数的值，而是允许参数服从一定概率分布。回顾一下贝叶斯公式

$p(\theta|X) = \frac{p(X|\theta) \cdot p(\theta)}{p(X)}$

现在不是要求后验概率最大，这样就需要求 $p(X)$ ，即观察到的evidence的概率，由全概率公式展开可得

$p(X) = \int_{\theta \in \Theta}p(X|\theta)p(\theta)d\theta$

当新的数据被观察到时，后验概率可以自动随之调整。但是通常这个全概率的求法是贝叶斯估计比较有技巧性的地方。

那么如何用贝叶斯估计来做预测呢？如果我们想求一个新值 $\hat{x}$ 的概率，可以由

$p(\hat{x}|X) = \int_{\theta \in \Theta} p(\hat{x} | \theta)p(\theta|X)d\theta=\int_{\theta \in \Theta}p(\hat{x}|\theta)\frac{p(X|\theta)p(\theta)}{p(X)}d\theta$

来计算。注意此时第二项因子在 $\theta \in \Theta$ 上的积分不再等于1，这就是和MLE及MAP很大的不同点。

我们仍然以扔硬币的伯努利实验为例来说明。和MAP中一样，我们假设先验分布为Beta分布，

但是构造贝叶斯估计时，

- 不是要求用后验最大时的参数来近似作为参数值，
- 而是求满足Beta分布的参数p的期望，有

注意这里用到了公式

$\int_p\prod_{t=1}^{|T|}P_t^{\alpha_t - 1} = B(\alpha)$

当T为二维的情形可以对Beta分布来应用；T为多维的情形可以对狄利克雷分布应用

根据结果可以知道，根据贝叶斯估计，参数p服从一个新的Beta分布。回忆一下，我们为p选取的先验分布是Beta分布，然后以p为参数的二项分布用贝叶斯估计得到的后验概率仍然服从Beta分布，由此我们说二项分布和Beta分布是共轭分布。在概率语言模型中，通常选取共轭分布作为先验，可以带来计算上的方便性。最典型的就是LDA中每个文档中词的Topic分布服从Multinomial分布，其先验选取共轭分布即Dirichlet分布；每个Topic下词的分布服从Multinomial分布，其先验也同样选取共轭分布即Dirichlet分布。

根据Beta分布的期望和方差计算公式，我们有

可以看出此时估计的p的期望和MLE ，MAP中得到的估计值都不同，此时如果仍然是做20次实验，12次正面，8次反面，那么我们根据贝叶斯估计得到的p满足参数为12+5和8+5的Beta分布，其均值和方差分别是17/30=0.567, 17*13/(31*30^2)=0.0079。可以看到此时求出的p的期望比MLE和MAP得到的估计值都小，更加接近0.5。

结论：

综上所述我们可以可视化MLE,MAP和贝叶斯估计对参数的估计结果如下

个人理解是，从MLE到MAP再到贝叶斯估计，对参数的表示越来越精确【应该是表达越来越丰富，毕竟由一个值变为了一个分布，减少了推断过程中信息的损失】，得到的参数估计结果也越来越接近0.5这个先验概率，越来越能够反映基于样本的真实参数情况。【一般都用贝叶斯估计】

链接：https://www.zhihu.com/question/22007264/answer/20014371

过去的线性归回，比如使用最小二乘，其实就是相当于最大似然的感觉，容易overfitting。

采用了贝叶斯，假设了高斯分布，也就等价于Ridge Regression。

如果假设是拉普拉斯分布，就等价于LASSO。

Train:

>>> from sklearn import linear_model

>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]

>>> Y = [0., 1., 2., 3.]

>>> reg = linear_model.BayesianRidge()

>>> reg.fit(X, Y)

BayesianRidge(alpha_1=1e-06, alpha_2=1e-06, compute_score=False, copy_X=True,

       fit_intercept=True, lambda_1=1e-06, lambda_2=1e-06, n_iter=300,

       normalize=False, tol=0.001, verbose=False)

Predict:

>>> reg.predict ([[1, 0.]])

array([ 0.50000013])

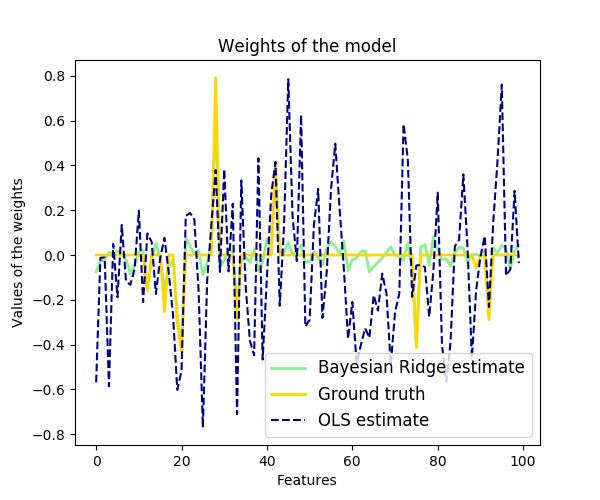
Demo: