算法：二叉树的层次遍历（递归实现+非递归实现，lua）

二叉树知识参考：深入学习二叉树(一) 二叉树基础

递归实现层次遍历算法参考：【面经】用递归方法对二叉树进行层次遍历 && 二叉树深度

上面第一篇基础写得不错，不了解二叉树的值得一看。

用递归来实现二叉树的层次遍历。lua实现

先上代码：

function FindTree(tree, callback)
   local function Find(tree, level)
       if(tree == nil or level <= ) then
         return false;
       end
       if (level == ) then
         if callback then
            callback(tree.data);
         end
         return true;
       end

       local has_left = Find(tree.left, level - );
       local has_right = Find(tree.right, level - );

       return has_left or has_right;
   end

   local level = ;
   while Find(tree, level, callback) do
       level = level + ;
   end
end

测试代码：

a={};
a.data = "a"

b, c = {}, {}
b.data = "b"
c.data = "c"
a.left = b
a.right = c

d, e, f, g = {}, {}, {}, {}
d.data = "d"
e.data = "e"
f.data = "f"
g.data = "g"
b.left = d
b.right = e
c.left = f
c.right = g

h, i, j = {}, {}, {}
h.data = "h"
i.data = "i"
j.data = "j"
d.left = h
d.right = i
e.left = j

local  list = {}
FindTree(a, function(data)
   table.insert(list, data)
end)

print(table.concat(list, ", "))

结果：

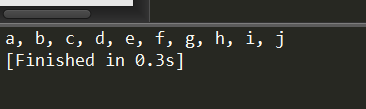
基本思路 （下面的a是测试树的根结点）：

每步，都是一次从根到当前层级的自上而下的一次遍历，从上到下找到第1层a,  从上到下找到第2层b,c，从上到下找到第3层d,e,f,g

详细步骤：

1，FindTree(a, 1) : 如果此树深度大于等于1，a结点的data通过回调传回，函数返回true , while循环继续；如果深度为0，a==null，直接返回false，while循环结束。

2，FindTree(a, 2)：如果此树深度大于等于2，传回a的子结点（上图b位置，或c位置，或bc位置）的data，返回true , while循环继续；如果深度小于2，返回false，while循环结束。

　　这里就比较复杂了，需要对函数递归有一定的了解。执行到 has_left = FindTree(tree.left, level - 1); 时，现场被保留（后续代码暂时不执行），程序再次进入到FindTree函数（即执行has_left = FindTree(b, 1)），当a有左子节点时，传回a的左子节点的data，返回true，即 has_left =true; 否则 has_left = false;  然后执行到has_right = FindTree(tree.right, level - 1); 同理，如果有右子节点，传回a的右子节点的data，返回true，即 has_right=true; 否则 has_right= false。如果a有左子节点或右子节点（或都有），整个函数返回true，while循环继续；如果a没有左结点和右结点，即深度小于2，has_left or has_right = false ，while循环结束。

3，FindTree(a, 3)：如果此树深度大于等于3，传回a的深度为3的子结点（上图d, e, f, g的各位置随意组合）的data，返回true , while循环继续；如果深度小于2，返回false，while循环结束。

　　同理，执行到 has_left = FindTree(tree.left, level - 1); 时，现场保留，直到has_left = FindTree(tree.left.left, level - 1 - 1); 即has_left = FindTree(d, 1)，如果d结点不存在，返回false，has_left = false; 如果存在，打印d结点的data，返回true，has_left = true; e, f, g各个位置 的检测同理。

4，…… ， n - 1,

n，FindTree(a, n): 深度小于n (此树深度为n-1)，返回false，while循环结束。

用非递归来实现二叉树的层次遍历。lua实现

先上代码：

function FindTree2(tree, callback)
   local  nodeList = {tree}
   while #nodeList >  do
      local  tempList = {}
      for i, v in ipairs(nodeList) do
         if callback then
            callback(v.data)
         end
         table.insert(tempList, v.left)
         table.insert(tempList, v.right)
      end
      nodeList = tempList;
   end
end

测试代码：如上

测试如果：如上

基本思路：从上到下，每一层从左到右依次遍历。把每一层子节点存放在一个列表，直到这个列表为空，则遍历完成。

这个方式比较直观，直接看一下上面的图和代码，很容易理解。