移动端H5地图矢量SHP网格切分打包方案

文章版权由作者李晓晖和博客园共有，若转载请于明显处标明出处：http://www.cnblogs.com/naaoveGIS/

1.背景

与离线瓦片方案一样，同样是为了解决移动端网速和流量问题，但是却不仅仅于此。传统的矢量数据的展示一般分为两种方案：

• 通过WMS动态获取范围内的矢量数据图片（矢量数据由后台处理成一张图片返回），在前端叠加展示。
  优点——渲染压力在后端，前端无压力。后台对图片更容易做缓存（前端把地图切分成格网，以WMS请求模拟WMTS请求）。
  缺点——当前端需要交互时，必须进行动态的根据坐标查询地理服务器（I查询）。响应稍慢，对后端压力大。
• 通过WFS服务获取范围内的矢量数据文本（geojson、pbf等格式），前端解析返回数据动态渲染。
  优点——由于是前端渲染展示，交互便捷，并且可以在前段只有控制样式。
  缺点——后台和前端在获取数据和展示数据上均有压力，当数据量特别大时，前端渲染耗费性能容易卡顿。

而该方案上，当我们将SHP矢量数据以一定算法处理成文本文件存放到移动端后，既可以避免动态获取数据对服务端的压力，也可以拥有WFS方案上在前端实时渲染数据时的样式制定和交互便捷的优点。
整个方案优点总结为：

• 规避手机网速问题
• 规避手机流量问题
• 减少服务端压力
• 前端要素展示样式可定制
• 要素交互快速响应

2.两种离线算法，两种离线矢量数据处理方案的描述对比

2.1方案一（分级矢量切片方案）

方案描述

矢量切片方案在我之前的文章中均有描述：项目角度谈矢量切片运用以及Geoserver处理自定义规格矢量切片方案以及WebGIS中矢量切图的初步研究。简单叙述为：

• 把矢量数据当做瓦片处理，根据切图原点、瓦片大小、各级别分辨率，先在不同级别对SHP进行抽稀简化，然后将该级别的SHP切分成对应矢量数据块，再处理成文本格式。
• 将矢量切片上传至移动端，H5地图请求获取本地矢量切片，解析渲染。

方案分析

• 优点: 各级别数据抽稀切片，使得各级别数据量加载均可控制，前端渲染数量也处于可控状态。
• 缺点：由于要切不同级别下的数据，矢量切片比较耗费时间，而且切图数据量大。不利于快速实施。

2.2方案二（固定网格切片方案）

方案描述

• 以固定几何大小的网格对SHP数据切片处理成文本。
• 前端实时根据此时的可视范围，基于预制的网格切片大小，算出此时范围下对应的各切片，请求加载，解析渲染。

方案分析

• 优点：只需根据预制的网格大小将矢量数据一次切割生成，效率比较高。
• 缺点：在地图级别很小显示全图时，加载的切片数量过多导致前端渲染压力非常大。

2.3方案选型

• 方案二优于方案一最大的地方在于实施更快速。
• 方案二最大的缺点是在低地图级别时显示的数据过量问题，这里可以通过两个手段规避。
  控制显示层级——即只让地图缩放至某个级别上时才加载该矢量数据。
  控制显示数量——将网格数据进一步以责任网格打包，固定人员只展示固定责任网格范围内的数据。

3.矢量数据网格切分打包工具的实现

3.1SHP数据网格切分详细描述

• 获得该图层的几何范围，依据切图原点、网格大小，算出该图层对应的网格数量（colnums、rownums）以及网格的起始切片的行列编号(startcolnum、startrownum）。
• 以colnums和rownums作为双循环遍历结束点，依次将图层中的要素切片，处理成文本文件。
  代码描述：

//计算格网行列号
int colNums = 0, rowNums = 0;
colNums = Convert.ToInt32(Math.Ceiling((_maxX - _minX) / inputGridSize));
rowNums = Convert.ToInt32(Math.Ceiling((_maxY - _minY) / inputGridSize));

3.2基于单元网格的已有切片打包描述

选用单元网格图层进行打包，主要原因为单元网格为最小划分网格，变动相对较少，减少实施次数。利用网格将已有的切片再进行整合打包，可进一步控制前端展示时的矢量数据数量。

• 遍历获取网格图层中的网格要素，得到各要素的几何范围。
• 依据几何范围、网格大小、切图原点，算出该范围内包含的瓦片编号。
• 将这些瓦片拷贝至以（要素编码\部件类型编号)命名的文件夹中。
• 遍历处理完所有数据拷贝后，进行整体的文件压缩。

注意：
瓦片的打包路径规范为：

工具界面为: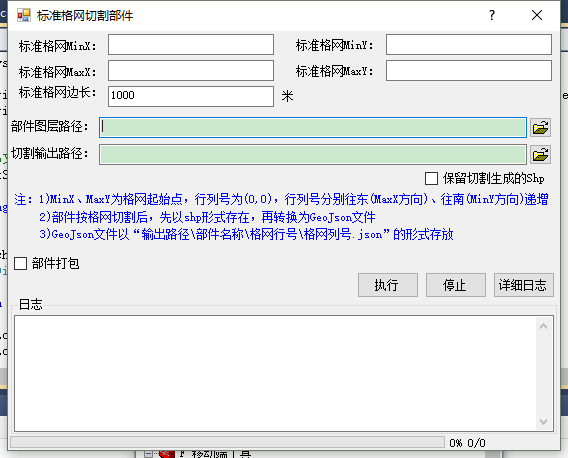

4.H5地图前端展示实现

4.1详细描述

前端展示所用算法与网格打包时所用算法相同。JS获取本地数据的思想方法也与我在移动端H5地图离线瓦片方案中描述的移动端读取本地瓦片的方法相同。不做累述，核心代码如下:

var originx=parseFloat(gridClipParams[0]);
var originy=parseFloat(gridClipParams[1]);
var size=parseFloat(gridClipParams[2]);
var vectorSource = new VectorSource({
	format:format,
	url:function(extent) {
		var temurl=GeosService.queryContent(url,servicelayerid,where,extent);
		if(useMobileCache){
			var col=Math.floor(Math.abs((extent[0]-originx))/size);
			var row=Math.floor(Math.abs((extent[1]-originy))/size);
			//本地测试url
			//temurl="http://192.168.32.135:8080/gis/tilemap/11010100100907/"+subtypeid+"/"+row+"/"+col+".json";
			temurl =self.offlineURL+encodeURIComponent(temurl)+"&row="+row+"&col="+ col+"&layername="+subtypeid;
		}
		return temurl;
	},
	strategy: function(extent,resolution){
		var minx=extent[0]-size;
		var miny=extent[1]-size;
		var maxx=extent[2]+size;
		var maxy=extent[3]+size;
		var m=Math.ceil((maxx-minx)/size);
		var n=Math.ceil((maxy-miny)/size);
		var extentArr=new Array();
		for(var i=0;i<m;i++){
			for(var j=0;j<n;j++){
				var temextent=[];
				var temminx=minx+i*size;
				var temminy=miny+j*size;
				var temmaxx=minx+(i+1)*size;
				var temmaxy=miny+(j+1)*size;
				temextent=[temminx,temminy,temmaxx,temmaxy];
				extentArr.push(temextent);
			}
		}
		return extentArr;
	}
});

4.2成果展示

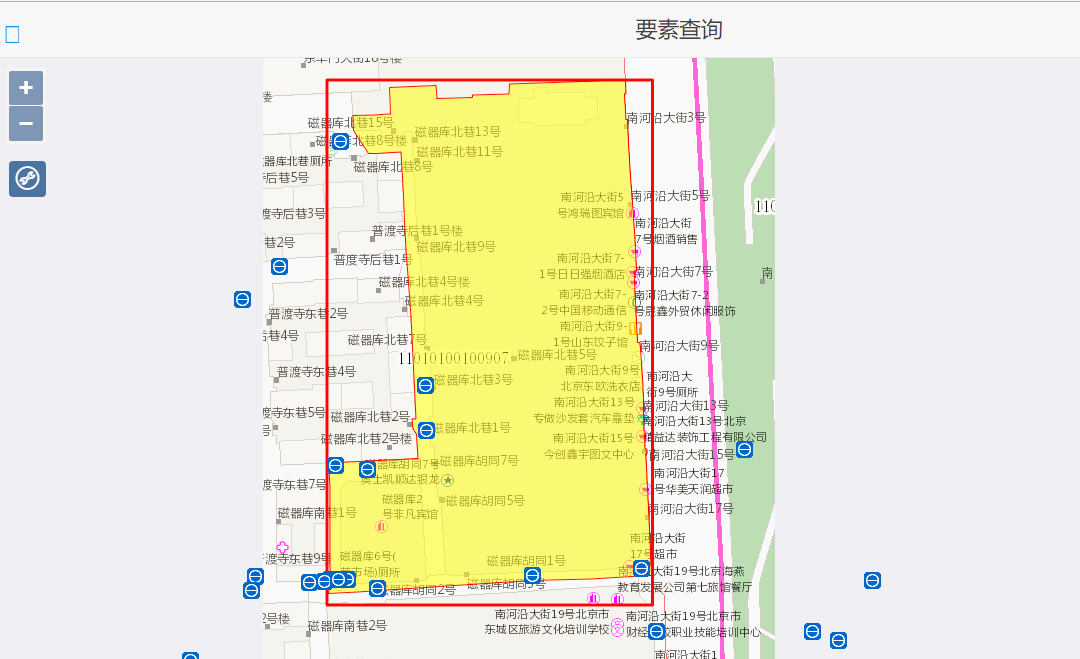
由于部件打包是以1000米的网格进行划分后再打包，可以看见有的不在单元网格区划内的部件也展示在了地图上。所以网格切分的大小是一个必须根据项目进行调整的参数。

5.移动端打包上传详细描述

我将打包上传单独进行描述，是因为这一块整合时需要格外注意文件的合并方式。

• 手机服务端获取到责任网格与单元网格的对应关系。
• 将责任网格对应的所有单元网格下的文件进行合并。合并规则为增盖方式。合并后的文件夹名称为责任网格命名。

责任网格打包文件夹的路径说明: \责任网格编码\部件小类\行号\列号.json

　　　　　　　　　　　　　　　　　　　　　  　-----欢迎转载，但保留版权，请于明显处标明出处：http://www.cnblogs.com/naaoveGIS/

　　    如果您觉得本文确实帮助了您，可以微信扫一扫，进行小额的打赏和鼓励，谢谢 ^_^