选择排序—堆排序（Heap Sort） 没看明白，不解释

堆排序是一种树形选择排序，是对直接选择排序的有效改进。

基本思想：

堆的定义如下：具有n个元素的序列（k1,k2,...,kn),当且仅当满足

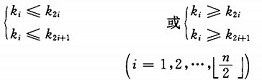
时称之为堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最小项（小顶堆）。
若以一维数组存储一个堆，则堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的。如：

（a）大顶堆序列：（96, 83,27,38,11,09)

(b)  小顶堆序列：（12，36，24，85，47，30，53，91）

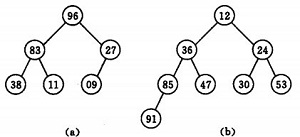
初始时把要排序的n个数的序列看作是一棵顺序存储的二叉树（一维数组存储二叉树），调整它们的存储序，使之成为一个堆，将堆顶元素输出，得到n 个元素中最小(或最大)的元素，这时堆的根节点的数最小（或者最大）。然后对前面(n-1)个元素重新调整使之成为堆，输出堆顶元素，得到n 个元素中次小(或次大)的元素。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。称这个过程为堆排序。

因此，实现堆排序需解决两个问题：
1. 如何将n 个待排序的数建成堆；
2. 输出堆顶元素后，怎样调整剩余n-1 个元素，使其成为一个新堆。

首先讨论第二个问题：输出堆顶元素后，对剩余n-1元素重新建成堆的调整过程。
调整小顶堆的方法：

1）设有m 个元素的堆，输出堆顶元素后，剩下m-1 个元素。将堆底元素送入堆顶（（最后一个元素与堆顶进行交换），堆被破坏，其原因仅是根结点不满足堆的性质。

2）将根结点与左、右子树中较小元素的进行交换。

3）若与左子树交换：如果左子树堆被破坏，即左子树的根结点不满足堆的性质，则重复方法 （2）.

4）若与右子树交换，如果右子树堆被破坏，即右子树的根结点不满足堆的性质。则重复方法 （2）.

5）继续对不满足堆性质的子树进行上述交换操作，直到叶子结点，堆被建成。

称这个自根结点到叶子结点的调整过程为筛选。如图：

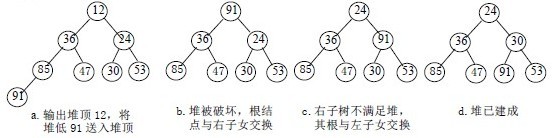
再讨论对n 个元素初始建堆的过程。
建堆方法：对初始序列建堆的过程，就是一个反复进行筛选的过程。

1）n 个结点的完全二叉树，则最后一个结点是第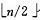个结点的子树。

2）筛选从第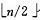个结点为根的子树开始，该子树成为堆。

3）之后向前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点。

如图建堆初始过程：无序序列：（49，38，65，97，76，13，27，49）
                             

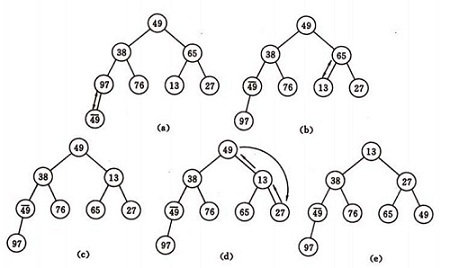
 算法的实现：

从算法描述来看，堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数，二是反复调用渗透函数实现排序的函数。

void print(int a[], int n){
	for(int j= 0; j<n; j++){
		cout<<a[j] <<"  ";
	}
	cout<<endl;
}

/**
 * 已知H[s…m]除了H[s] 外均满足堆的定义
 * 调整H[s],使其成为大顶堆.即将对第s个结点为根的子树筛选,
 *
 * @param H是待调整的堆数组
 * @param s是待调整的数组元素的位置
 * @param length是数组的长度
 *
 */
void HeapAdjust(int H[],int s, int length)
{
	int tmp  = H[s];
	int child = 2*s+1; //左孩子结点的位置。(i+1 为当前调整结点的右孩子结点的位置)
    while (child < length) {
		if(child+1 <length && H[child]<H[child+1]) { // 如果右孩子大于左孩子(找到比当前待调整结点大的孩子结点)
			++child ;
		}
		if(H[s]<H[child]) {  // 如果较大的子结点大于父结点
			H[s] = H[child]; // 那么把较大的子结点往上移动，替换它的父结点
			s = child;		 // 重新设置s ,即待调整的下一个结点的位置
			child = 2*s+1;
		}  else {			 // 如果当前待调整结点大于它的左右孩子，则不需要调整，直接退出
			 break;
		}
		H[s] = tmp;			// 当前待调整的结点放到比其大的孩子结点位置上
	}
	print(H,length);
}

/**
 * 初始堆进行调整
 * 将H[0..length-1]建成堆
 * 调整完之后第一个元素是序列的最小的元素
 */
void BuildingHeap(int H[], int length)
{
	//最后一个有孩子的节点的位置 i=  (length -1) / 2
	for (int i = (length -1) / 2 ; i >= 0; --i)
		HeapAdjust(H,i,length);
}
/**
 * 堆排序算法
 */
void HeapSort(int H[],int length)
{
    //初始堆
	BuildingHeap(H, length);
	//从最后一个元素开始对序列进行调整
	for (int i = length - 1; i > 0; --i)
	{
		//交换堆顶元素H[0]和堆中最后一个元素
		int temp = H[i]; H[i] = H[0]; H[0] = temp;
		//每次交换堆顶元素和堆中最后一个元素之后，都要对堆进行调整
		HeapAdjust(H,0,i);
  }
} 

int main(){
	int H[10] = {3,1,5,7,2,4,9,6,10,8};
	cout<<"初始值：";
	print(H,10);
	HeapSort(H,10);
	//selectSort(a, 8);
	cout<<"结果：";
	print(H,10);

}

分析:

设树深度为k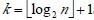，。从根到叶的筛选，元素比较次数至多2(k-1)次，交换记录至多k 次。所以，在建好堆后，排序过程中的筛选次数不超过下式：

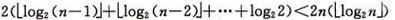
而建堆时的比较次数不超过4n 次，因此堆排序最坏情况下，时间复杂度也为：O(nlogn )。