Gradient Descent

理自Andrew Ng的machine learning课程。

目录：

• 梯度下降算法
• 梯度下降算法的直观展示
• 线性回归中的梯度下降

前提：

线性回归模型 ：$h(\theta_0,\theta_1)=\theta_0+\theta_1x$

损失函数：$J(\theta_0,\theta_1)=\frac{1}{2m} \sum_{i=1}^m (h_\theta(x^(i))-y^(i))^2$

1、梯度下降算法

目的：求解出模型的参数 / estimate the parameters in the hypothesis function

如下图所示，$\theta_0,\theta_1$代表模型的参数，$J(\theta_0,\theta_1)$代表模型的损失函数

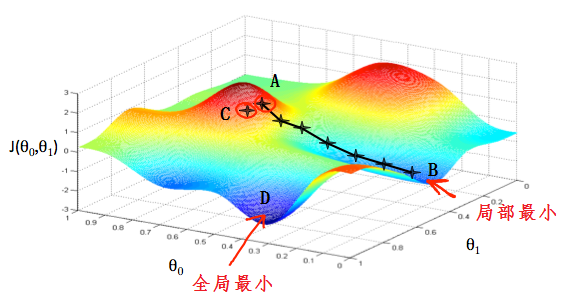
目的：从某一点出发，走到最低点。

怎么走：沿着所在点处最陡的方向下降。某一点山坡最陡的方向就是这一点的切线方向，也就是这一点的导数。每一步走多大取决于学习率$\alpha$。

在图中，每一个十字星之间的距离取决与$\alpha$的大小。小的$\alpha$会使两点之间的距离比较小，大的$\alpha$会产生大的步距。每一步走的方向取决于所在点的偏导。不同的起始点会有不同的终点，如上图从A出发最终到达B，而从C出发最终到达D。

梯度下降算法如下：

$\theta_j:=\theta_j-\alpha\frac{\partial}{\partial \theta_j}J(\theta_0,\theta_1)$    repeat util convergence

注意：$\theta_0,\theta_1$在每一步的迭代中都是同步更新的

2、梯度下降算法的直观展示

如下图：此图是一个损失函数的图像

当$\theta_1$在最小值点的右边时，图像的斜率（导数）是正的，学习率$\alpha$也是正的，根据梯度下降算法的公式，更新后的$\theta_1$是往左边方向走了，的确是朝着最小值点去了；

当$\theta_1$在最小值点的左边时，图像的斜率（导数）是负的，学习率$\alpha$是正的，根据梯度下降算法的公式，更新后的$\theta_1$是往右边方向走了，也是朝着最小值点去了；

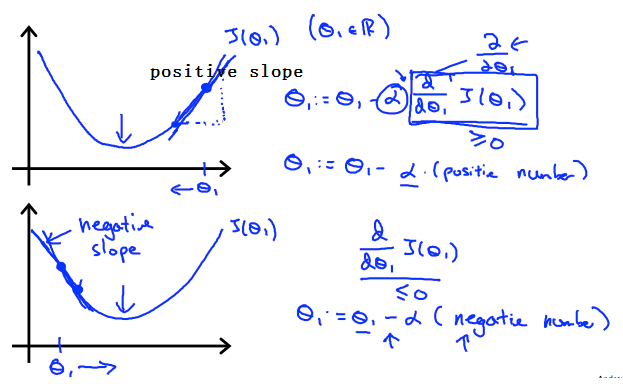
另外，我们需要调整$\alpha$使的算法可以在一定的时间内收敛。收敛失败或者收敛的非常慢，都说明使用的步长$\alpha$是错误的。

如果使用固定的$\alpha$，算法会收敛吗？

梯度下降算法隐含的一个信息就是，当点越来越接近最小值点的时候，梯度也会越来越小，到达最小值点时，梯度为0；

所以即使不去调整$\alpha$，走的步长也是会越来越短的，算法最终也还是会收敛的，所以没必要每次都调整$\alpha$的大小。

3、线性回归中的梯度下降算法

当把梯度下降算法具体的运用到线性回归上去的时候，算法就可以在偏导部分写的更加具体了：

repear until convergence {

$\qquad \theta_0:=\theta_0-\alpha \frac {1}{m} \sum_{i=1}^m (h_\theta(x_i)-y_i)$

$\qquad \theta_1:=\theta_1-\alpha \frac {1}{m} \sum_{i=1}^m ((h_\theta(x_i)-y_i)x_i)$

}

batch gradient descent

以上：在每一步更新参数时，让所有的训练样本都参与更新的做法，称为batch gradient descent；

注意到：虽然梯度下降算法可能会陷入局部最优的情况，但是在线性回归中不存在这种问题，线性回归只有一个全局最优，没有局部最优，算法最终一定可以找到全局最优点（假设$\alpha$不是特别大）。

线性回归中，J是一个凸二次函数，这样的函数是碗状的（bowl-shaped），没有局部最优，只有一个全局最优。