常见的概率分布类型（Probability Distribution）

统计学中最常见的几种概率分布分别是正态分布（normal distribution），t分布（t distribution），F分布（F distribution）和卡方分布（χ2 distribution，chi-square distribution），其中后三种属于抽样分布。

为什么要研究概率分布呢？因为通过研究概率分布，我们可以找出数据的分布规律，并根据这些规律来解决特定条件下的问题。比如：假设随机变量X服从某个已知的分布，我们就可以利用这个分布对X的取值是否显著异于分布期望值进行检验。

下面来看一下这几种概率分布的类型：

正态分布：又叫高斯分布（Gaussian distribution），是最为人们所熟知的分布类型

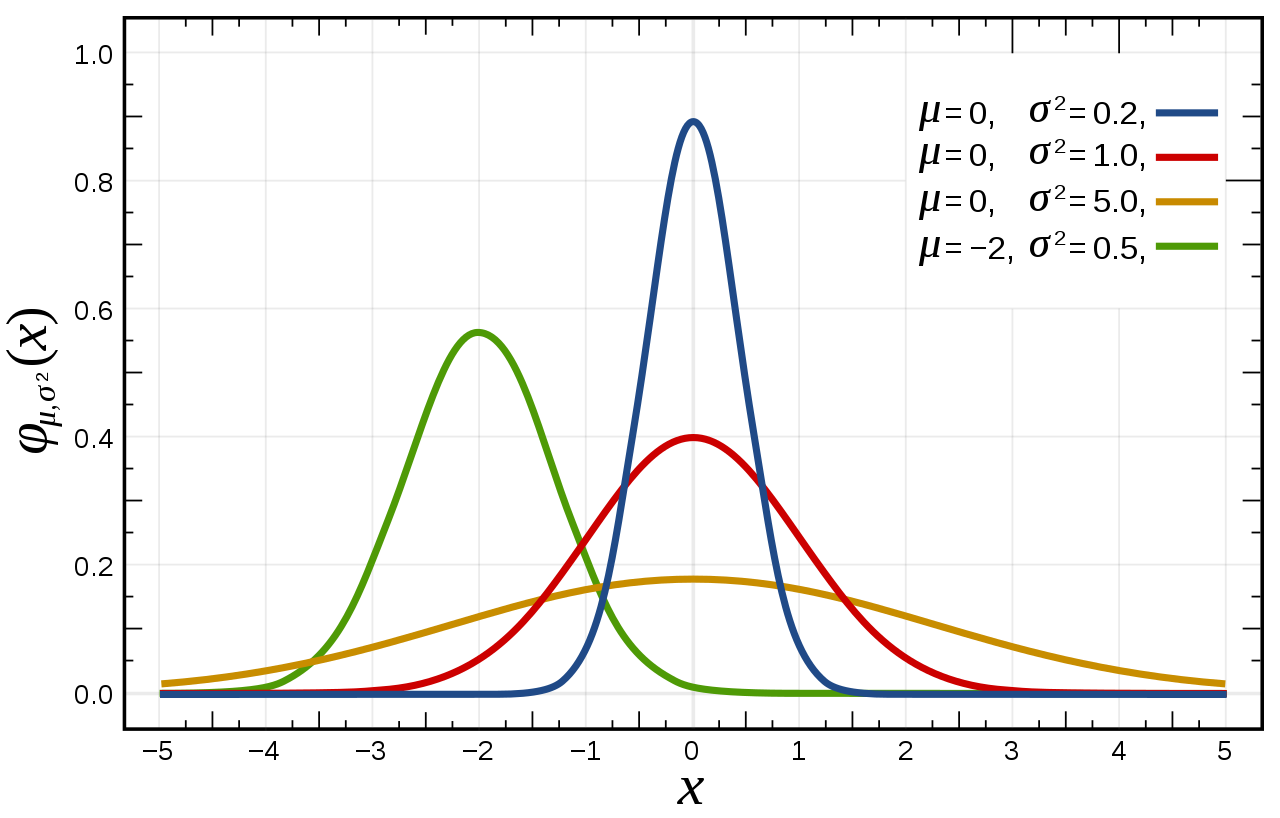
正态分布最为人们所熟知是因为在实际生活中我们经常可以看到正态分布的例子。比如男女身高，学习成绩等都服从正态分布。也就是说身高和学习成绩处于中游水平的人的数量最多，而身高特别高或特别矮以及成绩特别好或特别差的人的数量很少（趋于0），上图的曲线看起来像一口钟，因此正态分布曲线又被称为钟形曲线（bell curve）。

若随机变量X服从一个期望为μ，方差为σ²的正态分布，那么记作X~N(μ，σ²)。正态分布的期望值μ决定了其位置，标准差σ决定了分布的幅度。正态分布的概率密度函数为。

如果数据服从正态分布，我们可以看到大约68%的数据分布在均值的第一个标准差范围之内，95%分布在均值的两个标准差范围之内，99.7%分布在均值的三个标准差范围之内，这就是经验法则（empirical rule）。

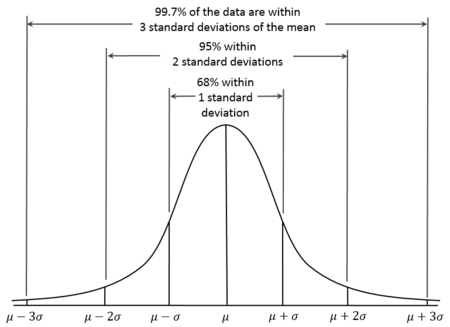
我们可以通过计算随机变量的z值（z score），得知其距离平均值有多少个标准差。z值的计算公式为：。（其中x是随机变量的值，μ是总体均值，σ是总体标准差）

当μ=0，σ=1时，正态分布就成为标准正态分布，记作N（0，1)。通过把服从正态分布的原始数据转变为z值，其z值分布就变为标准正态分布。

通过查找z值表（z-table），我们可以找到z值对应的概率，此概率是z值出现的累计概率（也就是小于此z值的概率）。通过转换，我们就能知道某z值落在某个区间内的概率是多少了。

（如何使用z值表可参考：http://www.z-table.com/how-to-use-z-score-table.html）

我们在实践中为何总是选择使用正态分布呢？正态分布在自然界中的频繁出现只是原因之一，还有一个重要的原因是正态分布的最大熵性质。很多时候，我们并不知道数据的真实分布是什么，我们能从数据中获取到的比较好的知识就是均值和方差，除此之外没有其它更加有用的信息。因此按照最大熵原理，我们应该选择在给定的知识的限制下熵最大的概率分布，而这恰好是正态分布。因此按照最大熵的原理，由于我们对真实分布一无所知，如果数据不能有效提供除了均值和方差之外的更多的知识，即便数据的真实分布不是正态分布，那这时候正态分布就是最佳的选择。（此段摘自正态分布的前世今生）

正态分布的前世今生：

http://songshuhui.net/archives/76501

http://songshuhui.net/archives/77386

t分布：小样本分布

根据中心极限定理，如果从服从正态分布的总体中多次抽样，每次抽取n个观察值，只要抽样次数足够多，那么样本平均数的分布仍然服从正态分布，即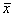~N(μ, )。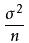

我们可以把这个公式转换一下，变为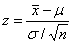，这样计算出某样本均值的z值，就可以找到其对应的累计概率。反过来，我们也可以通过设置置信度（level of confidence），找到相应的z值，然后计算出总体均值的置信区间。

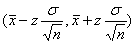但有一个问题，就是在实际应用中，总体的标准差σ往往是未知的，因此人们常用样本标准差s作为σ的估计值。这个问题是解决了，但是还有一个问题。根据样本标准差的计算公式，如果样本中的观察值数量很少，那么样本的标准差就会很大，因此如果在样本量小的情况下直接使用z值公式，得出的结果是不准确的。

那么怎么办呢？有个叫Gosset的人通过计算大量样本均值和样本标准差的比值，得到了这个比值的分布，叫做t分布。

我们按照计算z值的方式，把样本平均数转换成标准值，这个数值就叫做t值（t statistic），t值的分布服从t分布。t值的计算公式为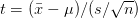：。（其中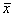是随机样本均值，μ是总体均值，s是样本标准差，n是样本中的观察值数量）

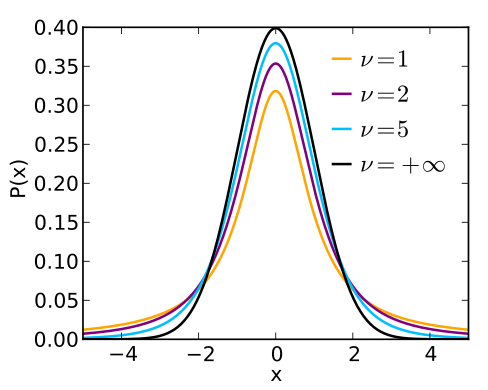
t分布以0为中心，左右对称，其形态变化与自由度ν（degrees of freedom）有关。自由度ν越小，t分布曲线越低平；自由度ν越大，t分布曲线越接近标准正态分布曲线。（自由度指在数据集中能自由变化的观察值的数量，对于某个抽样样本来说，其自由度等于样本中的观察值数量减一，即v=n-1）

我们发现，当样本中的观察值数量接近30时，t分布开始逐渐接近标准正态分布。因此，t分布被广泛使用，因为其不管对于小样本或者大样本都是正确的，而正态分布只对大样本正确。

通过自由度（v）和设置置信度（1-α），在t值表（t-table）上查找出对应的t值。这样，我们可以通过样本均值来对总体均值进行估计（点估计，point estimate），并且可以计算出在某个置信度下（比如95%），总体均值的置信区间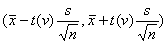（区间估计，interval estimate）。

t分布的发现：

http://www.360doc.com/content/16/1101/21/36719146_603220801.shtml

https://blog.csdn.net/lengxiao1993/article/details/81985399

卡方分布：样本期望值和观察值之间差异的分布

假设O代表某个样本中某个类别的观察频数，E代表基于零假设计算出的期望频数，O与E之差称为残差。残差可以表示某一个类别变量观察值和期望值的偏离程度。但因为残差有正有负，相加后会彼此抵消，因此不能将残差简单相加以表示观察频数与期望频数的差别，为此可以将残差进行平方然后求和。另一方面，残差的大小是一个相对的概念。当期望频数为10时，残差为20显得较大，但当期望频数为1000时，20的残差就很小了。考虑到这一点，人们又将残差平方除以期望频数。对于多个观察值，只要将这些残差平方相加，得到的数值就是χ²值（χ² statistic），χ²值服从卡方分布。χ²值的计算公式为：。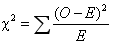

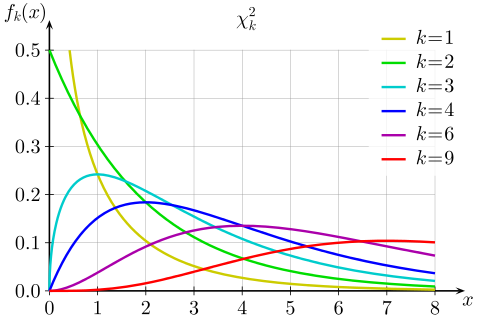
卡方分布的正式定义：若k个相互独立的随机变量服从标准正态分布N（0,1）（也称独立同分布于标准正态分布），则这k个服从标准正态分布的随机变量的平方和构成一个新的随机变量，其分布称为卡方分布（chi-square distribution），自由度为k。

从卡方分布图可以看出：卡方值都是正值，呈右偏态，随着自由度k的增大，其分布趋近于正态分布。（卡方分布的极限就是正态分布）

卡方分布主要用于卡方检验。有两种检验目的，一种是检验样本中各个类别的观察值与期望值是否有显著的不同（goodness of fit），另一种是检验样本中两个类别之间是否相互独立（independence）。

卡方检验的例子：

https://www.jianshu.com/p/807b2c2bfd9b

F分布：多个样本方差比率的分布

t检验和卡方检验可以用来检验单个样本的均值是否和总体一致，或者检验两个样本之间的均值是否一致。那么如果我们需要检验两个以上的样本的均值是否一致该怎么办呢？为此，Fisher创造出了方差分析（analysis of variance，ANOVA），通过分析多个样本的方差来检验这几个样本的均值是否相同。

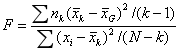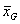将多个样本之间的方差（组间方差）除以样本内部的方差（组内方差），得出的比率被称为F值（F Ratio），F值服从F分布。F值的计算公式为：。（其中是总均值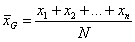，，k是样本数量，N是k个样本的总观察值的数量）

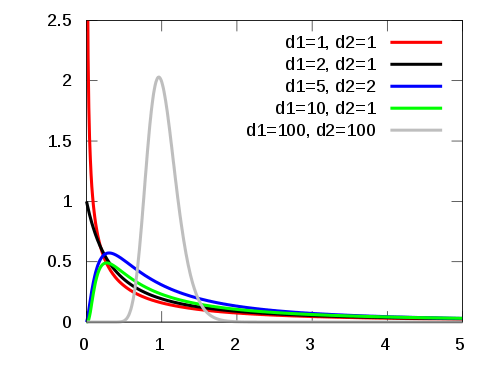
如果组间方差和组内方差相差不大，那么F值应该在1附近，说明这些样本的均值是一致的；如果F值远远大于1，那么说明不是所有的样本均值都是一致的。

F分布的正式定义：假设X、Y为两个独立的随机变量，X服从自由度为n的卡方分布，Y服从自由度为m的卡方分布，这两个独立的卡方分布除以各自的自由度以后的比率服从F分布。

F分布是一种非对称分布，它有两个自由度，即n-1和m-1，相应的分布记为F(n–1，m-1)， n-1通常称为分子自由度， m-1通常称为分母自由度。不同的自由度决定了F分布的形状。