P4013 数字梯形问题 网络流

题目描述

给定一个由 nn 行数字组成的数字梯形如下图所示。

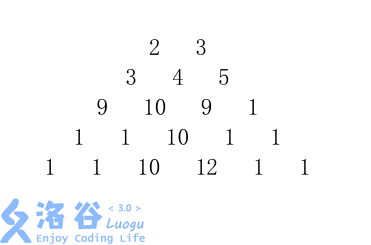
梯形的第一行有 mm 个数字。从梯形的顶部的 mm 个数字开始，在每个数字处可以沿左下或右下方向移动，形成一条从梯形的顶至底的路径。

分别遵守以下规则：

1. 从梯形的顶至底的 mm 条路径互不相交；

2. 从梯形的顶至底的 mm 条路径仅在数字结点处相交；

3. 从梯形的顶至底的 mm 条路径允许在数字结点相交或边相交。

输入输出格式

输入格式：

第 11 行中有 22 个正整数 mm 和 nn，分别表示数字梯形的第一行有 mm 个数字，共有 nn 行。接下来的 nn 行是数字梯形中各行的数字。

第 11 行有 mm 个数字，第 22 行有 m+1m+1 个数字，以此类推。

输出格式：

将按照规则 11，规则 22，和规则 33 计算出的最大数字总和并输出，每行一个最大总和。

输入输出样例

输入样例#1： 复制

2 5
2 3
3 4 5
9 10 9 1
1 1 10 1 1
1 1 10 12 1 1

输出样例#1： 复制

66
75
77

首先声明这是一个比较简单的题目，建图什么的也很容易想，不过我就出现了很多莫名其妙的bug，浪费了很多时间。

有一个bug就是我的第一个out的拆点改成了500然后就错了，这个我现在还是没有明白为什么，但是我觉得呢，这个可能有内部我没有考虑到的原因，所以以后要写的规范一点，不要想当然吧。

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <vector>
#include <string>
#include <algorithm>
#include <iostream>
#include <map>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int maxn = 2e5+;
struct edge
{
    int u, v, c, f, cost;
    edge(int u, int v, int c, int f, int cost) :u(u), v(v), c(c), f(f), cost(cost) {}
};
vector<edge>e;
vector<int>G[maxn];
int a[maxn];//找增广路每个点的水流量
int p[maxn];//每次找增广路反向记录路径
int d[maxn];//SPFA算法的最短路
int inq[maxn];//SPFA算法是否在队列中
int s, t, exa[maxn];
void init()
{
    for (int i = ; i <= maxn; i++)G[i].clear();
    e.clear();
}
void add(int u, int v, int c, int cost)
{
    e.push_back(edge(u, v, c, , cost));
    e.push_back(edge(v, u, , , -cost));
    //printf("%d %d %d %d\n", u, v, c, cost);
    int m = e.size();
    G[u].push_back(m - );
    G[v].push_back(m - );
}
bool bellman(int s, int t, int& flow, int & cost)
{
    memset(d, 0xef, sizeof(d));
    memset(inq, , sizeof(inq));
    d[s] = ; inq[s] = ;//源点s的距离设为0，标记入队
    p[s] = ; a[s] = INF;//源点流量为INF（和之前的最大流算法是一样的）

    queue<int>q;//Bellman算法和增广路算法同步进行，沿着最短路拓展增广路，得出的解一定是最小费用最大流
    q.push(s);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        inq[u] = ;//入队列标记删除
        for (int i = ; i < G[u].size(); i++)
        {
            edge & now = e[G[u][i]];
            int v = now.v;
            if (now.c > now.f && d[v] < d[u] + now.cost)
                //now.c > now.f表示这条路还未流满（和最大流一样）
                //d[v] > d[u] + e.cost Bellman 算法中边的松弛
            {
                // printf("d[%d]=%d d[%d]=%d %d d[%d]=%d\n", v,d[v],u, d[u], now.cost,v,d[u]+now.cost);
                // printf("%d %d %d %d %d %d\n", u, now.u, now.v, now.c, now.f, now.cost);
                d[v] = d[u] + now.cost;//Bellman 算法边的松弛
                p[v] = G[u][i];//反向记录边的编号
                a[v] = min(a[u], now.c - now.f);//到达v点的水量取决于边剩余的容量和u点的水量
                if (!inq[v]) { q.push(v); inq[v] = ; }//Bellman 算法入队
            }
        }
    }
    // printf("a=%d d=%d\n", a[t], d[t]);
    if (d[t] < )return false;//找不到增广路
    flow += a[t];//最大流的值，此函数引用flow这个值，最后可以直接求出flow
    cost += d[t] * a[t];//距离乘上到达汇点的流量就是费用
    // printf("cost=%lld\n", cost);
    for (int u = t; u != s; u = e[p[u]].u)//逆向存边
    {
        e[p[u]].f += a[t];//正向边加上流量
        e[p[u] ^ ].f -= a[t];//反向边减去流量 （和增广路算法一样）
    }
    return true;
}
int Maxflow(int s, int t, int & cost)
{
    cost = ;
    int flow = ;
    while (bellman(s, t, flow, cost));//由于Bellman函数用的是引用，所以只要一直调用就可以求出flow和cost
    return flow;//返回最大流，cost引用可以直接返回最小费用
}
int sum[],cas=;
int n, m;
void out1()
{
    init();
    int len = n;
    for (int i = ; i <= cas; i++) add(i, i + cas, , );//两点之间
    for (int i = ; i <= n; i++) add(s, i, , exa[i]);//源点
    for(int i=;i<m;i++)
    {
        for(int j=;j<=len;j++)
        {
            add(sum[i - ] + j + cas, sum[i] + j, , exa[sum[i] + j]);
            add(sum[i - ] + j + cas, sum[i] + j + , , exa[sum[i] + j + ]);
        }
        len++;
    }
    for (int i = ; i <= m + n - ; i++) add(sum[m - ] + i + cas, t, , );
    int cost = ;
    int ans = Maxflow(s, t, cost);
    printf("%d\n", cost);
}

void out2()
{
    init();
    int len = n;
    for (int i = ; i <= n; i++) add(s, i, , exa[i]);//源点
    for (int i = ; i < m; i++)
    {
        for (int j = ; j <= len; j++)
        {
            add(sum[i - ] + j, sum[i] + j, , exa[sum[i] + j]);
            add(sum[i - ] + j, sum[i] + j + , , exa[sum[i] + j + ]);
        }
        len++;
    }
    for (int i = ; i <= m + n - ; i++) add(sum[m - ] + i, t, inf, );
    int cost = ;
    int ans = Maxflow(s, t, cost);
    printf("%d\n", cost);
    return;
}

void out3()
{
    init();
    int len = n;
    for (int i = ; i <= n; i++) add(s, i, , exa[i]);//源点
    for (int i = ; i < m; i++)
    {
        for (int j = ; j <= len; j++)
        {
            add(sum[i - ] + j, sum[i] + j, inf, exa[sum[i] + j]);
            add(sum[i - ] + j, sum[i] + j + , inf, exa[sum[i] + j + ]);
        }
        len++;
    }
    for (int i = ; i <= m + n - ; i++) add(sum[m - ] + i, t, inf, );
    int cost = ;
    int ans = Maxflow(s, t, cost);
    printf("%d\n", cost);
    return;
}

int main()
{
    cin >> n >> m;
    s = , t = ;
    int len = n;
    for(int i=;i<=m;i++)
    {
        for(int j=;j<=len;j++)
        {
            cin >> exa[cas];
            cas++;
        }
        len++;
    }
    sum[] = ;
    for(int i=;i<=m;i++) sum[i] = sum[i - ] + n + i - ;
    out1();
    out2();
    out3();
    return ;
}