动态规划——leetcode5、最长回文子串
1、题目描述:
2、解题方法:动态规划
动态规划解题步骤:
1、确定状态
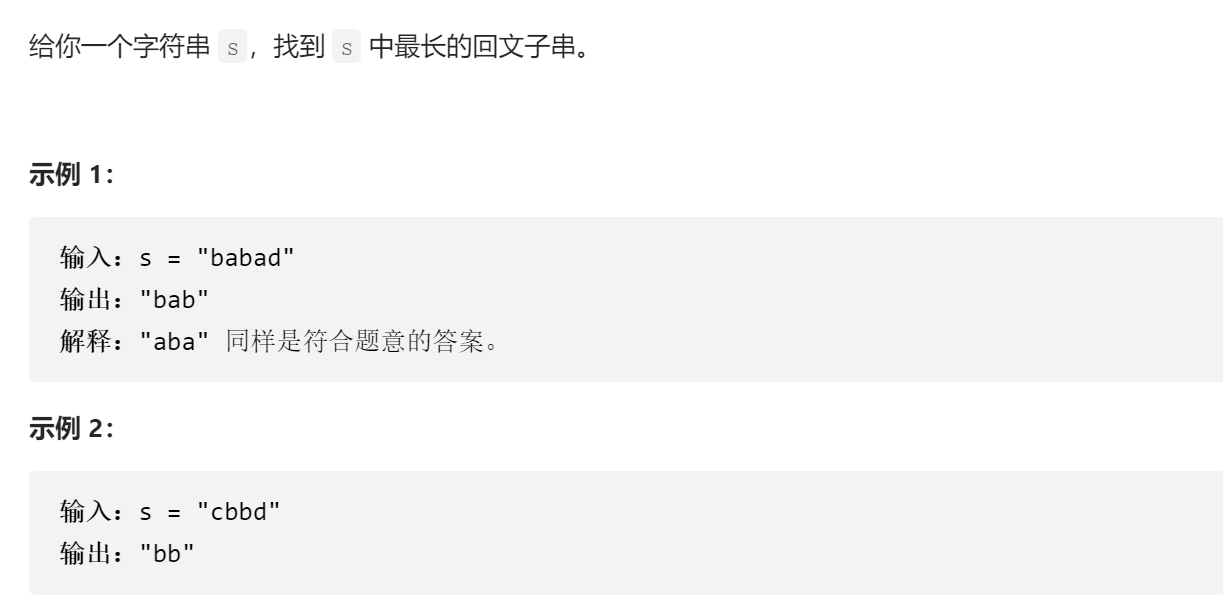
- 最后一步:如果s[i,...,j]是回文子串,那么需要满足两个条件
① s[i] == s[j];
② s[i+1,...,j-1]是回文子串;
- 子问题:我们要验证s[i+1,...,j-1]是不是回文子串
- 用dp[i][j]来表示s[i,...,j]是不是回文子串
2、转移方程
dp[i][j] = (s[i] == s[j])&& dp[i+1][j-1]
3、初始条件和边界情况
初始条件:dp[i][i] == true;
边界条件:在s[i] == s[j]的条件下,j-i<=2或者j-i<3,即说明s[i,...,j]的长度为2或者是3时,不用检查是不是回文串。
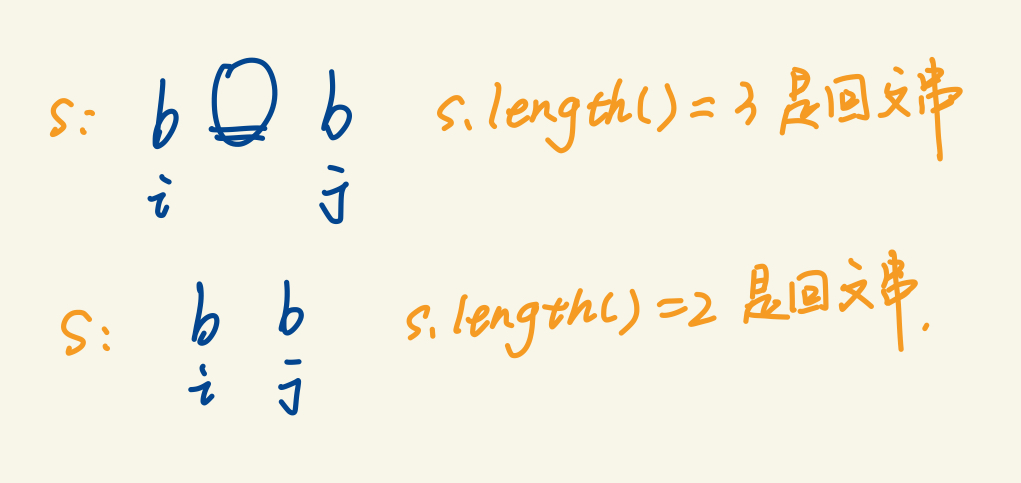
4、计算顺序
以字符串s:babab为例,一列一列的进行填表,先升序填列,再升序填行。
3、代码:
public String longestPalindrome(String s) {
int len = s.length();
if(len < 2){
return s;
}
int maxLen = 1;
int start = 0;
char[] res = s.toCharArray();
boolean[][] dp = new boolean[len][len];
for(int i = 0; i < len; i++){
dp[i][i] = true;
}
for(int j = 1; j < len; j++){
for(int i = 0; i < j; i++){
if(res[i] == res[j]){
if(j - i < 3 || dp[i+1][j-1] == true){
dp[i][j] = true;
}
if( j-i+1 > maxLen && dp[i][j] == true){
maxLen = j-i+1;
start = i;
}
}
}
}
return s.substring(start,start + maxLen);
}
动态规划——leetcode5、最长回文子串的更多相关文章
- leetcode-5 最长回文子串(动态规划)
题目要求: * 给定字符串,求解最长回文子串 * 字符串最长为1000 * 存在独一无二的最长回文字符串 求解思路: * 回文字符串的子串也是回文,比如P[i,j](表示以i开始以j结束的子串)是回文 ...
- LeetCode5 最长回文子串
最长回文子串 给定一个字符串 s,找到 s 中最长的回文子串.你可以假设 s 的最大长度为 1000. 示例 1: 输入: "babad" 输出: "bab" ...
- [Swift]LeetCode5. 最长回文子串 | Longest Palindromic Substring
Given a string s, find the longest palindromic substring in s. You may assume that the maximum lengt ...
- LeetCode5.最长回文子串 JavaScript
给定一个字符串 s,找到 s 中最长的回文子串.你可以假设 s 的最大长度为 1000. 示例 1: 输入: "babad" 输出: "bab" 注意: &qu ...
- 5. Longest Palindromic Substring(最长回文子串 manacher 算法/ DP动态规划)
Given a string s, find the longest palindromic substring in s. You may assume that the maximum lengt ...
- 【LeetCode】最长回文子串【动态规划或中心扩展】
给定一个字符串 s,找到 s 中最长的回文子串.你可以假设 s 的最大长度为 1000. 示例 1: 输入: "babad"输出: "bab"注意: " ...
- Leetcode(5)-最长回文子串(包含动态规划以及Manacher算法)
给定一个字符串 s,找到 s 中最长的回文子串.你可以假设 s 的最大长度为1000. 示例 1: 输入: "babad" 输出: "bab" 注意: &quo ...
- [LeetCode] 5. 最长回文子串 ☆☆☆(最长子串、动态规划)
最长回文子串 (动态规划法.中心扩展算法) https://leetcode-cn.com/problems/longest-palindromic-substring/solution/xiang- ...
- leetcode5 最长回文字符串 动态规划 Manacher法
dp 注意没有声明S不空,处理一下 o(n^2) class Solution { public: string longestPalindrome(string s) { if (s.empty() ...
- [译]最长回文子串(Longest Palindromic Substring) Part I
[译]最长回文子串(Longest Palindromic Substring) Part I 英文原文链接在(http://leetcode.com/2011/11/longest-palindro ...
随机推荐
- ThreadLocal模板
public class UserIdThreadLocal { private static final ThreadLocal<Long>LOCAL=new ThreadLocal&l ...
- 【实操干货】做好这 16 项优化,你的 Linux 操作系统焕然一新
大家好,这次跟大家谈谈又拍云的操作系统优化方案.往简单地说,我们使用的 Linux 操作系统主要都是基于 CentOS6/7 的精简和优化.往复杂地说,则是我们有两套系统,业务上使用的定制 Linux ...
- 基于Kubernetes v1.24.0的集群搭建(一)
一.写在前面 K8S 1.24作为一个很重要的版本更新,它为我们提供了很多重要功能.该版本涉及46项增强功能:其中14项已升级为稳定版,15项进入beta阶段,13项则刚刚进入alpha阶段.此外,另 ...
- Ubuntu Linux处理Waiting for cache lock: Could not get lock /var/lib/dpkg/lock-frontend. It is held by process 3365 (unattended-upgr)问题
问题 在Ubuntu中,执行apt install后,出现以下问题: Waiting for cache lock: Could not get lock /var/lib/dpkg/lock-fro ...
- 在海思芯片上使用GDB远程调试
1 前言 使用海思平台上(编译工具链:arm-himix200-linux)交叉编译 GDB 工具(使用版本8.2,之前用过10.2的版本,在编译 gdbserver 遇到编译出错的问题,因为关联了其 ...
- Windows家庭版-添加Hyper-V
新建一个hyper-v.cmd文件,内容为 pushd "%~dp0" dir /b %SystemRoot%\servicing\Packages\*Hyper-V*.mum & ...
- Maven + SSM环境搭建
Maven + SSM 之前Maven+SSM都是照着搭建的,自己想写点什么的时候发现搭建的过程不清楚. 于是花了时间边整理思路边搭建,并把搭建过程记录下来. 视频看来终觉浅,还是需要自己动手实践,捋 ...
- Linux IO重定向和管道
计算机组成部分: 由io . 控制器.计算器.存储器组成 IO: input output 计算机里面通过终端窗口实现输入和输出,键盘鼠标屏幕这些只是手段,真正完成输入输出的是终端窗口 标准输入.出. ...
- 深入解析kubernetes controller-runtime
Overview controller-runtime 是 Kubernetes 社区提供可供快速搭建一套 实现了controller 功能的工具,无需自行实现Controller的功能了:在 Kub ...
- centos7 离线升级/在线升级操作系统内核
目录 一.前言 二.系统环境 三.系统内核下载网址 四.centos7离线升级系统内核 1.先查看系统环境 2.离线升级系统内核 五.在线升级系统内核 一.前言 CentOS(Community EN ...
