ML-L1、L2 正则化

出现过拟合时，使用正则化可以将模型的拟合程度降低一点点，使曲线变得缓和。

L1正则化（LASSO）

正则项是所有参数的绝对值的和。正则化不包含theta0，因为他只是偏置，而不影响曲线的摆动幅度。

\[J(\theta)=\operatorname{MSE}(y, \hat{y})+\alpha \sum_{i=1}^{n}\left|\theta_{i}\right|
\]

# 使用pipeline进行封装
from sklearn.linear_model import Lasso
# 使用管道封装lasso
def LassoRegssion(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree = degree)),
        ("std_scaler", StandardScaler()),
        ("lasso", Lasso(alpha=alpha))
    ])

使用\(\alpha=0.01\) 的正则化拟合20阶多项式

lasso_reg = LassoRegssion(20, 0.01)
lasso_reg.fit(X_train, y_train)
y_predict = lasso_reg.predict(X_test)

plot_model(lasso_reg)

MSE 1.149608084325997

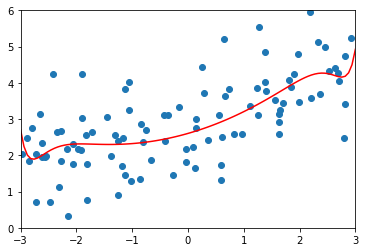
\(\alpha=0.1\)

MSE 1.1213911351818648

\(\alpha=1\) 时，均方误差又变大了，正则化过度了。模型变成了直线，所有参数都接近0了。因为没有对\(\theta_0\)进行正则化，所以偏置的值没有变化

1.8408939659515595

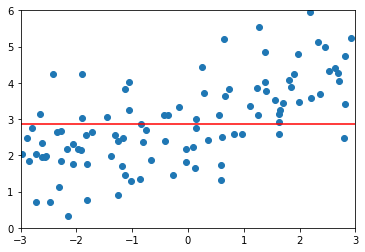
L2正则化（岭回归）

1/2可加可不加，因为方便求导。对J()求最小值时，也将\(\theta\)的值变小。当\(\alpha\)越大，右边受到的影响就越大，\(\theta\)的值就越小

\[J(\theta)=\operatorname{MSE}(y, \hat{y})+\alpha \frac{1}{2} \sum_{i=1}^{n} \theta_{i}^{2}
\]

使用pipeline封装Ridge

from sklearn.linear_model import Ridge
# 使用管道封装岭回归
def RidgeRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree = degree)),
        ("std_scaler", StandardScaler()),
        ("ridge_reg", Ridge(alpha = alpha))
    ])

使用20阶多项式拟合，\(\alpha=0\)即没有正则化。

ridge_reg100 = RidgeRegression(20, 0)
ridge_reg100.fit(X_train, y_train)
y_predict = ridge_reg100.predict(X_test)
plot_model(ridge_reg100)

# MSE 167.94010860994555

\(\alpha=0.0001\)

ridge_reg100 = RidgeRegression(20, 0.0001)

# MSE 1.3233492754136291

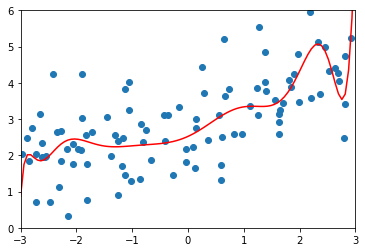
\(\alpha=10\)

ridge_reg100 = RidgeRegression(20, 10)

# MSE 1.1451272194878865

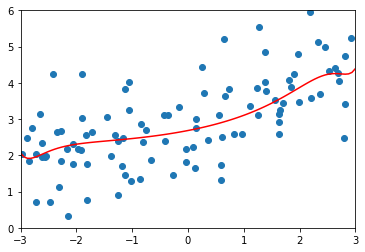
\(\alpha=1000\)

ridge_reg100 = RidgeRegression(20, 10000)

# MSE 1.7967435583384

对比

• LASSO更趋向于将一部分参数变为0，更容易得到直线。Ridge更容易得到曲线。
• \(\alpha\)越大，正则化的效果越明显

两个正则化的不同仅仅在于正则化项的不同：

\[J(\theta)=\operatorname{MSE}(y, \hat{y})+\alpha \sum_{i=1}^{n}\left|\theta_{i}\right|
\]

\[J(\theta)=\operatorname{MSE}(y, \hat{y})+\alpha \frac{1}{2} \sum_{i=1}^{n} \theta_{i}^{2}
\]

常见的对比还有：

MSE 和 MAE :

\[MSE ==> \frac{1}{n} \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}
\]

\[MAE ==> \frac{1}{n} \sum_{i=1}^{n}\left|y_{i}-\hat{y}_{i}\right|
\]

欧拉距离和曼哈顿距离：

\[\sqrt{\sum_{i=1}^{n}\left(x_{i}^{(1)}-x_{i}^{(2)}\right)^{2}} 和 \sum_{i=1}^{n}\left|x_{i}^{(1)}-x_{i}^{(2)}\right|
\]

还有明可夫斯基距离：

\[\left[\sum_{i=1}^{n}\left|X_{i}^{(a)}-X_{i}^{(b)}\right|^{p}\right]^{\frac{1}{p}}
\]

弹性网（待定）

就是将两个范式进行结合。

\[J(\theta)=\operatorname{MSE}(y, \hat{y})+r \alpha \sum_{i=1}^{n}\left|\theta_{i}\right|+\frac{1-r}{2} \alpha \sum_{i=1}^{n} \theta_{i}^{2}
\]