NOI / 2.1基本算法之枚举-8760:Cantor表

总时间限制:

1000ms

内存限制:

65536kB

描述

现代数学的著名证明之一是Georg Cantor证明了有理数是可枚举的。他是用下面这一张表来证明这一命题的：

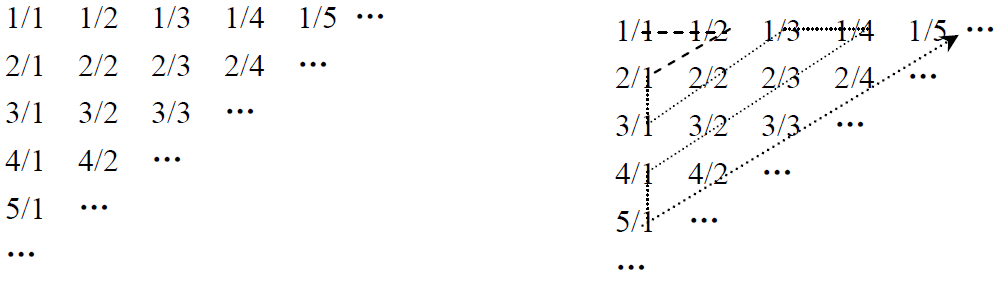
我们以Z字形给上表的每一项编号。第一项是1/1，然后是1/2，2/1，3/1，2/2，…

给定N，求第N项。

输入

一个整数N（1≤N≤10000000）。

输出

一个分数，即表中的第N项。

样例输入

7

样例输出

1/4

来源

NOIP1999复赛 普及组 第一题

参考代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,i,j,h=1,t=0;//H,T要给初值
	cin>>n;
	while(1)//条件永远为真
	{
		for(i=1,j=h;i<=h&&j>=1;i++,j--)
		{
			t++;
			if(t==n)
			{
				if(h%2==1)
				cout<<j<<"/"<<i;
				else
				cout<<i<<"/"<<j;
				return 0;//直接结束程序
			}
		}
		h++;
	}
	return 0;
}