机器学习 —— log-linear 模型

　　昨天刚刚解决了 logistic regression 之后今天又来了个有趣的家伙。 logistic regression 很强大，但是也有它的弱点。它最大的弱点就是只能告诉你是或者不是，而无法告诉你 XX is YY.这对于追求人工智能来说，只能是走出了一小步。在解决 YES/NO 的问题之后，我们还需要解决 WHAT 这个问题。 聪明的计算机科学家（也许是数学家）又设计了一种新的模型，这种模型可以告诉我们 WHAT。也就是 log-linear 模型。

——离真正的人工智能还很远，或许它是一个科学问题而不是一个工程问题，记我学习 Mechine Learning 的第二天

1、Log-linear

　　如果要计算机告诉我们WHAT，按照之前的思路，还是应该从概率入手。应该是找到某个模型，模型的输入是一些信息，模型的输出是the label在已知信息下的可能性。这个模型里有参数，不同的label对应不同的参数。对于测试目标，我们只要比较它-->model(the para) 后得到的概率，就可以推断它和哪个label比较配。label应该是有限的。接下来的任务就是找the label 对应的参数。

　　这组参数应该使 p(y|x;w)达到最大，其中 y 是what：洗衣机，台灯，冰箱、、、、x 是样本：颜色，形状，大小，重量，价格，材质......

　　概念我们有了，接下来就只有一个问题：这个模型长什么样。既然是个概率模型，那我觉得首先有两个重要特征：

　　1.它应该不只一项，最好每项都能表达 <label - 维度> ，样本有d个维度，这个方程应该有 d 项，毕竟我们总是希望我们的各种样本维度在计算时不是耦合的。

　　2.它的取值范围应该在0~1之间，因为它是概率。

　　接下来我们就要设计一个有着优良数学性质的模型，毕竟我们还要对参数求导算梯度呢。。。。搞个很复杂的东西怎么行。。。。

　　首先，这次的方程不再是x一个人的事情，因为y也是多样的：那么对于某一项应该表示成: Fij(x_i,y_1).

　　其次，这些项应该是相加关系，我们用权重来控制这一项对 p(y_j|x)的贡献， 也就是说，这些项的“合成效果”应该表达成 ：Wij是各个项的权重.

i = 1:d  j=1

∑Wij*Fij(x_i,y_j) 

　　接下来，上面那一堆和的结果都不一定是正的，所以我们首先要保证它大于0，老办法取指数: exp(∑Wij*Fij(x_i,y_j))

　　最后，如果再想办法让整个东西小于1，那它就基本符合我们的要求了，怎么搞? 显然，把所有词性都算一遍再求和，就会大于单个词性。

　　实际上，我们拼出来的就是log-linear模型。

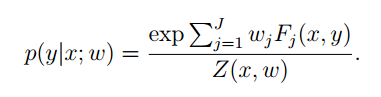
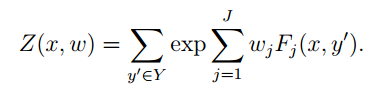
　　那么在给定一个训练集时，我们要使得the label判断最准确，应该让p尽量大。本质上就是让分子尽量大，我们就有了训练的目标：

　　

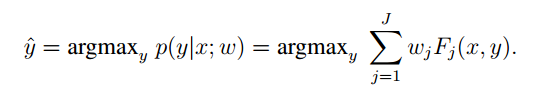
　　于是乎还剩下最后一个问题，如何确定 F

2.特征方程 F

　　F 被称为特征方程，它一共有 C*d个，C是标签数，d是样本维度。也就是说，每个维度都是和特征有关的。

　　

　　

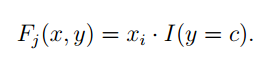
i=1~d, c=1~C

　　　　也就是说，Fj对应了所有的label,每个label 有d个F. 是不同的。这样可以自动生成需要的所有Fj（洗衣机对应1~d号的话,电吹风会自动对应d+1~2d号。。。），上述是一种Naive的Fj设置方法，它认为只有当y取某个特定标签时，才使用Fj中的某些项，当y取其他标签时，这组权重是被屏蔽的。例如：我们在讨论某个物体是不是洗衣机时，电吹风的训练权重就被屏蔽了。这本质上就是很多很多logistic regression 并联在一起。

　　为了方便使用，做以下设计：F--->0/1。很好理解，某个标签和某个样本维度要么有关要么无关，至于最后会是多少由权重调节。

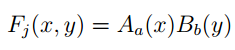
　　这里是为一个词进行词性判别，A1~A4是和名词判别有关的Function这里的B(名词)就应该全部取1，选通A1~A4,屏蔽其他

　　A5~A8可能会是和动词有关的判别了，如果y=动词 被选通，则屏蔽和名词，形容词等有关的判别。