数据结构笔记--二叉查找树概述以及java代码实现

一些概念:

　　二叉查找树的重要性质:对于树中的每一个节点X,它的左子树任一节点的值均小于X,右子树上任意节点的值均大于X.

　　二叉查找树是java的TreeSet和TreeMap类实现的基础.

　　由于树的递归定义,二叉查找树的代码实现也基本上都是使用递归的函数,二叉查找树的平均深度是O(logN).

　　因为二叉查找树要求所有的节点都可以进行排序.所以编写时代码时需要一个Comparable泛型接口,当需要对类中的对象进行排序的时候,就需要实现这个泛型接口,里边定义了一个public int compareTo(Object o)方法,接受一个Object作为参数,java中String,Integer等类都实现了这个接口.

java代码实现:

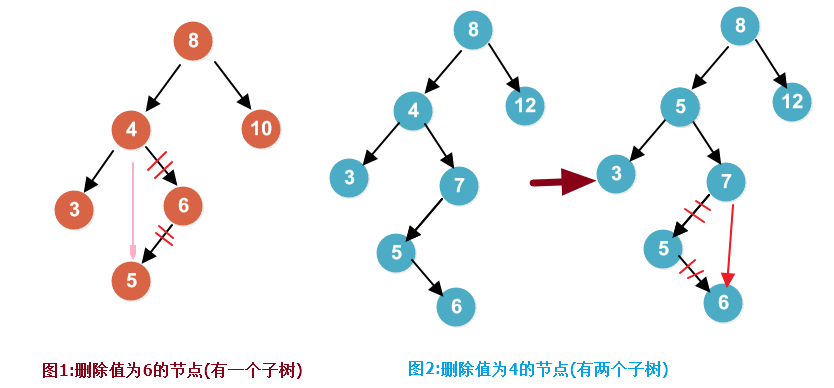
　　remove方法:在查找树的代码实现中,最难得是删除,因为这涉及到三种情况:

　　　　被删除节点是树叶节点(没有子树):最简单,直接删除,将该节点置为null即可

　　　　被删除节点有一个子节点(左子树或右子树):是该节点的父节点指向该节点的子节点(左或右).见图1

　　　　被删除节点有两个子节点:用其右子树中的最小值代替该节点上的值,删除其右子树上的最小值.见图2.

　　

 package com.wang.tree;

 public class BinarySearchTree<T extends Comparable<T>>{

     private static class Node<T>{
         private T data;
         private Node<T> left;
         private Node<T> right;

         public Node(T data){
             this(data,null,null);
         }
         public Node(T data, Node<T> left, Node<T> right) {
             this.data = data;
             this.left = left;
             this.right = right;
         }
     }

     //私有变量 根节点root
     private Node<T> root;

     //无参构造函数,根节点为null
     public BinarySearchTree(){
         root=null;
     }

     //清空二叉查找树
     public void makeEmpty(){
         root=null;
     }
     //判断树是否为空
     public boolean isEmpty(){

         return root==null;
     }
     //查找集合中是否有元素value,有返回true
     public boolean contains(T value){

         return contains(value,root);
     }

     private boolean contains(T value, Node<T> t) {

         if(t==null){
             return false;
         }
         int result=value.compareTo(t.data);
         if(result<0){
             return contains(value,t.left);
         }else if(result>0){
             return contains(value,t.right);
         }else{
             return true;
         }
     }

     //查找集合中的最小值
     public T findMin(){

         return  findMin(root).data;
     }
     private Node<T> findMin(Node<T> t) {
         if(t==null){
             return null;
         }else if(t.left==null){
             return t;
         }

         return findMin(t.left);
     }

     //查找集合中的最大值
     public T findMax(){

         return findMax(root).data;
     }

     private Node<T> findMax(Node<T> t) {
         if(t!=null){
             while(t.right!=null){
                 t=t.right;
             }
         }

         return t;
     }

     //插入元素
     public void insert(T value){

         root =insert(value,root);
     }

     private Node<T> insert(T value, Node<T> t) {
         if(t==null){
             return new Node(value,null,null);
         }
         int result=value.compareTo(t.data);
         if(result<0){
             t.left=insert(value,t.left);
         }else if(result>0){
             t.right=insert(value,t.right);
         }
         return t;
     }
     //移除元素
     public void remove(T value){
         root=remove(value,root);

     }

     private Node<T> remove(T value, Node<T> t) {
         if(t==null){
             return t;
         }

         int result=value.compareTo(t.data);
         if(result<0){
             t.left=remove(value,t.left);
         }else if(result>0){
             t.right=remove(value,t.right);
         }else if(t.left!=null&&t.right!=null){//如果被删除节点有两个儿子
             //1.当前节点值被其右子树的最小值代替
             t.data=findMin(t.right).data;
             //将右子树的最小值删除
             t.right=remove(t.data, t.right);
         }else{
             //如果被删除节点是一个叶子 或只有一个儿子
             t=(t.left!=null)?t.left:t.right;
         }

         return t;
     }

     //中序遍历打印
     public void printTree(){
         printTree(root);
     }

     private void printTree(Node<T> t) {

         if(t!=null){
             printTree(t.left);
             System.out.println(t.data);
             printTree(t.right);
         }
     }
 }

　　测试代码:

package com.wang.tree;

public class TestBST {

    public static void main(String[] args) {

        BinarySearchTree<Integer> bst=new BinarySearchTree<>();
        bst.insert(5);
        bst.insert(7);
        bst.insert(3);
        bst.insert(1);
        bst.insert(9);
        bst.insert(6);
        bst.insert(4);
        System.out.println("最小值:"+bst.findMin());
        System.out.println("最大值:"+bst.findMax());
        System.out.println("查找元素9是否存在:"+bst.contains(9));
        System.out.println("查找元素8是否存在:"+bst.contains(8));
        System.out.println("遍历二叉树");
        bst.printTree();
    }
}

打印结果:

最小值:1
最大值:9
查找元素9是否存在:true
查找元素8是否存在:false
遍历二叉树
1
3
4
5
6
7
9