(简单) POJ 3076 Sudoku , DLX+精确覆盖。

　　Description

　　A Sudoku grid is a 16x16 grid of cells grouped in sixteen 4x4 squares, where some cells are filled with letters from A to P (the first 16 capital letters of the English alphabet), as shown in figure 1a. The game is to fill all the empty grid cells with letters from A to P such that each letter from the grid occurs once only in the line, the column, and the 4x4 square it occupies. The initial content of the grid satisfies the constraints mentioned above and guarantees a unique solution. 
 
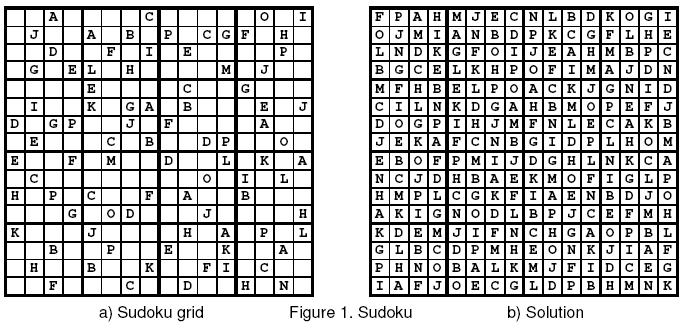
　　Write a Sudoku playing program that reads data sets from a text file.

 

　　这个题和POJ 3076没有什么区别，不过就是要注意一个问题，就是MaxNode不要太大，不然的话会MLE，对于数组不用开到MaxN*MaxM这么大，因为数独的很多方格都已经填上了，根本用不了那么大。。。。。。

 

　　然后还要注意格式的问题，答案是要空行的。。。。。。

 

代码如下：

#include<iostream>
#include<cstring>
#include<cstdio>

using namespace std;

const int MaxN=**+;
const int MaxM=**+;
const int MaxNode=MaxN*MaxM/;

int cas=;

struct DLX
{
    int U[MaxNode],D[MaxNode],L[MaxNode],R[MaxNode],col[MaxNode],row[MaxNode];
    int size,n,m;
    int H[MaxN],S[MaxM];
    int ans[*+],ans1[*+];

    void init(int _n,int _m)
    {
        n=_n;
        m=_m;

        for(int i=;i<=m;++i)
        {
            U[i]=D[i]=i;
            L[i]=i-;
            R[i]=i+;
            row[i]=;

            S[i]=;
        }
        L[]=m;
        R[m]=;

        size=m;

        for(int i=;i<=n;++i)
            H[i]=-;
    }

    void Link(int r,int c)
    {
        col[++size]=c;
        row[size]=r;
        ++S[c];

        U[size]=U[c];
        D[size]=c;
        D[U[c]]=size;
        U[c]=size;

        if(H[r]==-)
            H[r]=L[size]=R[size]=size;
        else
        {
            L[size]=L[H[r]];
            R[size]=H[r];
            R[L[H[r]]]=size;
            L[H[r]]=size;
        }
    }

    void remove(int c)
    {
        L[R[c]]=L[c];
        R[L[c]]=R[c];

        for(int i=D[c];i!=c;i=D[i])
            for(int j=R[i];j!=i;j=R[j])
            {
                U[D[j]]=U[j];
                D[U[j]]=D[j];
                --S[col[j]];
            }
    }

    void resume(int c)
    {
        for(int i=U[c];i!=c;i=U[i])
            for(int j=L[i];j!=i;j=L[j])
            {
                U[D[j]]=j;
                D[U[j]]=j;
                ++S[col[j]];
            }

        L[R[c]]=R[L[c]]=c;
    }

    void showans(int d)
    {
        if(cas!=)
            cout<<endl;

        for(int i=;i<d;++i)
            ans1[(ans[i]-)/+]=(ans[i]-)%+;

        for(int i=;i<=;++i)
        {
            cout<<char(ans1[i]-+'A');

            if(i%==)
                cout<<endl;
        }

        ++cas;
    }

    bool Dance(int d)
    {
        if(R[]==)
        {
            showans(d);
            return ;
        }

        int c=R[];

        for(int i=R[];i!=;i=R[i])
            if(S[i]<S[c])
                c=i;

        remove(c);

        for(int i=D[c];i!=c;i=D[i])
        {
            ans[d]=row[i];

            for(int j=R[i];j!=i;j=R[j])
                remove(col[j]);

            if(Dance(d+))
                return ;

            for(int j=L[i];j!=i;j=L[j])
                resume(col[j]);
        }

        resume(c);

        return ;
    }

    void display()
    {
        for(int i=R[];i!=;i=R[i])
        {
            cout<<i<<' ';
            for(int j=D[i];j!=i;j=D[j])
                cout<<'('<<j<<','<<(row[j]-)%+<<')'<<' ';

            cout<<endl;
        }
    }
};

DLX dlx;
char s[];

void getchange(int &r,int &c1,int &c2,int &c3,int &c4,int i,int j,int k)
{
    r=(i*+j)*+k;
    c1=i*+j+;
    c2=+i*+k;
    c3=+j*+k;
    c4=+((i/)*+(j/))*+k;
}

void slove()
{
    int r,c1,c2,c3,c4;

    dlx.init(**,**);

    for(int i=;i<;++i)
        for(int j=;j<;++j)
            for(int k=;k<=;++k)
                if(s[i*+j]=='-' || s[i*+j]-'A'+==k)
                {
                    getchange(r,c1,c2,c3,c4,i,j,k);

                    dlx.Link(r,c1);
                    dlx.Link(r,c2);
                    dlx.Link(r,c3);
                    dlx.Link(r,c4);
                }

/*    for(int i=1;i<=256;++i)
        for(int j=1;j<=16;++j)
            if(s[i-1]=='-' || (j+(i-1)*16-1)%16+1==s[i-1]-'A'+1)
                dlx.Link(j+(i-1)*16,i);

    for(int i=1;i<=256;++i)
        for(int j=1;j<=16;++j)
            if(s[i-1]=='-' || (16*(j-1)+(i-1)%16+1+256*((i-1)/16)-1)%16+1==s[i-1]-'A'+1)
                dlx.Link(16*(j-1)+(i-1)%16+1+256*((i-1)/16),i+256);

    for(int i=1;i<=256;++i)
        for(int j=1;j<=16;++j)
            if(s[i-1]=='-' || ((j-1)*256+i-1)%16+1==s[i-1]-'A'+1)
                dlx.Link((j-1)*256+i,i+512);

    for(int i=1;i<=4;++i)
        for(int j=1;j<=4;++j)
            for(int k=1;k<=16;++k)
                for(int l=1;l<=4;++l)
                    for(int m=1;m<=4;++m)
                        if(s[(i-1)*64+(j-1)*16+k-1]=='-' || ((i-1)*1024+(j-1)*64+k+(l-1)*256+(m-1)*16-1)%16+1==s[(i-1)*64+(j-1)*16+k-1]-'A'+1)
                            dlx.Link((i-1)*1024+(j-1)*64+k+(l-1)*256+(m-1)*16,(i-1)*64+(j-1)*16+k+768);

    for(int i=0;i<256;++i)
        if(s[i]!='-')
        {
            dlx.ans1[i+1]=s[i]-'A'+1;

            dlx.remove(i+1);

            for(int j=dlx.D[i+1];j!=i+1;j=dlx.D[j])
            {
                if((dlx.row[j]-1)%16+1==s[i]-'A'+1)
                {
                    for(int k=dlx.R[j];k!=j;k=dlx.R[k])
                        dlx.remove(dlx.col[k]);

                    break;
                }
            }
        }
*/
    dlx.Dance();
}

int main()
{
    ios::sync_with_stdio(false);

    char st[];

    while(cin>>s)
    {
        for(int i=;i<;++i)
        {
            cin>>st;
            strcat(s,st);
        }

        slove();
    }

    return ;
}