poj 2594 Treasure Exploration（最小路径覆盖，可重点）

　　题意：选出最小路径覆盖图中所有点，路径可以交叉，也就是允许路径有重复的点。

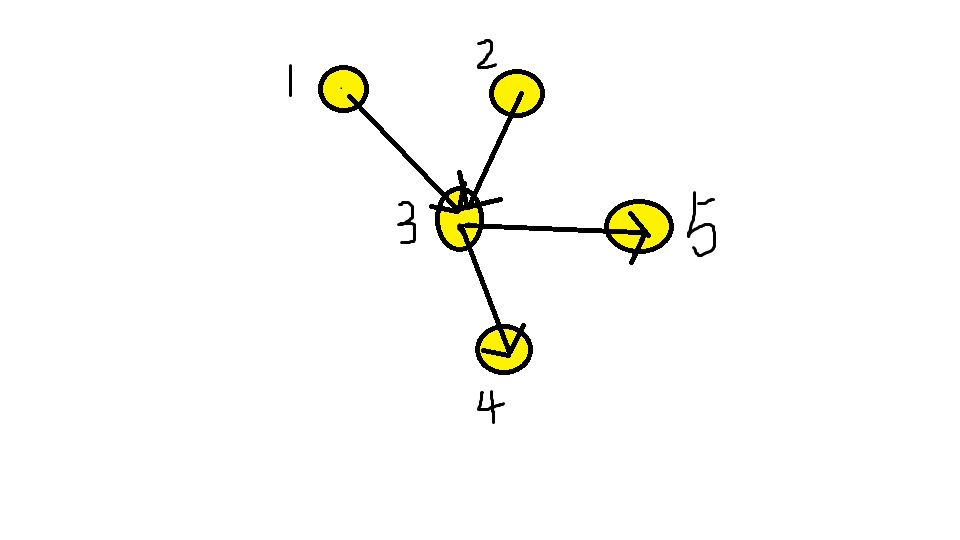
　　分析：这个题的难点在于如何解决有重复点的问题～方法就是使用Floyd求闭包，就是把间接相连的点直接连上边，然后就是求最小路径覆盖了。我来大概解释一下为什么是对的，首先我们要明确，当我们重复利用一个点的时候，一定是有两个比较良好的路径相交了，而二分图是不允许这样的情况存在的，因为那必然存在了一个点有一个以上的出度或者入度了，而怎么避免这个问题呢，看下面的图：

　　这就是针对这个问题的一个典型的模型，如果使用正常二分图，求得的匹配值为2，路径数为3（例如：2-3-5，1，4），但是如果我们把3用两次，那么求得的答案就是2了（例如：2-3-5，1-3-4）.

so，我们的解决办法就出来了，当（2-3-5）这个路径被选择的时候，我们在（1-3-4）这个路径时只要把3无视掉，直接在1-4之间建一条边就可以了，那样1-4就匹配成功了。这样所有含有交叉点的路径，都可以先选择一个路径，然后直接跨过交叉点连接一个，它所代表的仍然是经过交叉点的路径。

　　有人也许会问，Floyd会压缩所有的边，会不会导致错误呢？ 不会，比如这个图（1-4）和（1-5）都有边，在匹配中二分图是最大匹配，他会优先获得较多的匹配，最后无法找到增广路，才会考虑我们连接的边，不要因为边都被压缩了有一种答案会变小的错误。代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define maxn 510
int maps[maxn][maxn],vis[maxn],link[maxn];
int n,m;
void floyd()
{
    for(int i = ; i <= n; i++)
    {
        for(int j = ; j <= n; j++)
        {
            if(!maps[i][j])
            {
                for(int k = ; k <= n; k++)
                {
                    if(maps[i][k] && maps[k][j])
                    {
                        maps[i][j] = ;
                        break;
                    }
                }
            }
        }
    }
}
bool dfs(int u)
{
    for(int i = ; i <= n; i++)
    {
        if(maps[u][i] && !vis[i])
        {
            vis[i] = ;
            if(link[i] == - || dfs(link[i]))
            {
                link[i] = u;
                return true;
            }
        }
    }
    return false;
}
int slove()
{
    int ans = ;
    memset(link,-,sizeof(link));
    for(int i = ; i <= n; i++)
    {
        memset(vis,,sizeof(vis));
        if(dfs(i)) ans++;
    }
    return ans;
}
int main()
{
    int x,y;
    while(~scanf("%d%d",&n,&m))
    {
        if(!n && !m) break;
        memset(maps,,sizeof(maps));
        while(m--)
        {
            scanf("%d%d",&x,&y);
            maps[x][y] = ;
        }
        floyd();
        printf("%d\n",n-slove());
    }
    return ;
}