机器学习——利用PCA来简化数据

降维技术的好处：

　　1.使得数据集更易使用

　　2.降低很多算法的计算开销

　　3.取出噪声

　　4.使得结果易懂

在已标注和未标注的数据上都有降维技术，降维的方法：

　　1.主成分分析（Principal Component Analysis，PCA）。在PCA中，数据从原来的坐标系转换到新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。该过程中一直重复，重复次数为原始数据中特征的数目。我们会发现，大部分方差都包含在最前面的几个新坐标轴中。因此，我们就可以忽略余下的坐标轴，即对数据进行了降维处理。

　　2.因子分析（Factor Analysis）。在因子分析中，我们假设在观察数据的生成中有一些观察不到的隐变量（latent variable）。假设观察数据是这些隐变量和某些噪声的线性组合。那么隐变量的数据可能比观察数据的数目少，也就是说通过找到隐变量就可以实现数据的降维。

　　3.独立成分分析（Independent Component Analysis，ICA）。ICA假设数据是从N个数据源生成的，这一点和因子分析有些类似。假设数据为多个数据源的混合观察结果，这些数据源之间在统计上相互独立的，而在PCA中只假设数据是不相关的。同因子分析一样，如果数据源的数目少于观察数据的数目，则可以实现降维过程。

主成分分析

优点：降低数据的复杂度，识别最重要的多个特征

缺点：不一定需要，且可能损失有用信息

适用数据类型：数值型数据

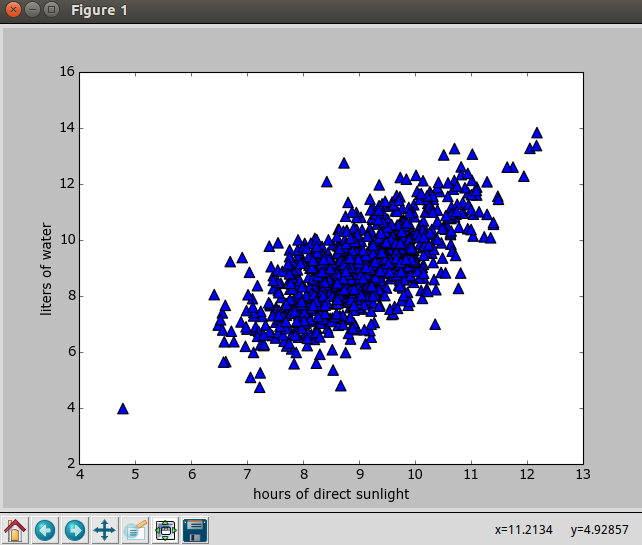
对于下图中的二维数据，这个二维数据是随机生成的

# coding:utf-8
# !/usr/bin/env python

'''
Created on Jun 1, 2011

@author: Peter
'''
from numpy import *
import matplotlib
import matplotlib.pyplot as plt

n = 1000 		#number of points to create
xcord0 = []
ycord0 = []
xcord1 = []
ycord1 = []
markers =[]
colors =[]
fw = open('testSet.txt','w')
for i in range(n):
    [r0,r1] = random.standard_normal(2)		#随机生成一组二维数据(fFlyer,tats)
    fFlyer = r0 + 9.0
    tats = 1.0*r1 + fFlyer + 0
    xcord0.append(fFlyer)
    ycord0.append(tats)
    fw.write("%f\t%f\n" % (fFlyer, tats))	#将二维数据(fFlyer,tats)写入文件中

fw.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord0,ycord0, marker='^', s=90)
plt.xlabel('hours of direct sunlight')
plt.ylabel('liters of water')
plt.show()

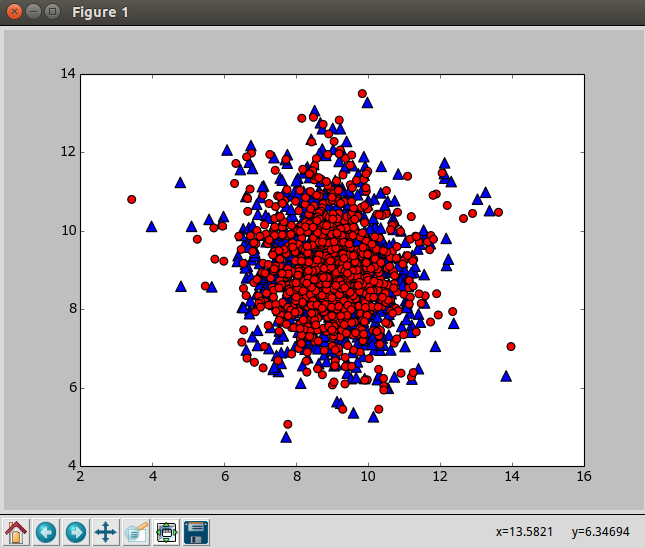
使用下面的程序对二维数据进行主成分分析，输出原始数据重构之后的矩阵lowDDataMat(蓝色)，第一主成分reconMat(红色)

def pca(dataMat, topNfeat=9999999):				#数据矩阵, 输出前topNfeat个特征，如果topNfeat=1就是降维成1维
    meanVals = mean(dataMat, axis=0)			#求平均值
    meanRemoved = dataMat - meanVals 			#去除平均值
    covMat = cov(meanRemoved, rowvar=0)			#计算协方差矩阵
    eigVals,eigVects = linalg.eig(mat(covMat))	#计算协方差矩阵的特征值和特征向量
    eigValInd = argsort(eigVals)            	#排序, 找出特征值大的. 其实就是与其他的变化最不相符
    eigValInd = eigValInd[:-(topNfeat+1):-1]  	#保留最上面的N个特征
    redEigVects = eigVects[:,eigValInd]       	#保留最上面的N个特征向量
    lowDDataMat = meanRemoved * redEigVects		#将数据转换到上述N个特征向量构建的新空间中
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    return lowDDataMat, reconMat				#lowDDataMat是原始数据重构之后的矩阵(蓝色)，reconMat是第一主成分(红色)

# coding:utf-8
# !/usr/bin/env python

'''
Created on Jun 1, 2011

@author: Peter
'''
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
import pca

dataMat = pca.loadDataSet('testSet.txt')
lowDMat, reconMat = pca.pca(dataMat, 1)		#lowDDataMat是原始数据重构之后的矩阵(蓝色)，reconMat是第一主成分(红色)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:,0], dataMat[:,1], marker='^', s=90)
ax.scatter(reconMat[:,0], reconMat[:,1], marker='o', s=50, c='red')
plt.show()

# coding:utf-8
# !/usr/bin/env python

'''
Created on Jun 1, 2011

@author: Peter
'''
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
import pca

n = 1000 #number of points to create
xcord0 = []; ycord0 = []
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
markers =[]
colors =[]
fw = open('testSet3.txt','w')
for i in range(n):			#随机生成1000个二维数据，这1000个二维数据会被标记上0/1/2三个标签
    groupNum = int(3*random.uniform())
    [r0,r1] = random.standard_normal(2)
    if groupNum == 0:
        x = r0 + 16.0
        y = 1.0*r1 + x
        xcord0.append(x)
        ycord0.append(y)
    elif groupNum == 1:
        x = r0 + 8.0
        y = 1.0*r1 + x
        xcord1.append(x)
        ycord1.append(y)
    elif groupNum == 2:
        x = r0 + 0.0
        y = 1.0*r1 + x
        xcord2.append(x)
        ycord2.append(y)
    fw.write("%f\t%f\t%d\n" % (x, y, groupNum))

fw.close()
fig = plt.figure()

ax = fig.add_subplot(211)		#第一幅图
ax.scatter(xcord0,ycord0, marker='^', s=90)
ax.scatter(xcord1,ycord1, marker='o', s=50,  c='red')
ax.scatter(xcord2,ycord2, marker='v', s=50,  c='yellow')

ax = fig.add_subplot(212)		#第二幅图
myDat = pca.loadDataSet('testSet3.txt')
#myDat是(100,3)，降维之后lowDDat是(100,1)
lowDDat,reconDat = pca.pca(myDat[:,0:2],1)	#lowDDat是原始数据重构降维之后的矩阵，reconDat是第一主成分
label0Mat = lowDDat[nonzero(myDat[:,2]==0)[0],:2][0] #get the items with label 0
label1Mat = lowDDat[nonzero(myDat[:,2]==1)[0],:2][0] #get the items with label 1
label2Mat = lowDDat[nonzero(myDat[:,2]==2)[0],:2][0] #get the items with label 2

#ax.scatter(label0Mat[:,0],label0Mat[:,1], marker='^', s=90)
#ax.scatter(label1Mat[:,0],label1Mat[:,1], marker='o', s=50,  c='red')
#ax.scatter(label2Mat[:,0],label2Mat[:,1], marker='v', s=50,  c='yellow')
ax.scatter(label0Mat[:,0].flatten().A[0],zeros(shape(label0Mat)[0]), marker='^', s=90)
ax.scatter(label1Mat[:,0].flatten().A[0],zeros(shape(label1Mat)[0]), marker='o', s=50,  c='red')
ax.scatter(label2Mat[:,0].flatten().A[0],zeros(shape(label2Mat)[0]), marker='v', s=50,  c='yellow')
plt.show()

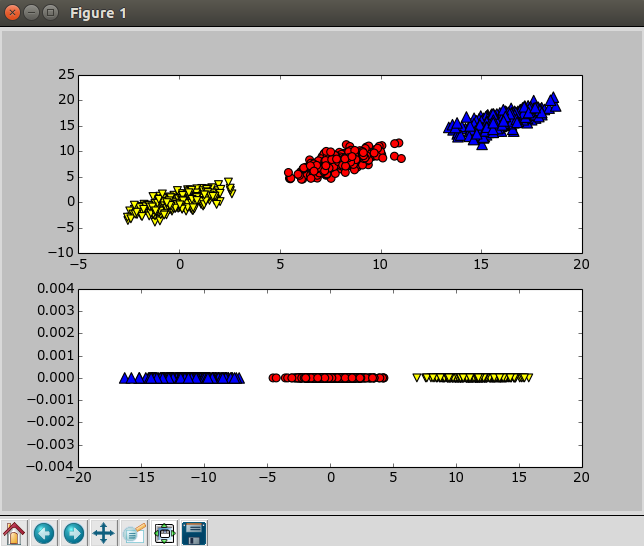
PCA可以从数据中识别其主要特征，它是通过沿着数据最大方差方向旋转坐标轴来实现的。选择方差最大的方向作为第一条坐标轴，后续坐标轴则与前面的坐标轴正交。协方差矩阵上的特征值分析可以用一系列的正交坐标轴来获取。