MySQL Error 1215: Cannot add foreign key constraint

调度器 堆 优先级队列

堆和栈的理解和区别，C语言堆和栈完全攻略 http://c.biancheng.net/c/stack/

数据结构的堆和栈

在数据结构中，栈是一种可以实现“先进后出”（或者称为“后进先出”）的存储结构。假设给定栈 S=（a₀，a₁，…，a_n-1），则称 a₀ 为栈底，a_n-1 为栈顶。进栈则按照 a₀，a₁，…，a_n-1 的顺序进行进栈；而出栈的顺序则需要反过来，按照“后存放的先取，先存放的后取”的原则进行，则 a_n-1 先退出栈，然后 a_n-2 才能够退出，最后再退出 a₀。

在实际编程中，可以通过两种方式来实现：使用数组的形式来实现栈，这种栈也称为静态栈；使用链表的形式来实现栈，这种栈也称为动态栈。

相对于栈的“先进后出”特性，堆则是一种经过排序的树形数据结构，常用来实现优先队列等。假设有一个集合 K={k₀，k₁，…，k_n-1}，把它的所有元素按完全二叉树的顺序存放在一个数组中，并且满足：

Python - DS Introduction - Tutorialspoint https://www.tutorialspoint.com/python_data_structure/python_data_structure_introduction.htm

Liner Data Structures

These are the data structures which store the data elements in a sequential manner.

• Array: It is a sequential arrangement of data elements paired with the index of the data element.
• Linked List: Each data element contains a link to another element along with the data present in it.
• Stack: It is a data structure which follows only to specific order of operation. LIFO(last in First Out) or FILO(First in Last Out).
• Queue: It is similar to Stack but the order of operation is only FIFO(First In First Out).
• Matrix: It is two dimensional data structure in which the data element is referred by a pair of indices.

Non-Liner Data Structures

These are the data structures in which there is no sequential linking of data elements. Any pair or group of data elements can be linked to each other and can be accessed without a strict sequence.

• Binary Tree: It is a data structure where each data element can be connected to maximum two other data elements and it starts with a root node.
• Heap: It is a special case of Tree data structure where the data in the parent node is either strictly greater than/ equal to the child nodes or strictly less than it’s child nodes.
• Hash Table: It is a data structure which is made of arrays associated with each other using a hash function. It retrieves values using keys rather than index from a data element.
• Graph: .It is an arrangement of vertices and nodes where some of the nodes are connected to each other through links.

栈 stack是线性的数据结构

堆 heap是非线性的数据结构

完全二叉树

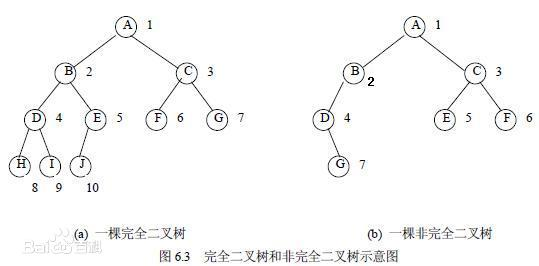
https://baike.baidu.com/item/完全二叉树/7773232

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

 

 

中文名

完全二叉树

外文名

Complete Binary Tree

实    质

效率很高的数据结构

特    点

叶子结点只可能在最大的两层出现

性    质

度为1的点只有1个或0个

应用学科

计算机科学

算法思路

判断一棵树是否是完全二叉树的思路

1>如果树为空，则直接返回错
　　2>如果树不为空：层序遍历二叉树
　　2.1>如果一个结点左右孩子都不为空，则pop该节点，将其左右孩子入队列；
　　2.1>如果遇到一个结点，左孩子为空，右孩子不为空，则该树一定不是完全二叉树；
　　2.2>如果遇到一个结点，左孩子不为空，右孩子为空；或者左右孩子都为空；则该节点之后的队列中的结点都为叶子节点；该树才是完全二叉树，否则就不是完全二叉树；

 

 

class Stack:
    def __init__(self):
        self.stack = []
 
    def add(self, dataval):
        if dataval not in self.stack:
            self.stack.append(dataval)
            return True
        else:
            return False
 
    def peek(self):
        return self.stack[-1]
 
    def remove(self):
        if len(self.stack) <= 0:
            return 'No element in the Stack'
        else:
            return self.stack.pop()
 
AStack = Stack()
AStack.add('Mon')
AStack.peek()
print(AStack.peek())
AStack.add('Wed')
AStack.add('Thu')
print(AStack.peek())
AStack.remove()
 
Python - Stack - Tutorialspoint https://www.tutorialspoint.com/python_data_structure/python_stack.htm
 

 

 

py381\Lib\heapq.py

Python - Heaps - Tutorialspoint https://www.tutorialspoint.com/python_data_structure/python_heaps.htm

大顶堆 小顶堆

二元竞标赛（binary tournament）

"""Heap queue algorithm (a.k.a. priority queue).
 
Heaps are arrays for which a[k] <= a[2*k+1] and a[k] <= a[2*k+2] for
all k, counting elements from 0.  For the sake of comparison,
non-existing elements are considered to be infinite.  The interesting
property of a heap is that a[0] is always its smallest element.
 
Usage:
 
heap = []            # creates an empty heap
heappush(heap, item) # pushes a new item on the heap
item = heappop(heap) # pops the smallest item from the heap
item = heap[0]       # smallest item on the heap without popping it
heapify(x)           # transforms list into a heap, in-place, in linear time
item = heapreplace(heap, item) # pops and returns smallest item, and adds
                               # new item; the heap size is unchanged
 
Our API differs from textbook heap algorithms as follows:
 
- We use 0-based indexing.  This makes the relationship between the
  index for a node and the indexes for its children slightly less
  obvious, but is more suitable since Python uses 0-based indexing.
 
- Our heappop() method returns the smallest item, not the largest.
 
These two make it possible to view the heap as a regular Python list
without surprises: heap[0] is the smallest item, and heap.sort()
maintains the heap invariant!
"""
 
# Original code by Kevin O'Connor, augmented by Tim Peters and Raymond Hettinger
 
__about__ = """Heap queues
 
[explanation by François Pinard]
 
Heaps are arrays for which a[k] <= a[2*k+1] and a[k] <= a[2*k+2] for
all k, counting elements from 0.  For the sake of comparison,
non-existing elements are considered to be infinite.  The interesting
property of a heap is that a[0] is always its smallest element.
 
The strange invariant above is meant to be an efficient memory
representation for a tournament.  The numbers below are `k', not a[k]:
 
                                   0
 
                  1                                 2
 
          3               4                5               6
 
      7       8       9       10      11      12      13      14
 
    15 16   17 18   19 20   21 22   23 24   25 26   27 28   29 30
 
In the tree above, each cell `k' is topping `2*k+1' and `2*k+2'.  In
a usual binary tournament we see in sports, each cell is the winner
over the two cells it tops, and we can trace the winner down the tree
to see all opponents s/he had.  However, in many computer applications
of such tournaments, we do not need to trace the history of a winner.
To be more memory efficient, when a winner is promoted, we try to
replace it by something else at a lower level, and the rule becomes
that a cell and the two cells it tops contain three different items,
but the top cell "wins" over the two topped cells.
 
If this heap invariant is protected at all time, index 0 is clearly
the overall winner.  The simplest algorithmic way to remove it and
find the "next" winner is to move some loser (let's say cell 30 in the
diagram above) into the 0 position, and then percolate this new 0 down
the tree, exchanging values, until the invariant is re-established.
This is clearly logarithmic on the total number of items in the tree.
By iterating over all items, you get an O(n ln n) sort.
 
A nice feature of this sort is that you can efficiently insert new
items while the sort is going on, provided that the inserted items are
not "better" than the last 0'th element you extracted.  This is
especially useful in simulation contexts, where the tree holds all
incoming events, and the "win" condition means the smallest scheduled
time.  When an event schedule other events for execution, they are
scheduled into the future, so they can easily go into the heap.  So, a
heap is a good structure for implementing schedulers (this is what I
used for my MIDI sequencer :-).
 
Various structures for implementing schedulers have been extensively
studied, and heaps are good for this, as they are reasonably speedy,
the speed is almost constant, and the worst case is not much different
than the average case.  However, there are other representations which
are more efficient overall, yet the worst cases might be terrible.
 
Heaps are also very useful in big disk sorts.  You most probably all
know that a big sort implies producing "runs" (which are pre-sorted
sequences, which size is usually related to the amount of CPU memory),
followed by a merging passes for these runs, which merging is often
very cleverly organised[1].  It is very important that the initial
sort produces the longest runs possible.  Tournaments are a good way
to that.  If, using all the memory available to hold a tournament, you
replace and percolate items that happen to fit the current run, you'll
produce runs which are twice the size of the memory for random input,
and much better for input fuzzily ordered.
 
Moreover, if you output the 0'th item on disk and get an input which
may not fit in the current tournament (because the value "wins" over
the last output value), it cannot fit in the heap, so the size of the
heap decreases.  The freed memory could be cleverly reused immediately
for progressively building a second heap, which grows at exactly the
same rate the first heap is melting.  When the first heap completely
vanishes, you switch heaps and start a new run.  Clever and quite
effective!
 
In a word, heaps are useful memory structures to know.  I use them in
a few applications, and I think it is good to keep a `heap' module
around. :-)
 
--------------------
[1] The disk balancing algorithms which are current, nowadays, are
more annoying than clever, and this is a consequence of the seeking
capabilities of the disks.  On devices which cannot seek, like big
tape drives, the story was quite different, and one had to be very
clever to ensure (far in advance) that each tape movement will be the
most effective possible (that is, will best participate at
"progressing" the merge).  Some tapes were even able to read
backwards, and this was also used to avoid the rewinding time.
Believe me, real good tape sorts were quite spectacular to watch!
From all times, sorting has always been a Great Art! :-)
"""
 
数据结构与算法(4)——优先队列和堆 - 我没有三颗心脏 - 博客园 https://www.cnblogs.com/wmyskxz/p/9301021.html

https://baike.baidu.com/item/优先队列/9354754?fr=aladdin

优先队列(priority queue)

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

 

中文名

优先队列

外文名

priority queue

特    点

元素被赋予优先级

类    型

数据结构

定    义

一种先进先出的数据结构，元素在队列尾追加，而从队列头删除

实现方式

通常采用堆数据结构

 

 

 

 

 

 

 

可以将优先级队列想象为已修改的队列，但是当一个人从队列中获取下一个元素时，将首先检索优先级最高的元素。

堆栈和队列可以被建模为特定类型的优先级队列。提醒一下，堆栈和队列的行为方式如下：

堆栈 - 元素以最后一个顺序被拉入（例如，一叠纸）

队列 - 元素先进先出（例如，自助餐厅中的一条线）

在堆栈中，每个插入元素的优先级是单调递增的;因此，插入的最后一个元素始终是第一个检索的元素。在队列中，每个插入元素的优先级是单调递减的;因此，插入的第一个元素始终是第一个检索到的元素

 

有限的元素集合,每个元素都有一个优先权

操作

Create ( ):创建一个空的优先队列

Size ( ):返回队列中的元素数目

Max ( ):返回具有最大优先权的元素

Insert (x):将x插入队列

DeleteMax (x):从队列中删除具有最大优先权的元素,并将该元素返回至x

}

优先队列插入和删除元素的复杂度都是O(log2n)，所以很快。

另一种描述方法是采用有序线性表,当元素按递增次序排列,使用链表时则按递减次序排列,这两种描述方法的删除时间均为( 1 ),插入操作所需时间为(n).

例：

假设我们对机器服务进行收费.每个用户每次使用机器所付费用都是相同的,但每个

用户所需要服务时间都不同.为获得最大利润,假设只要有用户机器就不会空闲,我们可以把

等待使用该机器的用户组织成一个最小优先队列,优先权即为用户所需服务时间.当一个新的

用户需要使用机器时,将他/她的请求加入优先队列.一旦机器可用,则为需要最少服务时间

(即具有最高优先权)的用户提供服务.

如果每个用户所需时间相同,但用户愿意支付的费用不同,则可以用支付费用作为优先权,

一旦机器可用,所交费用最多的用户可最先得到服务,这时就要选择最大优先队列.

 

 

优先队列的应用

• 数据压缩：赫夫曼编码算法；
• 最短路径算法：Dijkstra算法；
• 最小生成树算法：Prim算法；
• 事件驱动仿真：顾客排队算法；
• 选择问题：查找第k个最小元素；
• 等等等等....

heapq — Heap queue algorithm — Python 3.8.2 documentation https://docs.python.org/3.8/library/heapq.html

This module provides an implementation of the heap queue algorithm, also known as the priority queue algorithm.

堆队列 优先级队列