洛谷P2178 品酒大会【后缀数组】【单调栈】

题目描述

一年一度的“幻影阁夏日品酒大会”隆重开幕了。大会包含品尝和趣味挑战两个环节，分别向优胜者颁发“首席品酒家”和“首席猎手”两个奖项，吸引了众多品酒师参加。

在大会的晚餐上，调酒师 Rainbow 调制了 n 杯鸡尾酒。这 n 杯鸡尾酒排成一行，其中第 n 杯酒 (1 ≤ i ≤ n) 被贴上了一个标签si，每个标签都是 26 个小写英文字母之一。设 str(l, r)表示第 l 杯酒到第 r 杯酒的 r − l + 1 个标签顺次连接构成的字符串。若 str(p, po) = str(q, qo)，其中 1 ≤ p ≤ po ≤ n, 1 ≤ q ≤ qo ≤ n, p ≠ q, po − p + 1 = qo − q + 1 = r ，则称第 p 杯酒与第 q 杯酒是“ r 相似” 的。当然两杯“ r 相似”(r > 1)的酒同时也是“ 1 相似”、“ 2 相似”、……、“ (r − 1) 相似”的。特别地，对于任意的 1 ≤ p , q ≤ n ， p ≠ q ，第 p 杯酒和第 q 杯酒都是“ 0 相似”的。

在品尝环节上，品酒师 Freda 轻松地评定了每一杯酒的美味度，凭借其专业的水准和经验成功夺取了“首席品酒家”的称号，其中第 i 杯酒 (1 ≤ i ≤ n) 的美味度为 ai 。现在 Rainbow 公布了挑战环节的问题：本次大会调制的鸡尾酒有一个特点，如果把第 p 杯酒与第 q 杯酒调兑在一起，将得到一杯美味度为 ap*aq 的酒。现在请各位品酒师分别对于 r = 0,1,2, ⋯ , n − 1 ，统计出有多少种方法可以选出 2 杯“ r 相似”的酒，并回答选择 2 杯“ r 相似”的酒调兑可以得到的美味度的最大值。

输入输出格式

输入格式：

第 1 行包含 1 个正整数 n ，表示鸡尾酒的杯数。

第 2 行包含一个长度为 n 的字符串 S，其中第 i 个字符表示第 i 杯酒的标签。

第 3 行包含 n 个整数，相邻整数之间用单个空格隔开，其中第 i 个整数表示第 i 杯酒的美味度 ai 。

输出格式：

包括 n 行。第 i 行输出 2 个整数，中间用单个空格隔开。第 1 个整数表示选出两杯“ (i − 1) 相似”的酒的方案数，第 2 个整数表示选出两杯 “ (i − 1) 相似”的酒调兑可以得到的最大美味度。若不存在两杯“ (i − 1) 相似” 的酒，这两个数均为 0 。

输入输出样例

输入样例#1：复制

10
ponoiiipoi
2 1 4 7 4 8 3 6 4 7

输出样例#1：复制

输入样例#2：复制

12
abaabaabaaba
1 -2 3 -4 5 -6 7 -8 9 -10 11 -12

输出样例#2：复制

说明

【样例说明 1】

用二元组 (p, q) 表示第 p 杯酒与第 q 杯酒。

0 相似：所有 45 对二元组都是 0 相似的，美味度最大的是 8 × 7 = 56 。

1 相似： (1,8) (2,4) (2,9) (4,9) (5,6) (5,7) (5,10) (6,7) (6,10) (7,10) ，最大的 8 × 7 = 56 。

2 相似： (1,8) (4,9) (5,6) ，最大的 4 × 8 = 32 。

没有 3,4,5, ⋯ ,9 相似的两杯酒，故均输出 0 。

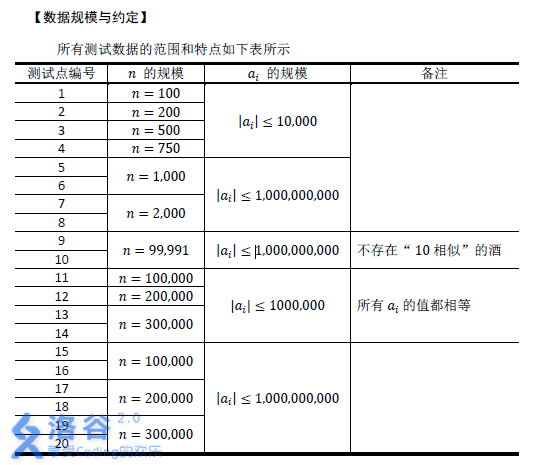
【时限1s，内存512M】

思路：

给定一个字符串，要求分别找出公共子串长度为0~n-1的串的数目。并且每个酒有一个值，求这些方案中哪两个值之积最大。

题意：

因为有负值，所以要同时维护最大值和最小值，负负得正。

一直70分，后来把best的初始化从-inf改成了LLONG_MIN就过了。

因为题目中r相似一定是r-1,r-2...相似的。所以处理一下严格r相似的，然后累加一下就好了。

题解好多都是用的并查集。单调栈其实也是一个道理。栈里存的就是这个区间。

碰到了height更小的时候就应该出栈了。每次就是把产生了贡献的区间并起来。

 #include <iostream>
 #include <set>
 #include <cmath>
 #include <stdio.h>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <map>
 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 #define inf 0x7f7f7f7f
 
 const int maxn = 3e5 + ;
 
 char str[maxn];
 int n, s[maxn];
 LL val[maxn];
 int sa[maxn];
 int t1[maxn], t2[maxn], c[maxn];
 int rnk[maxn], height[maxn];
 LL cnt[maxn], best[maxn];
 int top, sta[maxn], mx[maxn], mi[maxn], sz[maxn];
 
 void build_sa(int s[], int n, int m)
 {
     int i, j, p, *x = t1, *y = t2;
     for(i = ; i < m; i++)c[i] = ;
     for(i = ; i < n; i++)c[x[i] = s[i]]++;
     for(i = ; i < m; i++)c[i] += c[i - ];
     for(i = n - ; i >= ; i--)sa[--c[x[i]]] = i;
     for(j = ; j <= n; j <<= ){
         p = ;
         for(i = n - j; i < n; i++)y[p++] = i;
         for(i = ; i < n; i++)if(sa[i] >= j)y[p++] = sa[i] - j;
         for(i = ; i < m; i++)c[i] = ;
         for(i = ; i < n; i++)c[x[y[i]]]++;
         for(i = ; i < m; i++)c[i] += c[i - ];
         for(i = n - ; i >= ; i--)sa[--c[x[y[i]]]] = y[i];
         swap(x, y);
         p = ;
         x[sa[]] = ;
         for(i = ; i < n; i++)
             x[sa[i]] = y[sa[i - ]] == y[sa[i]] && y[sa[i - ] + j] == y[sa[i] + j] ? p - : p++;
         if(p >= n)break;
         m = p;
     }
 }
 
 void get_height(int s[], int n)
 {
     int i, j, k = ;
     for(i = ; i <= n; i++){
         rnk[sa[i]] = i;
     }
     for(i = ; i <= n; i++){
         if(k)k--;
         j = sa[rnk[i] - ];
         while(s[i + k] == s[j + k])k++;
         height[rnk[i]] = k;
     }
 }
 
 void work()
 {
     int ksz, kmx, kmi;
     for(int i = ; i <= n; i++){
         ksz = ;
         kmx = kmi = val[sa[i - ]];
         while(top && sta[top] >= height[i]){
             cnt[sta[top]] += 1LL * sz[top] * ksz;
             best[sta[top]] = max(best[sta[top]], max(1LL * mx[top] * kmx, 1LL * mi[top] * kmi));
             ksz += sz[top];
             kmx = max(kmx, mx[top]);
             kmi = min(kmi, mi[top]);
             --top;
         }
         ++top;
         sta[top] = height[i];
         sz[top] = ksz;
         mi[top] = kmi;
         mx[top] = kmx;
     }
     ksz = ;
     kmx = kmi = val[sa[n]];
     for(int i = top; i >= ; i--){
         cnt[sta[i]] += 1LL * sz[i] * ksz;
         best[sta[i]] = max(best[sta[i]], max(1LL * mx[i] * kmx, 1LL * mi[i] * kmi));
         ksz += sz[i];
         kmx = max(kmx, mx[i]);
         kmi = min(kmi, mi[i]);
     }
 }
 
 int main()
 {
     scanf("%d", &n);
     scanf("%s", str + );
     best[] = LLONG_MIN;
     //cout<<best[0]<<endl;
     //cout<<-inf<<endl;
     for(int i = ; i <= n; i++){
         scanf("%lld", &val[i]);
         s[i] = str[i];
         cnt[i] = ;
         best[i] = LLONG_MIN;
     }
     build_sa(s, n + , );
     /*for(int i = 0; i <= n + 1; i++){
         cout<<sa[i]<<endl;
     }*/
     get_height(s, n);
     work();
     for(int i = n - ; i >= ; i--){
         cnt[i] += cnt[i + ];
         best[i] = max(best[i], best[i + ]);
     }
     for(int i = ; i < n; i++){
         if(!cnt[i])best[i] = ;
         printf("%lld %lld\n", cnt[i], best[i]);
     }
 
     return ;
 }