[hihoCoder] 第四十八周: 拓扑排序·二

题目1 : 拓扑排序·二

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi和小Ho所在学校的校园网被黑客入侵并投放了病毒。这事在校内BBS上立刻引起了大家的讨论，当然小Hi和小Ho也参与到了其中。从大家各自了解的情况中，小Hi和小Ho整理得到了以下的信息：

• 校园网主干是由N个节点(编号1..N)组成，这些节点之间有一些单向的网路连接。若存在一条网路连接(u,v)链接了节点u和节点v，则节点u可以向节点v发送信息，但是节点v不能通过该链接向节点u发送信息。
• 在刚感染病毒时，校园网立刻切断了一些网络链接，恰好使得剩下网络连接不存在环，避免了节点被反复感染。也就是说从节点i扩散出的病毒，一定不会再回到节点i。
• 当1个病毒感染了节点后，它并不会检查这个节点是否被感染，而是直接将自身的拷贝向所有邻居节点发送，它自身则会留在当前节点。所以一个节点有可能存在多个病毒。
• 现在已经知道黑客在一开始在K个节点上分别投放了一个病毒。

举个例子，假设切断部分网络连接后学校网络如下图所示，由4个节点和4条链接构成。最开始只有节点1上有病毒。

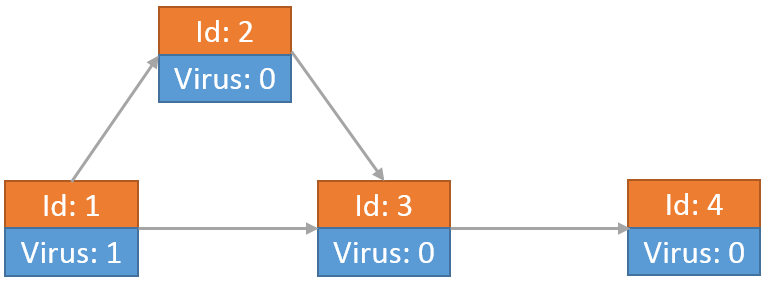
最开始节点1向节点2和节点3传送了病毒，自身留有1个病毒：

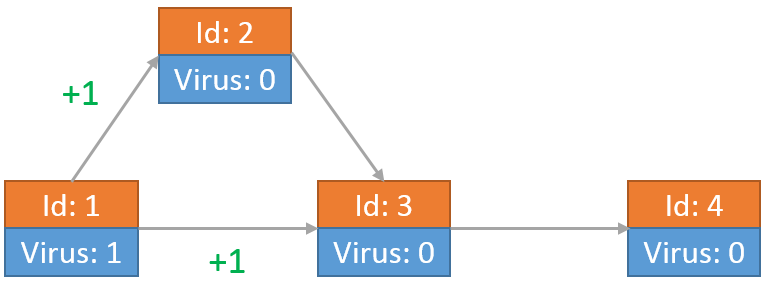
其中一个病毒到达节点2后，向节点3传送了一个病毒。另一个到达节点3的病毒向节点4发送自己的拷贝：

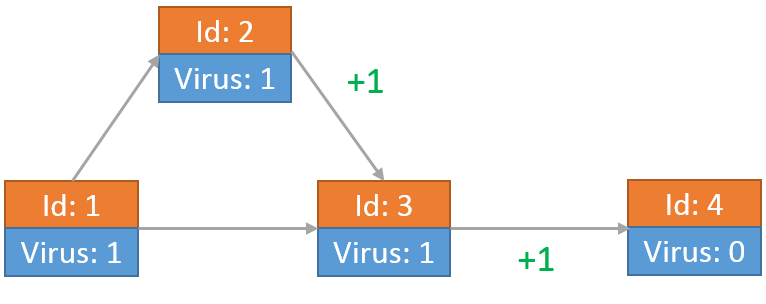
当从节点2传送到节点3的病毒到达之后，该病毒又发送了一份自己的拷贝向节点4。此时节点3上留有2个病毒：

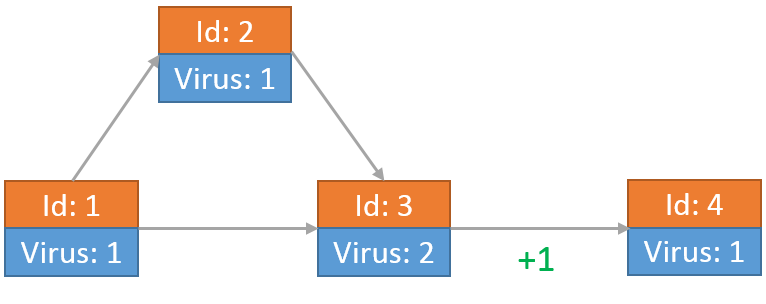
最后每个节点上的病毒为：

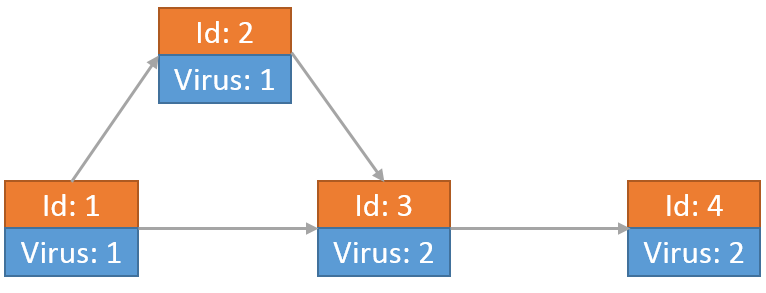
小Hi和小Ho根据目前的情况发现一段时间之后，所有的节点病毒数量一定不会再发生变化。那么对于整个网络来说，最后会有多少个病毒呢？

提示：拓扑排序的应用

输入

第1行：3个整数N,M,K，1≤K≤N≤100,000，1≤M≤500,000

第2行：K个整数A[i]，A[i]表示黑客在节点A[i]上放了1个病毒。1≤A[i]≤N

第3..M+2行：每行2个整数 u,v，表示存在一条从节点u到节点v的网络链接。数据保证为无环图。1≤u,v≤N

输出

第1行：1个整数，表示最后整个网络的病毒数量 MOD 142857

样例输入

4 4 1
1
1 2
1 3
2 3
3 4

样例输出

6

 #include <bits/stdc++.h>
 using namespace std;

 #define MOD 142857

 int N, M, K;
 vector<vector<int>> graph;
 vector<int> inDegree;
 vector<int> virus;
 int m, u, v;

 void solve() {
     int res = ;
     queue<int> que;
     for (int i = ; i <= N; ++i) if (inDegree[i] == ) que.push(i);
     while (!que.empty()) {
         int u = que.front();
         que.pop();
         for (int v : graph[u]) {
             virus[v] += virus[u];
             virus[v] %= MOD;
             --inDegree[v];
             if (inDegree[v] == ) que.push(v);
         }
     }
     for (int v : virus) {
         res += v;
         res %= MOD;
     }
     cout << res << endl;
 }

 int main() {
     while (cin >> N >> M >> K) {
         graph.assign(N + , vector<int>());
         virus.assign(N + , );
         inDegree.assign(N + , );
         for (int i = ; i < K; ++i) {
             cin >> m;
             virus[m] = ;
         }
         for (int i = ; i < M; ++i) {
             cin >> u >> v;
             graph[u].push_back(v);
             ++inDegree[v];
         }
         solve();
     }
     return ;
 }