决策树之Cart算法一

Contents

   1. CART算法的认识

   2. CART算法的原理

   3. CART算法的实现

1. CART算法的认识

Classification And Regression Tree，即分类回归树算法，简称CART算法，它是决策树的一种实现，通

常决策树主要有三种实现，分别是ID3算法，CART算法和C4.5算法。

CART算法是一种二分递归分割技术，把当前样本划分为两个子样本，使得生成的每个非叶子结点都有两个分支，

因此CART算法生成的决策树是结构简洁的二叉树。由于CART算法构成的是一个二叉树，它在每一步的决策时只能

是“是”或者“否”，即使一个feature有多个取值，也是把数据分为两部分。在CART算法中主要分为两个步骤

（1）将样本递归划分进行建树过程

（2）用验证数据进行剪枝

2. CART算法的原理

上面说到了CART算法分为两个过程，其中第一个过程进行递归建立二叉树，那么它是如何进行划分的 ？

设代表单个样本的个属性，表示所属类别。CART算法通过递归的方式将维的空间划分为不重

叠的矩形。划分步骤大致如下

（1）选一个自变量，再选取的一个值，把维空间划分为两部分，一部分的所有点都满足，

另一部分的所有点都满足，对非连续变量来说属性值的取值只有两个，即等于该值或不等于该值。

（2）递归处理，将上面得到的两部分按步骤（1）重新选取一个属性继续划分，直到把整个维空间都划分完。

在划分时候有一个问题，它是按照什么标准来划分的 ？ 对于一个变量属性来说，它的划分点是一对连续变量属

性值的中点。假设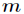个样本的集合一个属性有个连续的值，那么则会有个分裂点，每个分裂点为相邻

两个连续值的均值。每个属性的划分按照能减少的杂质的量来进行排序，而杂质的减少量定义为划分前的杂质减

去划分后的每个节点的杂质量划分所占比率之和。而杂质度量方法常用Gini指标，假设一个样本共有类，那么

一个节点的Gini不纯度可定义为

其中表示属于类的概率，当Gini(A)=0时，所有样本属于同类，所有类在节点中以等概率出现时，Gini(A)

最大化，此时。

有了上述理论基础，实际的递归划分过程是这样的：如果当前节点的所有样本都不属于同一类或者只剩下一个样

本，那么此节点为非叶子节点，所以会尝试样本的每个属性以及每个属性对应的分裂点，尝试找到杂质变量最大

的一个划分，该属性划分的子树即为最优分支。

下面举个简单的例子，如下图

在上述图中，属性有3个，分别是有房情况，婚姻状况和年收入，其中有房情况和婚姻状况是离散的取值，而年

收入是连续的取值。拖欠贷款者属于分类的结果。

假设现在来看有房情况这个属性，那么按照它划分后的Gini指数计算如下

而对于婚姻状况属性来说，它的取值有3种，按照每种属性值分裂后Gini指标计算如下

最后还有一个取值连续的属性，年收入，它的取值是连续的，那么连续的取值采用分裂点进行分裂。如下

根据这样的分裂规则CART算法就能完成建树过程。

建树完成后就进行第二步了，即根据验证数据进行剪枝。在CART树的建树过程中，可能存在Overfitting，许多

分支中反映的是数据中的异常，这样的决策树对分类的准确性不高，那么需要检测并减去这些不可靠的分支。决策

树常用的剪枝有事前剪枝和事后剪枝，CART算法采用事后剪枝，具体方法为代价复杂性剪枝法。可参考如下链接

剪枝参考：http://www.cnblogs.com/zhangchaoyang/articles/2709922.html

3. CART算法的实现

以下代码是网上找的CART算法的MATLAB实现。

CART  

function D = CART(train_features, train_targets, params, region)  

% Classify using classification and regression trees
% Inputs:
% features - Train features
% targets     - Train targets
% params - [Impurity type, Percentage of incorrectly assigned samples at a node]
%                   Impurity can be: Entropy, Variance (or Gini), or Missclassification
% region     - Decision region vector: [-x x -y y number_of_points]
%
% Outputs
% D - Decision sufrace  

[Ni, M]    = size(train_features);  

%Get parameters
[split_type, inc_node] = process_params(params);  

%For the decision region
N           = region(5);
mx          = ones(N,1) * linspace (region(1),region(2),N);
my          = linspace (region(3),region(4),N)' * ones(1,N);
flatxy      = [mx(:), my(:)]';  

%Preprocessing
[f, t, UW, m]   = PCA(train_features, train_targets, Ni, region);
train_features  = UW * (train_features - m*ones(1,M));;
flatxy          = UW * (flatxy - m*ones(1,N^2));;  

%Build the tree recursively
disp('Building tree')
tree        = make_tree(train_features, train_targets, M, split_type, inc_node, region);  

%Make the decision region according to the tree
disp('Building decision surface using the tree')
targets = use_tree(flatxy, 1:N^2, tree);  

D = reshape(targets,N,N);
%END  

function targets = use_tree(features, indices, tree)
%Classify recursively using a tree  

if isnumeric(tree.Raction)
   %Reached an end node
   targets = zeros(1,size(features,2));
   targets(indices) = tree.Raction(1);
else
   %Reached a branching, so:
   %Find who goes where
   in_right    = indices(find(eval(tree.Raction)));
   in_left     = indices(find(eval(tree.Laction)));  

   Ltargets = use_tree(features, in_left, tree.left);
   Rtargets = use_tree(features, in_right, tree.right);  

   targets = Ltargets + Rtargets;
end
%END use_tree  

function tree = make_tree(features, targets, Dlength, split_type, inc_node, region)
%Build a tree recursively  

if (length(unique(targets)) == 1),
   %There is only one type of targets, and this generates a warning, so deal with it separately
   tree.right      = [];
   tree.left       = [];
   tree.Raction    = targets(1);
   tree.Laction    = targets(1);
   break
end  

[Ni, M] = size(features);
Nt      = unique(targets);
N       = hist(targets, Nt);  

if ((sum(N < Dlength*inc_node) == length(Nt) - 1) | (M == 1)),
   %No further splitting is neccessary
   tree.right      = [];
   tree.left       = [];
   if (length(Nt) ~= 1),
      MLlabel   = find(N == max(N));
   else
      MLlabel   = 1;
   end
   tree.Raction    = Nt(MLlabel);
   tree.Laction    = Nt(MLlabel);  

else
   %Split the node according to the splitting criterion
   deltaI = zeros(1,Ni);
   split_point = zeros(1,Ni);
   op = optimset('Display', 'off');
   for i = 1:Ni,
      split_point(i) = fminbnd('CARTfunctions', region(i*2-1), region(i*2), op, features, targets, i, split_type);
      I(i) = feval('CARTfunctions', split_point(i), features, targets, i, split_type);
   end  

   [m, dim] = min(I);
   loc = split_point(dim);  

   %So, the split is to be on dimention 'dim' at location 'loc'
   indices = 1:M;
   tree.Raction= ['features(' num2str(dim) ',indices) >  ' num2str(loc)];
   tree.Laction= ['features(' num2str(dim) ',indices) <= ' num2str(loc)];
   in_right    = find(eval(tree.Raction));
   in_left     = find(eval(tree.Laction));  

   if isempty(in_right) | isempty(in_left)
      %No possible split found
   tree.right      = [];
   tree.left       = [];
   if (length(Nt) ~= 1),
      MLlabel   = find(N == max(N));
   else
      MLlabel = 1;
   end
   tree.Raction    = Nt(MLlabel);
   tree.Laction    = Nt(MLlabel);
   else
   %...It's possible to build new nodes
   tree.right = make_tree(features(:,in_right), targets(in_right), Dlength, split_type, inc_node, region);
   tree.left  = make_tree(features(:,in_left), targets(in_left), Dlength, split_type, inc_node, region);
   end  

end  

在Julia中的决策树包：https://github.com/bensadeghi/DecisionTree.jl/blob/master/README.md