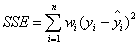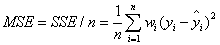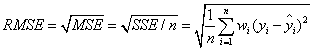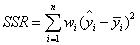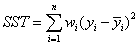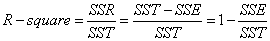SSE(和方差、误差平方和)：The sum of squares due to error
MSE(均方差、方差)：Mean squared error
RMSE(均方根、标准差)：Root mean squared error
R-square(确定系数)：Coefficient of determination
Adjusted R-square：Degree-of-freedom adjusted coefficient of determination

下面我对以上几个名词进行详细的解释下，相信能给大家带来一定的帮助！！

一、SSE(和方差)

该统计参数计算的是拟合数据和原始数据对应点的误差的平方和，计算公式如下

SSE越接近于0，说明模型选择和拟合更好，数据预测也越成功。接下来的MSE和RMSE因为和SSE是同出一宗，所以效果一样

二、MSE(均方差)
该统计参数是预测数据和原始数据对应点误差的平方和的均值，也就是SSE/n，和SSE没有太大的区别，计算公式如下

三、RMSE(均方根)
该统计参数，也叫回归系统的拟合标准差，是MSE的平方根，就算公式如下

在这之前，我们所有的误差参数都是基于预测值(y_hat)和原始值(y)之间的误差(即点对点)。从下面开始是所有的误差都是相对原始数据平均值(y_ba)而展开的(即点对全)!!!

四、R-square(确定系数)
在讲确定系数之前，我们需要介绍另外两个参数SSR和SST，因为确定系数就是由它们两个决定的
(1)SSR：Sum of squares of the regression，即预测数据与原始数据均值之差的平方和，公式如下

(2)SST：Total sum of squares，即原始数据和均值之差的平方和，公式如下

细心的网友会发现，SST=SSE+SSR，呵呵只是一个有趣的问题。而我们的“确定系数”是定义为SSR和SST的比值，故

其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好

SSE,MSE,RMSE,R-square指标讲解的更多相关文章

  1. SSE,MSE,RMSE,R-square 指标讲解

    SSE(和方差.误差平方和):The sum of squares due to error MSE(均方差.方差):Mean squared errorRMSE(均方根.标准差):Root mean ...

  2. Data Mining： SSE,MSE,RMSE,R-square指标讲解

    转载自:http://blog.csdn.net/l18930738887/article/details/50629409 SSE(和方差.误差平方和):The sum of squares due ...

  3. 衡量线性回归法的指标MSE, RMSE,MAE和R Square

    衡量线性回归法的指标:MSE, RMSE和MAE 举个栗子: 对于简单线性回归,目标是找到a,b 使得尽可能小 其实相当于是对训练数据集而言的,即 当我们找到a,b后,对于测试数据集而言 ,理所当然, ...

  4. 【笔记】衡量线性回归法的指标 MSE,RMS,MAE以及评价回归算法 R Square

    衡量线性回归法的指标 MSE,RMS,MAE以及评价回归算法 R Square 衡量线性回归法的指标 对于分类问题来说,我们将原始数据分成了训练数据集和测试数据集两部分,我们使用训练数据集得到模型以后 ...

  5. 线性回归中常见的一些统计学术语（RSE RSS TSS ESS MSE RMSE R2 Pearson's r）

    TSS: Total Sum of Squares(总离差平方和) --- 因变量的方差 RSS: Residual Sum of Squares (残差平方和) ---  由误差导致的真实值和估计值 ...

  6. MSE,RMSE

    MSE: Mean Squared Error 均方误差是指参数估计值与参数真值之差平方的期望值; MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度. RMSE  ...

  7. 回归评价指标MSE、RMSE、MAE、R-Squared

    分类问题的评价指标是准确率,那么回归算法的评价指标就是MSE,RMSE,MAE.R-Squared. MSE和MAE适用于误差相对明显的时候,大的误差也有比较高的权重,RMSE则是针对误差不是很明显的 ...

  8. 机器学习|线性回归三大评价指标实现『MAE, MSE, MAPE』（Python语言描述）

    原文地址 ?传送门 对于回归预测结果,通常会有平均绝对误差.平均绝对百分比误差.均方误差等多个指标进行评价.这里,我们先介绍最常用的3个: 平均绝对误差(MAE) 就是绝对误差的平均值,它的计算公式如 ...

  9. SSE技术详解：一种全新的HTML5服务器推送事件技术

    前言 一般来说,Web端即时通讯技术因受限于浏览器的设计限制,一直以来实现起来并不容易,主流的Web端即时通讯方案大致有4种:传统Ajax短轮询.Comet技术.WebSocket技术.SSE(Ser ...

随机推荐

  1. 吴恩达-coursera-机器学习-week3

    六.逻辑回归(Logistic Regression) 6.1 分类问题 6.2 假说表示 6.3 判定边界 6.4 代价函数 6.5 简化的成本函数和梯度下降 6.6 高级优化 6.7 多类别分类: ...

  2. WEB应用从服务器主动推送Data到客户端有那些方式？

    1)  html5 websocket 2)  WebSocket 通过 Flash 3)  XHR长时间连接 4)  XHR Multipart Streaming 5)  不可见的Iframe 6 ...

  3. PHP 图像居中裁剪函数

    图像居中裁减的大致思路: 1.首先将图像进行缩放,使得缩放后的图像能够恰好覆盖裁减区域.(imagecopyresampled — 重采样拷贝部分图像并调整大小) 2.将缩放后的图像放置在裁减区域中间 ...

  4. ORA-01591 锁定已被有问题的分配事务处理--解决方法(转)

    转载自love wife & love life —Roger 的Oracle技术博客 本文链接地址: ORA-01591: lock held by in-doubt distributed ...

  5. ip定位

    http://www.cnblogs.com/pengcc/p/5294836.html https://wx.jdcloud.com/shop/shopDetail/RTBAsia,里面有各种IP地 ...

  6. CentOS 7设置KVM硬盘模式为SCSI

    找到一下节点,把target节点的dev改成s开头,bus改成scsi即可,并删除address节点: 以此内推,如果要修改为ide需要修改dev为h开头,bus改成ide. 参考: https:// ...

  7. 使用CefSharp在.Net程序中嵌入Chrome浏览器（五）——Javascript交互

    要在CEF中和网页的JS进行交互,首先我们要通过设置启用Javascrit集成功能. CefSharpSettings.LegacyJavascriptBindingEnabled = true; 调 ...

  8. Golang 处理 Json（一）：编码

    JSON 是一种数据格式描述语言.以 key 和 value 构成的哈系结构,类似 Javascript 中的对象,python 中的字典.通常 json 格式的 key 是字符串,其值可以是任意类型 ...

  9. 为什么我不再用 .NET 框架

    .NET平台很棒.真的很棒.直到它不再那么棒.我为什么不再用.NET?简单来说,它限制了我们选择的能力(对我来说很重要),转移了我们的注意力,使得我们向内认知它的安全性,替代了帮助我们认知外面广阔世界 ...

  10. Delphi XE中String、ANSIString、TBytes之间的转换

    一.string转为ansistring1.直接赋值 (有警告)2.ansistring()类型强制转换.(无警告) 二.ansistring 转为string 1.直接赋值 (有警告)2.strin ...