[板子]SPFA算法+链式前向星实现最短路及负权最短路

参考：https://blog.csdn.net/xunalove/article/details/70045815

有关SPFA的介绍就掠过了吧，不是很赞同一些博主说是国内某人最先提出来，Bellman算法论文后面提及过队列优化的问题。

另外，不建议在没有负边权的情况下使用SPFA算法，某些水（sang）平（xin）很（bing）高（kuang）的出题人可能会出卡SPFA的常数- -

所以，在题目没有提及说有负边权的情况下，请使用堆优化的dijkstra。

下面用图说一下SPFA的运行：

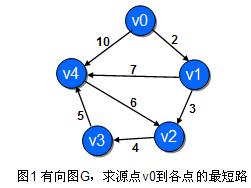
#include<bits/stdc++.h>
const long long inf=2147483647;
const int maxn=10005;
const int maxm=500005;
using namespace std;
int n,m,s,num_edge=0;
int dis[maxn],vis[maxn],head[maxm],outqueue[maxm];//head表示边的序号，指的是当前以x为起点所最后引出的一条边。
struct Edge
{
  int next,to,dis;
}edge[maxm];
void addedge(int from,int to,int dis)
{ //倒着遍历
  edge[++num_edge].next=head[from]; //存储下一条出边
  edge[num_edge].to=to; 
  edge[num_edge].dis=dis; //权值
  head[from]=num_edge; //记录下一次的出边情况
}
bool spfa()
{
  queue<int> q;
 
  for(int i=1; i<=n; i++)
  {
    dis[i]=inf; //初始化
    vis[i]=0;
  }
 
  q.push(s); dis[s]=0; vis[s]=1; //第一个顶点入队，进行标记
  while(!q.empty())
  {
    int u=q.front(); //取出队首
    q.pop(); vis[u]=0; //出队标记
    
   outqueue[u]++;
  if(outqueue[u]>n) return 0;//判断是否有负边权
   
    for(int i=head[u];i!=0;i=edge[i].next)//找这条边的同起点的上一条边
    {
      int v=edge[i].to;
      if(dis[v]>dis[u]+edge[i].dis) //如果有最短路就更改
      {
        dis[v]=dis[u]+edge[i].dis;
        if(vis[v]==0) //未入队则入队
        {
          vis[v]=1; //标记入队
          q.push(v);
        }
      }
    }
  }
  return 1;
}
int main()
{
  cin>>n>>m>>s;
  for(int i=1; i<=m; i++)
  {
    int f,g,w;
    cin>>f>>g>>w;
    addedge(f,g,w);//无向边中结构体数组要开到边数的两倍
  }
  spfa();
  for(int i=1; i<=n; i++)
    if(s==i) cout<<0<<" ";
      else cout<<dis[i]<<" ";
  return 0;
}

head[x]是边的序号，指的是当前以x为起点所最后引出的一条边。