acm数论之旅--组合数（转载）

随笔 - 20  文章 - 0  评论 - 73

ACM数论之旅8---组合数（组合大法好(,,• ₃ •,,) ）

 补充：全错排公式：https://blog.csdn.net/Carey_Lu/article/details/49742129

https://blog.csdn.net/u011345136/article/details/38778121

一道组合数与全错排的公式。

组合数并不陌生(´・ω・`)

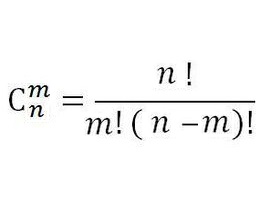
我们都学过组合数

会求组合数吗

一般我们用杨辉三角性质

杨辉三角上的每一个数字都等于它的左上方和右上方的和（除了边界）

第n行，第m个就是，就是C(n, m) （从0开始）

电脑上我们就开一个数组保存，像这样

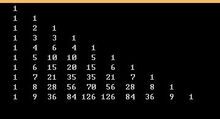
用递推求

 1 #include<cstdio>
 2 const int N = 2000 + 5;
 3 const int MOD = (int)1e9 + 7;
 4 int comb[N][N];//comb[n][m]就是C(n,m)
 5 void init(){
 6     for(int i = 0; i < N; i ++){
 7         comb[i][0] = comb[i][i] = 1;
 8         for(int j = 1; j < i; j ++){
 9             comb[i][j] = comb[i-1][j] + comb[i-1][j-1];
10             comb[i][j] %= MOD;
11         }
12     }
13 }
14 int main(){
15     init();
16 }

https://ac.nowcoder.com/acm/contest/881#question E题，另外一种求组合数。

#include<bits/stdc++.h>
#define ll long long
#define M (ll)(1e9+7)
using namespace std;
ll CM[]={};
ll Pow(ll a,ll b){  //快速幂
    a%=M;
    ll ans = ;
    for(;b;b>>=)
    {
        if(b&) ans = (ans*a)%M;
        a = (a*a)%M;
    }
    return ans;
}
ll Quk(ll a,ll b){ //快速乘
    a%=M;
    ll ans = ;
    for(;b;b>>=)
    {
        if(b&) ans = (ans+a)%M;
        a = (a+a)%M;
    }
    return ans;
}
ll C(ll m,ll n){ //n>=m
    return Quk(Quk(CM[n],Pow(CM[n-m],M-)),Pow(CM[m],M-))%M;
}
ll A(ll m,ll n){ //n>=m
    return Quk(CM[n],Pow(CM[n-m],M-))%M;
}
int main()
{
    ll a,b;
    for(int i=;i<;i++) CM[i]=Quk(CM[i-],i);
    while(cin>>a>>b)
    {
        ll ans=C(a+b,*(a+b));
        if(a) ans-=C(a-,*(a+b));
        if(b) ans-=C(b-,*(a+b));
        cout<<(ans+*M)%M<<endl;
    }
    return ;
}

需要mod是质数

#include<bits/stdc++.h>
using namespace std;
#define INF 0x3fffffff
#define maxn 100005
typedef long long ll;
ll n,m,k,t;
const ll mod = 1e9+;
ll fac[maxn];
ll inv[maxn];
ll qpow(ll a, ll b)
{
    ll r = , t = a;
    while (b) {
        if (b & )r = (r*t) % mod;
        b >>= ;t = (t*t) % mod;
    }
    return r;
}
void init()
{
    fac[] = ;
    for (int i = ;i <= mmax;i++) fac[i] = fac[i - ] * 1ll * i%mod;
    inv[mmax] = qpow(fac[mmax], mod - );
    for (int i = mmax - ;~i;i--) inv[i] = inv[i + ] * 1ll * (i + ) % mod;
}
ll C(ll n, ll m)
{
    if (m>n) return ;
    if (m == n || m == ) return ;
    return fac[n] * 1ll * inv[n - m] % mod*inv[m] % mod;
}
int main(){
    init();
    while(~scanf("%lld%lld",&n,&m))
        printf("%lld\n",(C(*m+*n,n+m)+mod-(C(*m+*n,n-)+C(*m+*n,m-))%mod)%mod);
}

（PS：大部分题目都要求求余，而且大部分都是对1e9+7这个数求余）

这种方法的复杂度是O(n^2)，有没有O(n)的做法，当然有(´・ω・`)

因为大部分题都有求余，所以我们大可利用逆元的原理（没求余的题目，其实你也可以把MOD自己开的大一点，这样一样可以用逆元做）

根据这个公式

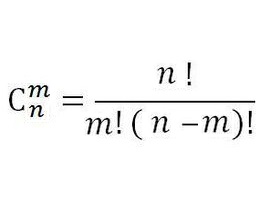
我们需要求阶乘和逆元阶乘

我们就用1e9+7来求余吧

long long F[];
void init(long long p)
{
    F[] = ;
    for(int i = ;i <= p;i++)
        F[i] = F[i-]*i % ();
}
long long inv(long long a,long long m)
{
    if(a == )return ;
    return inv(m%a,m)*(m-m/a)%m;
}
long long Lucas(long long n,long long m,long long p)
{
    long long ans = ;
    while(n&&m)
    {
        long long a = n%p;
        long long b = m%p;
        if(a < b)return ;
        ans = ans*F[a]%p*inv(F[b]*F[a-b]%p,p)%p;
        n /= p;
        m /= p;
    }
    return ans;
}

代码如下：

 1 #include<cstdio>
 2 const int N = 200000 + 5;
 3 const int MOD = (int)1e9 + 7;
 4 int F[N], Finv[N], inv[N];//F是阶乘，Finv是逆元的阶乘
 5 void init(){
 6     inv[1] = 1;
 7     for(int i = 2; i < N; i ++){
 8         inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
 9     }
10     F[0] = Finv[0] = 1;
11     for(int i = 1; i < N; i ++){
12         F[i] = F[i-1] * 1ll * i % MOD;
13         Finv[i] = Finv[i-1] * 1ll * inv[i] % MOD;
14     }
15 }
16 int comb(int n, int m){//comb(n, m)就是C(n, m)
17     if(m < 0 || m > n) return 0;
18     return F[n] * 1ll * Finv[n - m] % MOD * Finv[m] % MOD;
19 }
20 int main(){
21     init();
22 }