快速傅里叶变换（FFT）学习

首先，在写这篇博客之前，我还没有完全学会FFT。

先把会的部分打好，加深一下记忆（也可以说是做笔记吧）。

初三了，还不会FFT，要退役喽……

---

多项式乘法

点开这篇博客之前，你就应该知道，FFT是用来求多项式乘法的。

什么是多项式，什么是多项式乘法？

不讲。初一内容。

如果要求多项式乘法，有一个非常显然的做法，就是暴力。

时间复杂度是O(N2)O(N^2)O(N2)的，很朴素。

然而FFT这个东西可以将其复杂度优化到O(Nlg⁡N)O(N\lg N)O(NlgN)。

---

点值表示法

对s于一个多项式A(x)A(x)A(x)，最朴素的表示方法长这样：

A(x)=∑i=0nai∗xiA(x)=\sum_{i=0}^n a_i*x^iA(x)=∑i=0n​ai​∗xi

然后，有另一种点值表示法，就是用nnn个点来表示。

对于一个点(x,y)(x,y)(x,y)，可以理解成，将xxx带入多项式中，求得的结果是yyy。

其实这nnn个点不一定是真实存在的，因为在FFT中我们用的是复数……

那么，我们可以通过这nnn个点的坐标，然后推出原来的式子。

证明？我觉得这个感性理解一下就好了。

可以看作用nnn个点，定一个nnn次函数。

然后，对于两个多项式相乘，假设两个点为(x,y1)(x,y_1)(x,y1​)和(x,y2)(x,y_2)(x,y2​)

那么它们相乘的结果就是(x,y1∗y2)(x,y_1*y_2)(x,y1​∗y2​)

这个其实也挺好理解，因为这些多项式可以看成函数。

---

算法的大概流程

一、点值运算

就是将多项式的形式转化成点值表示法。

二、逐项相乘

三、插值运算

将多项式由点值表示法转化回去。

---

nnn次单位根

定义

有一个方程：

xn=1x^n=1xn=1

这个方程，人们看到了，肯定会毫不犹豫地想到x=1x=1x=1。如果nnn是偶数，还可以是−1-1−1。

但是，如果我们把范围延伸到复数，那么，就有nnn个根。

我们可以画一个图看一下。



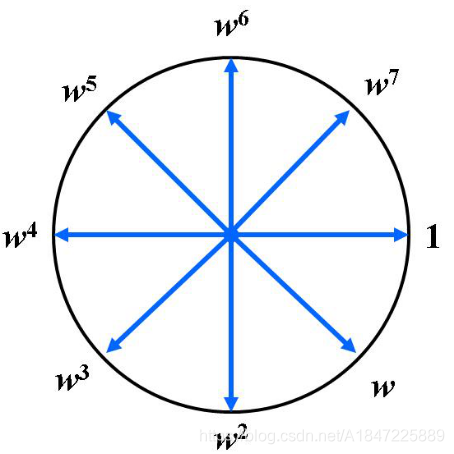
（图片摘自YL的PPT。吐槽一下，为什么和我认识的顺序相反？不过……也没有多大关系，本质上是一样的。）

我们可以发现，这些根围成了一个圆。

这个圆被划分成了nnn等分。

那么它们究竟是多少呢？

首先，

我说一说复数的乘法：

对于一个复数a+bia+bia+bi，其实有另一种写法：l(cos⁡θ+isin⁡θ)l(\cos \theta +i\sin \theta)l(cosθ+isinθ)

这种写法被称为三角表示法，可以用图形理解一下，

lll叫模长，表示这个点到原点的距离。

θ\thetaθ是原点发出经过它的射线和xxx洲的正半轴的夹角（逆时针）。

然后，对于两个复数相乘，就相当于是模长相乘，夹角相加。

证明？我不会证。

当初，在某一位大佬讲FFT时，我问怎么证，他简单地化了一下式子，我问最后一步是为什么，怎么证。他说，很简单，用泰勒级数展开就行了。

我：……

总之就这么用就好了。

那么我们可以发现，如果模长都为111，乘起来是不会变的，只是夹角相加。所以有的时候，它会在转若干次的时候转到(1,0)(1,0)(1,0)。

所以说，我们可以发现上面的这些点统统可以用ωk\omega^kωk来表示。

因为它们围成了一个圆，上一个绕着原点转到某一个固定的角度，就得到下一个。从(1,0)(1,0)(1,0)开始，转nnn次，就会回来。

我们记ωn=ωn1\omega_n=\omega_n^1ωn​=ωn1​，为主nnn次单位根。

性质

1.群的性质ωnjωnk=ωn(j+k)mod  n\omega_n^j\omega_n^k=\omega_n^{(j+k)\mod n}ωnj​ωnk​=ωn(j+k)modn​

这条性质比较显然。因为ωn0=ωnn\omega_n^0=\omega_n^nωn0​=ωnn​。

也可以通过图来理解一下。

2.消去引理ωdndk=ωnk\omega_{dn}^{dk}=\omega_{n}^{k}ωdndk​=ωnk​

这个东西也可以通过图来理解一下。

3.折半引理ωnk+n2=−ωnk\omega_n^{k+\frac{n}{2}}=-\omega_n^kωnk+2n​​=−ωnk​

这个东西还是可以画图理解一下，当然其实也很好证明。

只需要将等式的两边分别平方一下，易得它们的平方相等。

又显然它们不相等（嗯，的确显然）

所以它们一定互为相反数。

好草率的证明啊……

4.求和引理：n∤kn\nmid kn∤k时∑j=0n−1(ωnk)j=0\sum_{j=0}^{n-1}{\left(\omega_n^k\right)}^j=0∑j=0n−1​(ωnk​)j=0，否则∑j=0n−1(ωnk)j=n\sum_{j=0}^{n-1}{\left(\omega_n^k\right)}^j=n∑j=0n−1​(ωnk​)j=n

这个有点复杂，当然，也仅仅是有点复杂……

等比数列求和在复数显然也适用，所以我们直接简单粗暴地强行搬过来：

∑j=0n−1(ωnk)j=(ωnk)n−1ωnk−1=(ωnn)k−1ωnk−1=0\sum_{j=0}^{n-1}{\left(\omega_n^k\right)}^j \\
=\frac{{\left(\omega_n^k\right)}^n-1}{\omega_n^k-1} \\
=\frac{{\left(\omega_n^n\right)}^k-1}{\omega_n^k-1} \\
=0j=0∑n−1​(ωnk​)j=ωnk​−1(ωnk​)n−1​=ωnk​−1(ωnn​)k−1​=0

用处

用处？

多亏了它奇怪的性质，所以才可以用来玩FFT。

这个性质有什么用，看看后面就知道了。

据说，NTT似乎和FFT的原理差不多，只不过用的是某些模数的特殊性质。所以常数很小。

---

DFT

先不要说FFT，从简单的入手。

之前说过这个东西是用来将普通的性质转换成点值表示法。

我们可以将(ωn0,ωn1,......,ωnn−1)(\omega_n^0,\omega_n^1,......,\omega_n^{n-1})(ωn0​,ωn1​,......,ωnn−1​)带入A(x)=∑i=0n−1aixiA(x)=\sum_{i=0}^{n-1}a_i x^iA(x)=∑i=0n−1​ai​xi，

得到(y0,y1,......,yn−1)(y_0,y_1,......,y_{n-1})(y0​,y1​,......,yn−1​)。

显然，yk=∑i=0n−1aiωkiy_k=\sum_{i=0}^{n-1}a_i\omega^{ki}yk​=∑i=0n−1​ai​ωki

IDFT

再讲IDFTIDFTIDFT

我们现在已经知道了A(x)=∑i=0n−1aixiA(x)=\sum_{i=0}^{n-1}a_i x^iA(x)=∑i=0n−1​ai​xi的DFT为(y0,y1,......,yn−1)(y_0,y_1,......,y_{n-1})(y0​,y1​,......,yn−1​)

我们再设B(x)=∑i=0n−1yi∗xiB(x)=\sum_{i=0}^{n-1}y_i*x^iB(x)=∑i=0n−1​yi​∗xi。

我们将(ωn0,ωn−1,.....,ωn−(n−1))({\omega_n^0,\omega_{n}^{-1},.....,\omega_{n}^{-(n-1)}})(ωn0​,ωn−1​,.....,ωn−(n−1)​)带入B(x)B(x)B(x)，又得到一个DFT：(z0,z1,......,zn−1)(z_0,z_1,......,z_{n-1})(z0​,z1​,......,zn−1​)

然后推一波式子：

zk=∑i=0n−1yi(ωn−k)i=∑i=0n−1(∑j=0n−1aj(ωni)j)(ωn−k)i=∑j=0n−1aj(∑i=0n−1(ωnj−k)i)=nakz_k=\sum_{i=0}^{n-1}y_i \left(\omega_n^{-k}\right)^i \\
=\sum_{i=0}^{n-1}\left(\sum_{j=0}^{n-1}a_j \left(\omega_n^i\right)^j\right) \left(\omega_n^{-k}\right)^i\\
=\sum_{j=0}^{n-1} a_j \left(\sum_{i=0}^{n-1}\left(\omega_n^{j-k}\right)^i\right) \\
=n a_kzk​=i=0∑n−1​yi​(ωn−k​)i=i=0∑n−1​(j=0∑n−1​aj​(ωni​)j)(ωn−k​)i=j=0∑n−1​aj​(i=0∑n−1​(ωnj−k​)i)=nak​

其中最后一步用了前面所说的求和引理。

所以ak=zkna_k=\frac{z_k}{n}ak​=nzk​​

你们现在说，为什么要用这些奇奇怪怪的nnn次单位根？如果没有这些奇妙的性质，那么在这时候转换就很不方便了。

我们发现，DFT和IDFT的求法实际上是差不多的（可以套用同一个板子），只是要带进去的东西不同。

FFT

其实FFT是DFT的优化。

DFT的时间复杂度是O(n2)O(n^2)O(n2)的，很慢（人家傅里叶才懒得帮你算时间复杂度呢！）。

所以我们可以用分治的方法来将其优化到O(nlg⁡n)O(n\lg n)O(nlgn)

对于一个多项式A(x)=∑i=0n−1aixiA(x)=\sum_{i=0}^{n-1}a_i x^iA(x)=∑i=0n−1​ai​xi，我们考虑用分治的方式来计算它的DFT。

设A0(x)=a0+a2∗x+......+an−2∗xn2−1,A1(x)=a1+a3∗x+......+an−1∗xn2−1A_0(x)=a_0+a_2*x+......+a_{n-2}*x^{\frac{n}{2}-1},A_1(x)=a_1+a_3*x+......+a_{n-1}*x^{\frac{n}{2}-1}A0​(x)=a0​+a2​∗x+......+an−2​∗x2n​−1,A1​(x)=a1​+a3​∗x+......+an−1​∗x2n​−1

那么我们可以得到A(x)=A0(x2)+xA1(x2)A(x)=A_0(x^2)+xA_1(x^2)A(x)=A0​(x2)+xA1​(x2)

设k&lt;n2k&lt;\frac{n}{2}k<2n​，则

A(ωnk)=A0(ωn2k)+ωnkA1(ωn2k)=A0(ωn2k)+ωnkA1(ωn2k)A(ωnk+n2)=A0(ωn2k+n)+ωnk+n2A1(ωn2k+n)=A0(ωn2k)+ωnk+n2A1(ωn2k)=A0(ωn2k)−ωnkA1(ωn2k)A(\omega_n^k)=A_0(\omega_n^{2k})+\omega_n^k A_1(\omega_n^{2k}) \\
=A_0(\omega_\frac{n}{2}^k)+\omega_n^k A_1(\omega_{\frac{n}{2}}^k) \\
A(\omega_n^{k+\frac{n}{2}})=A_0(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}A_1(\omega_n^{2k+n}) \\
=A_0(\omega_n^{2k})+\omega_n^{k+\frac{n}{2}}A_1(\omega_n^{2k})\\
=A_0(\omega_{\frac{n}{2}}^k)-\omega_n^kA_1(\omega_{\frac{n}{2}}^k)A(ωnk​)=A0​(ωn2k​)+ωnk​A1​(ωn2k​)=A0​(ω2n​k​)+ωnk​A1​(ω2n​k​)A(ωnk+2n​​)=A0​(ωn2k+n​)+ωnk+2n​​A1​(ωn2k+n​)=A0​(ωn2k​)+ωnk+2n​​A1​(ωn2k​)=A0​(ω2n​k​)−ωnk​A1​(ω2n​k​)

我们可以递归地求下去，每次将其分成两半。那么这样子显然是O(nlg⁡n)O(n \lg n)O(nlgn)的。

（当然，在一开始就要将nnn补成2次幂的形式，不然会出现不能分成两个相等的部分的尴尬情况。）

FFT的常数优化

如果真的像上面一样递归处理，那就T飞了。

常数太大了啊！

所以说，我们要对它进行优化。

FFT中位置的变换

设一开始的编号为0,1,2,3,4,5,6,7，变换后的编号为0,4,2,6,1,5,3,7

可以将所有的东西用二进制来搞一搞，然后你就会发现：

对应的位置的二进制形式居然是相反的！

是不是很神奇？

接下来我来简略的证明一下（当然还是感性理解）：

每一次将一大块的东西分成两个小块分别处理。

这时候相当于将编号的第000位为000的放左边，为111的放右边。

可以思考一下，如果将这个新的顺序重新编号，那么，左边的最高位都是000，右边的最高位都是111。

所以相当于是最低位和最高位换了一下。

然后再递归向下处理，后面的东西也是一样的。

其实还挺理性的，不是吗？

那么我们可以通过这个结论，来搞一个自底向上的算法，然后就不需要递归，多么舒服！

蝴蝶变换

好高大上的一个名字，是不是？

但实际上，它就是我们再前面讲过的东西：

A(ωnk)=A0(ωn2k)+ωnkA1(ωn2k)A(ωnk+n2)=A0(ωn2k)−ωnkA1(ωn2k)A(\omega_n^k)
=A_0(\omega_\frac{n}{2}^k)+\omega_n^k A_1(\omega_{\frac{n}{2}}^k) \\
A(\omega_n^{k+\frac{n}{2}})
=A_0(\omega_{\frac{n}{2}}^k)-\omega_n^kA_1(\omega_{\frac{n}{2}}^k)A(ωnk​)=A0​(ω2n​k​)+ωnk​A1​(ω2n​k​)A(ωnk+2n​​)=A0​(ω2n​k​)−ωnk​A1​(ω2n​k​)

可以发现，对于左边的两个东西，转移到它们的两个量是可以一起用的。

如果你画一张图来理解一下，那么你就会发现，这个东西真的很像蝴蝶。

真的好像哟……

这个东西在程序实现的时候直接用上就好了。

在我的印象中，蝴蝶变换本来就是FFT的转移，所以告诉我，为什么还有不用蝴蝶变换的非递归FFT程序？可能是我智商太低，理解不了更差的解法（手动滑稽）。

---

补充

二进制形式相反的怎么弄？

不要想得太多，直接预处理，暴力不会爆炸。

时间复杂度还是一样的……

主nnn次单位根怎么算？

数形结合……

因为这个半径为111的圆被划成了nnn等分。

所以每个角就是2πn\frac{2\pi}{n}n2π​。

那么ωn=cos⁡2πn+itan⁡2πn\omega_n=\cos\frac{2\pi}{n}+i\tan\frac{2\pi}{n}ωn​=cosn2π​+itann2π​。

这是一种比较好理解的方法。

但是还有一种很变态，很奇怪，很强大的方法：

ωn=e2πin\omega_n=e^{\frac{2\pi i}{n}}ωn​=en2πi​

这是什么鬼？？？

据说脑洞数学家欧拉，他研究出来这么一个玩意：exi=cos⁡x+itan⁡xe^{x i}=\cos x+i\tan xexi=cosx+itanx

所以说e2πin=cos⁡2πn+itan⁡2πne^{\frac{2\pi i}{n}}=\cos \frac{2\pi}{n}+i\tan \frac{2\pi}{n}en2πi​=cosn2π​+itann2π​对吧……

可是原理是什么……还有，如果直接打上这种东西，那么你要用C++自带的<complex>啊！

复数的实现

刚刚还提起过，C++自带了一个叫<complex>的库。

其实自己重载运算符打得更加舒服……吧！

至少我相信手打绝对比自带的快！

注意精度问题

这个不用说了吧……

---

代码实现（易懂&常数大版）

using namespace std;
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define N 1000000
#define PI 3.14159265358979
struct com{
	double a,b;
	com(double _a=0,double _b=0){a=_a,b=_b;}
};
inline com operator+(const com &x,const com &y){return com(x.a+y.a,x.b+y.b);}
inline com operator-(const com &x,const com &y){return com(x.a-y.a,x.b-y.b);}
inline com operator*(const com &x,const com &y){return com(x.a*y.a-x.b*y.b,x.a*y.b+x.b*y.a);}
inline com operator/(const com &x,const double y){return com(x.a/y,x.b/y);}
int n,m,an,bn;
com a[1<<21],b[1<<21],c[1<<21];
int re[1<<21];
inline void init();
inline void fft(com*,int);
int main(){
	scanf("%d%d",&an,&bn);
	for (int i=0;i<=an;++i){
		int tmp;
		scanf("%d",&tmp);
		a[i]=com(tmp,0);
	}
	for (int i=0;i<=bn;++i){
		int tmp;
		scanf("%d",&tmp);
		b[i]=com(tmp,0);
	}
	for (n=1,m=0;n<=an+bn;n<<=1,m++);//开够足够的n
	init();
	fft(a,1);
	fft(b,1);
	for (int i=0;i<n;++i)
		c[i]=a[i]*b[i];
	fft(c,-1);
	for (int i=0;i<=an+bn;++i)
		printf("%d ",int(c[i].a+0.5));//精度问题……你会发现有一种很尴尬的情况中，输出实数会出现-0
	return 0;
}
inline void init(){//计算每个编号用二进制翻转过来是是什么（想不到什么直接用位运算的巧妙方法）
	for (int i=0;i<n;++i){
		int tmp=0;
		for (int j=0,k=i;j<m;++j,k>>=1)
			tmp=(tmp<<1)+(k&1);
		re[i]=tmp;
	}
}
inline void fft(com* a,int flag){
	for (int i=0;i<n;++i)
		if (i<re[i])
			swap(a[i],a[re[i]]);
	for (int i=1;i<n;i<<=1){//i表示从长度为i的区间转移到长度为i*2的区间
		com wn(cos(flag*PI/i),sin(flag*PI/i));//求主i*2次单位根（注意是i*2次！）
		for (int j=0;j<n;j+=i<<1){//分段来枚举
			com wnk(1,0);
			for (int k=j;k<j+i;++k,wnk=wnk*wn){
				//以下为蝴蝶变换
				com x=a[k],y=wnk*a[k+i];
				a[k]=x+y;
				a[k+i]=x-y;
			}
		}
	}
	if (flag==-1)
		for (int i=0;i<n;++i)
			a[i]=a[i]/n;
}

至于常数小的代码，我真的不会码……

我的这个代码在洛谷的模板题上跑2000+ms，而题目说最好在1000ms以内通过。

审视了半天，没有发现什么优化了之后有特别大的作用的修改方法。

然后，我试着用YL标程里的方法打一遍。YL的标程中FFT的枚举方式和我的不太一样。

我也是着这样打一遍，然后我就发现更慢了……可能是因为他在枚举的过程中没有一个紧接着一个枚举（因为有高速缓存，所以顺序访问数组自然会比跳着访问数组要快）

自己打的程序常数终究是比人家的大啊……

---

参考资料

FFT详解 - 总理同学的编程尝试 - CSDN博客

小学生都能看懂的FFT!!! - 胡小兔 - 博客园