codeforces 922 B. Magic Forest（枚举、位运算（异或））

题目链接：点击打开链接

Imp is in a magic forest, where xorangles grow (wut?)

A xorangle of order n is such a non-degenerate triangle, that lengths of its sides are integers not exceeding n, and the xor-sum of the lengths is equal to zero. Imp has to count the number of distinct xorangles of order n to get out of the forest.

Formally, for a given integer n you have to find the number of such triples (a, b, c), that:

• 1 ≤ a ≤ b ≤ c ≤ n;
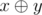• , where  denotes the bitwise xor of integers x and y.
• (a, b, c) form a non-degenerate (with strictly positive area) triangle.

Input

The only line contains a single integer n (1 ≤ n ≤ 2500).

Output

Print the number of xorangles of order n.

Examples

input

Copy

6

output

1

input

Copy

10

output

2

Note

The only xorangle in the first sample is (3, 5, 6).

题意：没错这就是一个枚举三角形三条边的题目，不过由于要求a ^ b ^ c = 0，所以这一题只需要o(n²)就能枚举完

下面来看这条件啥意思：我们先看两个值异或啥意思，a^ b = 0 ：异或异或，a和b的二进制每一位异的话就是1，不异的话就是0，a^b也就是说a和b的每一位都相同，也就是a == b！

那么a^b^c=0啥意思？将a^b看成一个整体呗，也就是三角形的第三条边的值为a^b，只要保证a^b满足第三条边就阔以了。

其他还有啥坑点？我们来学下英语。。

xor 异或

non-degenerate triangle 非退化三角形， 也就是正常的三角形，没有180度甚至以上的角的三角形。

⊕ 这符号也是异或。。

我们顺便来看下异或的其他性质吧

1. a ⊕ a = 0

2. a ⊕ b = b ⊕ a

3. a ⊕b ⊕ c = a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c;

4. d = a ⊕ b ⊕ c 可以推出 a = d ⊕ b ⊕ c.

5. a ⊕ b ⊕ a = b.

其实现场想一下推到还是能推出来的  

这题就不贴代码了。。