[BZOJ2876]骑行川藏
以前并没有发现微积分教材上有这种东西...我还是太菜了...
其实就是要在满足$\sum\limits_{i=1}^nk_is_i(v_i-v_i')^2\leq E$的同时求$\sum\limits_{i=1}^n\dfrac{s_i}{v_i}$的最小值
首先我们要跑得尽可能快,所以$v_i\geq v_i'$,而且在最优解体能是一定会被用完的,那么限制就变成等式了
拉格朗日乘数法可用于求多元函数的带限制极值:$g(x_1,\cdots,x_n)=0$,求$f(x_1,\cdots,x_n)$的极值
我看的书上有一个挺好的几何解释:把$f$的图像画出来,再在上面画一些“等高线”,同时把$g(x_1,\cdots,x_n)=0$和$f(x_1,\cdots,x_n)$的“交线”画出来,那么取到极值的地方就是等高线与交线相切的地方
比如说求$f(x,y)=x^2+y^2+2$在限制$g(x,y)=x^2+\dfrac14y^2-1=0$下的极值,三张图一目了然
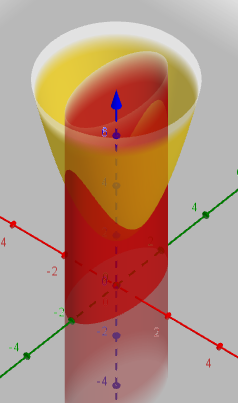 黄色:$z=f(x,y)$,红色:$g(x,y)=0$
黄色:$z=f(x,y)$,红色:$g(x,y)=0$
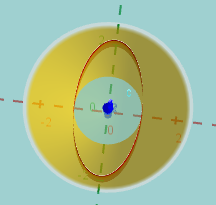 $z=2$
$z=2$
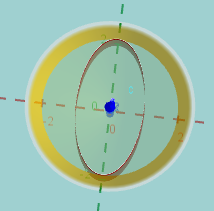 $z=6$
$z=6$
相切意味着梯度线性相关,即是说如果在$x_i=t_i$处$f$取得极值,那么$\nabla f(t_1,\cdots,t_n)=\lambda\nabla g(t_1,\cdots,t_n)$,我们把它拆分成关于每个变量的偏导,即对于$\forall1\leq i\leq n$有$\left.\dfrac{\partial f}{\partial x_i}\right|_{x_i=t_i}=\lambda\left.\dfrac{\partial g}{\partial x_i}\right|_{x_i=t_i}$
再加上$g(t_1,\cdots,t_n)=0$,总共$n+1$个变量和$n+1$条方程,可以解出来
再看这道题,限制条件是$\sum\limits_{i=1}^nk_is_i(v_i-v_i')^2-E=0$,我们要求$\sum\limits_{i=1}^n\dfrac{s_i}{v_i}$的极值,所以有方程$-\dfrac1{v_i^2}=2\lambda k_i(v_i-v_i')$,首先这说明$\lambda\lt0$,方程左边是经过三四象限的类双曲线,右边是斜率为负的经过第一象限的直线,所以当$\lambda$确定后有且只有一个$v_i$满足方程,并且因为$\lambda$越大,$v_i$也越大,这直接导致了$\sum\limits_{i=1}^nk_is_i(v_i-v_i')^2$变大,所以我们可以二分出满足关于$E$的限制的$\lambda$,在这个过程中求$v_i$也是可以二分的,于是我们就愉悦地做完了这题
注意精度...
#include<stdio.h>
typedef double du;
const du eps=1e-14,inf=1e9;
du s[10010],k[10010],v[10010];
int n;
du sqr(du x){return x*x;}
du calc(int i,du lm){
du l,r,mid;
l=eps;
r=inf;
while(r-l>eps){
mid=(l+r)*.5;
if(-1<2*lm*k[i]*(mid-v[i])*sqr(mid))
l=mid;
else
r=mid;
}
return mid;
}
du check(du lm){
int i;
du r=0;
for(i=1;i<=n;i++)r+=k[i]*s[i]*sqr(calc(i,lm)-v[i]);
return r;
}
int main(){
int i;
du E,l,r,mid,ans;
scanf("%d%lf",&n,&E);
for(i=1;i<=n;i++)scanf("%lf%lf%lf",s+i,k+i,v+i);
l=-inf;
r=-eps;
while(r-l>eps){
mid=(l+r)*.5;
if(check(mid)<E)
l=mid;
else
r=mid;
}
ans=0;
for(i=1;i<=n;i++)ans+=s[i]/calc(i,mid);
printf("%.10lf",ans);
}
[BZOJ2876]骑行川藏的更多相关文章
- 【BZOJ2876】【NOI2012】骑行川藏(数学,二分答案)
[BZOJ2876][NOI2012]骑行川藏(数学,二分答案) 题面 BZOJ 题解 我们有一个很有趣的思路. 首先我们给每条边随意的赋一个初值. 当然了,这个初值不会比这条边的风速小. 那么,我们 ...
- bzoj 2876: [Noi2012]骑行川藏 拉格朗日数乘
2876: [Noi2012]骑行川藏 Time Limit: 20 Sec Memory Limit: 128 MBSec Special JudgeSubmit: 1033 Solved: ...
- 高等数学(拉格朗日乘子法):NOI 2012 骑行川藏
[NOI2012] 骑行川藏 输入文件:bicycling.in 输出文件:bicycling.out 评测插件 时间限制:1 s 内存限制:128 MB NOI2012 Day1 Des ...
- BZOJ 2876 【NOI2012】 骑行川藏
题目链接:骑行川藏 听说这道题需要一些高数知识 于是膜了一发dalao的题解……然后就没了…… 不要吐槽我的精度TAT……eps设太小了就TLE,大了就Wa……我二分的边界是对着数据卡的…… 下面贴代 ...
- 「NOI2012」骑行川藏
「NOI2012」骑行川藏 题目描述 蛋蛋非常热衷于挑战自我,今年暑假他准备沿川藏线骑着自行车从成都前往拉萨. 川藏线的沿途有着非常美丽的风景,但在这一路上也有着很多的艰难险阻,路况变化多端,而蛋蛋的 ...
- bzoj2876 [Noi2012]骑行川藏
Description 蛋蛋非常热衷于挑战自我,今年暑假他准备沿川藏线骑着自行车从成都前往拉萨.川藏线的沿途有着非常美丽的风景,但在这一路上也有着很多的艰难险阻,路况变化多端,而蛋蛋的体力十分有限,因 ...
- bzoj2876 [NOI2012]骑行川藏(拉格朗日乘数法)
题目描述 蛋蛋非常热衷于挑战自我,今年暑假他准备沿川藏线骑着自行车从成都前往拉萨.川藏线的沿途有着非常美丽的风景,但在这一路上也有着很多的艰难险阻,路况变化多端,而蛋蛋的体力十分有限,因此在每天的骑行 ...
- 2876: [Noi2012]骑行川藏 - BZOJ
Description 蛋蛋非常热衷于挑战自我,今年暑假他准备沿川藏线骑着自行车从成都前往拉萨.川藏线的沿途有着非常美丽的风景,但在这一路上也有着很多的艰难险阻,路况变化多端,而蛋蛋的体力十分有限,因 ...
- 【NOI2012】骑行川藏
获得成就:第一次在信竞做神仙数学题 先放个前言,$OI$ 出大型数学题还是比较麻烦的,因为主要是考你数学推导 / 手算式子,你算出来之后把公式套个板子,就得到结论——$OI$ 的大型数学题的代码都是板 ...
随机推荐
- [fzu 2273]判断两个三角形的位置关系
首先判断是否相交,就是枚举3*3对边的相交关系. 如果不相交,判断包含还是相离,就是判断点在三角形内还是三角形外.两边各判断一次. //http://acm.fzu.edu.cn/problem.ph ...
- hbase集群写不进去数据的问题追踪过程
hbase从集群中有8台regionserver服务器,已稳定运行了5个多月,8月15号,发现集群中4个datanode进程死了,经查原因是内存 outofMemory了(因为这几台机器上部署了spa ...
- ansible 部署jdk
playbook 剧本如下 [root@sz_fy_virt_encrypt_33_239 x]# cat jdk.yml - hosts: web remote_user: opsadmin bec ...
- ubuntu安装GraphicsMagick
一. sudo apt-get install graphicsmagick 二. http://www.cnblogs.com/cocowool/archive/2010/08/16/1800954 ...
- a 标签中 title 属性样式修改
无文字描述,直接上测试页,看效果. <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" " ...
- [洛谷P1541] 乌龟棋
洛谷题目链接:乌龟棋 题目背景 小明过生日的时候,爸爸送给他一副乌龟棋当作礼物. 题目描述 乌龟棋的棋盘是一行N个格子,每个格子上一个分数(非负整数).棋盘第1格是唯一的起点,第N格是终点,游戏要求玩 ...
- 【Foreign】哈密顿回路 [MIM]
哈密顿回路 Time Limit: 15 Sec Memory Limit: 256 MB Description Input Output Sample Input 4 10 0 3 2 1 3 ...
- codeforces613B - Skills &&金中市队儿童节常数赛
题目传送门 本随笔写的是第二题...... 这道题方法就是搞乱....因为n较mxa小 所以枚举达到最大上限的点 然后就乱搞 代码看看咯 #include<cstdio> #include ...
- windows支持applocker的版本
Operating system requirements The following table show the on which operating systems AppLocker fe ...
- Pycharm2017汉化包下载链接
https://github.com/ewen0930/PyCharm-Chinese/tree/f5a8dc4a8f34398e81a69c69bb046aa4eff27c90 1.首先下载PyCh ...
