Deep Learning 学习笔记（4）：Logistic Regression 逻辑回归

逻辑回归主要用于解决分类问题，在现实中有更多的运用，

正常邮件or垃圾邮件

车or行人

涨价or不涨价

用我们EE的例子就是：

高电平or低电平

同时逻辑回归也是后面神经网络到深度学习的基础。

（原来编辑器就有分割线的功能啊……）

---

一、Logistic Function（逻辑方程）

同线性回归，我们会有一个Hypothesis Function对输入数据进行计算已得到一个输出值。

考虑到分类问题的特点，常用的函数有sigmoid方程（又叫logistic方程）

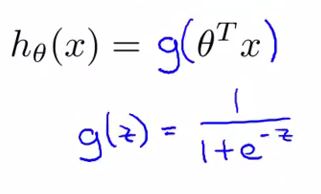
其函数图像如下

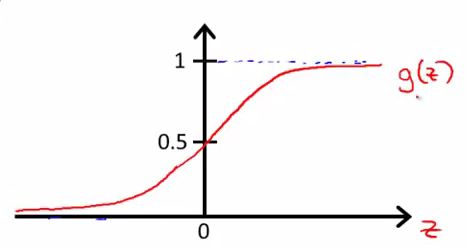
可见：

1、输出区间为（0，1）；

2、对于所有输入 z<0, g(z) < 0.5 ; 对所有输入 z>0, g(z) > 0.5。

因此我们可以把输出 g(z) 看作是一种概率，

当输入 z > 0 ，概率 g(z)>50% 时， 假设成立。

（ 另有tanh函数，输出区间是(-1,1) ）

---

二、Cost Function代价方程

problem：

在逻辑回归中，由于输入和输出不再是线性关系，

如果我们再使用预测值与实际值的欧式距离的均值作为代价方程，

代价方程将会出现多个局部最优点，

这对梯度下降算法来说真是毁灭性的打击。

如图，左边是不理想的cost function ，右边是理想的cost function

（看到右下角的署名没有？ 那才是这些图的真正作者啊，膜拜ing~~）

　　解决方法：

为了解决这个问题，在逻辑回归中，我们使用以下方程作为梯度下降的cost function：（*注释1）

当然这么写还真是不美观，码代码的时候还要加一个逻辑判定语句。

这么些就好多了：

这个函数的叫做 softmax(索夫曼)函数 ，所以在有时候我们又可以把用到这种cost function的回归成为softmax回归。

对应的偏导计算方法如下：

考虑到视频上面没有加上推导过程，但是貌似有公司面试会面这个的推导，我这里放上我无限难看的手写版：

知道了cost function，知道了偏导之后，让我们一起gradient descent吧！

---

附： Decision Boundary

在坐标系中把数据标出，并作出Htheta(x)=0.5的函数曲线

曲线将大致将数据按照标签分为两部分，这就是数据的decision boundary。

---

注释1：在NG的视频中并没有太多讨论为什么使用对数函数。在李航老师的《统计学习》的逻辑回归一章中，我们可以知道在逻辑回归模型中事件几率Y=1（发生概率/不发生概率）是输入x的线性函数（W*x）。即对数方程使逻辑回归模型线性可分。但是后面讲到cost的时候又没讲到两者的的联系，希望网友告知为何。