【sgu390】数位dp

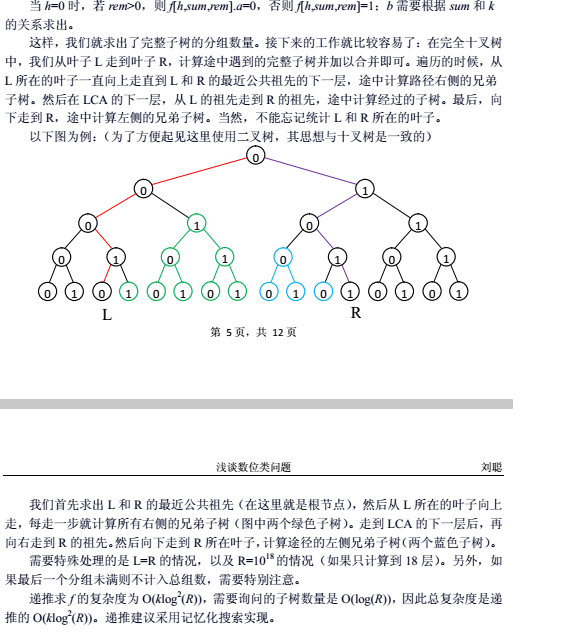
这题其实就是不断地合并子树，跟前面例一的思想是一样的。

这个打法我觉得非常优美啊（学别人的），为什么要搞lim1和lim2呢？

是因为在区间lim1~lim2之外的都是没有用的，但是我们f[h][sum][rem]里存的是一棵完整的h层的树，所以被lim1和lim2限制的就不存进去了。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

typedef long long LL;
const LL N=;
LL l,r,K;
struct node{
    LL a,b;
    bool bk;
    node()
    {
        bk=;a=;b=;
    }
}f[][N][N];
LL dl[],dr[];

void mercy(node &x,node y){x.a+=y.a;x.b=y.b;}

node dp(LL h,LL sum,LL rem,LL lim1,LL lim2)
{
    node ans;
    ans.a=;ans.b=rem;
    if(f[h][sum][rem].bk && !lim1 && !lim2) return f[h][sum][rem];
    if(h==)
    {
        if(sum+rem>=K) ans.a=,ans.b=;
        else ans.a=,ans.b=sum+rem;
    }
    else
    {
        LL x=lim1 ? dl[h] : ;
        LL y=lim2 ? dr[h] : ;
        for(LL i=x;i<=y;i++)
        {
            mercy(ans,dp(h-,sum+i,ans.b,(lim1&(i==x)),(lim2&(i==y))));
        }
    }
    if(!lim1 && !lim2) f[h][sum][rem]=ans,f[h][sum][rem].bk=;
    return ans;
}

int main()
{
    freopen("a.in","r",stdin);
    freopen("me.out","w",stdout);
    scanf("%lld%lld%lld",&l,&r,&K);
    LL x;
    memset(dl,,sizeof(dl));
    memset(dr,,sizeof(dr));
    x=;while(l) {dl[++x]=l%;l/=;}
    x=;while(r) {dr[++x]=r%;r/=;}
    printf("%lld\n",dp(,,,,).a);
    return ;
}