数据结构7——BFS

一、重拾关键

宽度优先搜索，也有称为广度优先搜索，简称BFS。类似于树的按层次遍历的过程。

初始状态：图G所有顶点均未被访问过，任选一点v。

遍历过程：假设从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问，直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。换句话说，广度优先搜索遍历图的过程中以v为起始点，由近至远，依次访问和v有路径相通且路径长度为1,2,…的顶点。

二、算法过程

以如下图的无向图G4为例，进行图的宽度优先搜索：

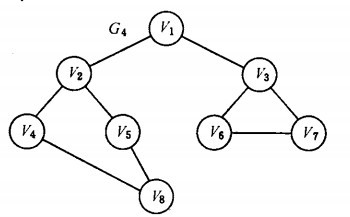
假设从顶点v₁出发进行搜索，首先访问v₁和v₁的邻接点v₂和v₃，然后依次访问v₂的邻接点v₄和v₅及v₃的邻接点v₆和v₇，最后访问v₄的邻接点v₈。由于这些顶点的邻接点均已被访问，并且图中所有顶点都被访问，由些完成了图的遍历。得到的顶点访问序列为：。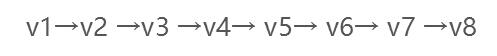

和深度优先搜索类似，在遍历的过程中也需要一个访问标志数组。并且，为了顺次访问路径长度为2、3、…的顶点，需附设队列以存储已被访问的路径长度为1、2、… 的顶点。

三、代码实现

邻接矩阵做存储结构时，广度优先搜索的代码如下。

/*    图的BFS遍历    */
//邻接矩阵形式实现
//顶点从1开始
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int maxn = 105;        //最大顶点数
typedef int VertexType;     //顶点类型
bool vis[maxn];  

struct Graph{               //邻接矩阵表示的图结构
    VertexType vex[maxn];   //存储顶点
    int arc[maxn][maxn];    //邻接矩阵
    int vexnum,arcnum;      //图的当前顶点数和弧数
};

void createGraph(Graph &g)  //构建有向网g
{
    cout<<"请输入顶点数和边数：";
    cin>>g.vexnum>>g.arcnum;

    //构造顶点向量
    cout<<"请依次输入各顶点：\n";
    for(int i=1;i<=g.vexnum;i++){
        scanf("%d",&g.vex[i]);
    }

    //初始化邻接矩阵
    for(int i=1;i<=g.vexnum;i++){
        for(int j=1;j<=g.vexnum;j++){
            g.arc[i][j] = 0;
        }
    }

    //构造邻接矩阵
    VertexType u,v;     //分别是一条弧的弧尾(起点)和弧头(终点)
    printf("每一行输入一条弧依附的顶点（空格分开）：\n");
    for(int i=1;i<=g.arcnum;i++){
        cin>>u>>v;
        g.arc[u][v] = g.arc[v][u] = 1;
    }
}

//邻接矩阵的宽度遍历操作
void BFSTraverse(Graph g)
{
    queue<int> q;                        //声明队列q
    for(int i=1;i<=g.vexnum;i++){
        vis[i] = false;
    }
    for(int i=1;i<=g.vexnum;i++){        //对每个顶点做循环
        if(!vis[i]){
            vis[i] = true;
            printf("%d\t",g.vex[i]);
            q.push(i);                    //将此节点入队列
            while(!q.empty()){
                int m = q.front();
                q.pop();                //出队列，值已赋给m
                for(int j=1;j<=g.vexnum;j++){
                    if(g.arc[m][j]==1 && !vis[j]){        //如果顶点j是顶点i的未访问的邻接点
                        vis[j] = true;
                        printf("%d\t",g.vex[j]);
                        q.push(j);                        //将顶点j入队列
                    }
                }

            }
        }
    }

} 

int main()
{
    Graph g;
    createGraph(g);
    BFSTraverse(g);
    return 0;
}

我的代码2：

 int n, m;
 int graph[][];
 bool vis[];
 queue<int> q;

 void init()
 {
     memset(map,,sizeof(map));
     memset(vis,,sizeof(vis));
     while(!q.empty())   q.pop();
 }

 void BFS(int u)
 {
     vis[u] = ;
     cout<<u<<"\t";
     q.push(u);
     while(!q.empty()){
         int p = q.front();
         q.pop();
         for(int i=;i<=n;i++){
             if(!vis[i] && graph[p][i]==){
                 q.push(i);
                 cout<<i<<"\t";
                 vis[i] = ;
             }
         }
     }
 }

 void read()
 {
     init();
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int u, v;
         cin>>u>>v;
         graph[u][v] = graph[v][u] = ;
     }
     for(int i=;i<=n;i++){
         if(!vis[i])
             BFS(i);
     }
     cout<<endl;
 }

 int main()
 {
     read();
     return ;
 }

对于邻接表的广度优先遍历，代码与邻接矩阵差异不大， 代码如下。

//邻接表的广度遍历算法
void BFSTraverse(GraphList g)
{
    int i;
    EdgeNode *p;
    Queue q;
    for(i = 0; i < g.numVertexes; i++)
    {
        visited[i] = FALSE;
    }
    InitQueue(&q);
    for(i = 0; i < g.numVertexes; i++)
    {
        if(!visited[i])
        {
            visited[i] = TRUE;
            printf("%c ", g.adjList[i].data);   //打印顶点，也可以其他操作
            EnQueue(&q, i);
            while(!QueueEmpty(q))
            {
                int m;
                DeQueue(&q, &m);
                p = g.adjList[m].firstedge;     找到当前顶点边表链表头指针
                while(p)
                {
                    if(!visited[p->adjvex])
                    {
                        visited[p->adjvex] = TRUE;
                        printf("%c ", g.adjList[p->adjvex].data);
                        EnQueue(&q, p->adjvex);
                    }
                    p = p->next;
                }
            }
        }
    }
}

分析上述算法，每个顶点至多进一次队列。遍历图的过程实质是通过边或弧找邻接点的过程，因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同，两者不同之处仅仅在于对顶点访问的顺序不同。

四、沙场练兵

题目一、迷宫问题