SQL夯实基础（五）：索引的数据结构

　　数据量达到十万级别以上的时候，索引的设置就显得异常重要，而如何才能更好的建立索引，需要了解索引的结构等基础知识。本文我们就来讨论索引的结构。

二叉搜索树：binary search tree

1.所有非叶子结点至多拥有两个儿子（Left和Right）；

2.所有结点存储一个关键字；

3.非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；

‍

B树的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字；

如果B树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么B树的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变B树结构（插入与删除结点）不需要移动大段的内存数据，甚至通常是常数开销；

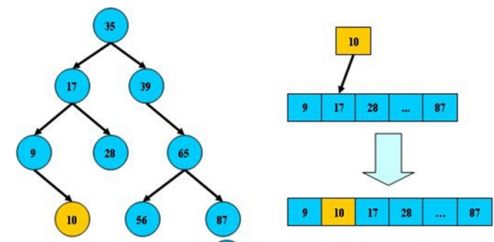
但B树在经过多次插入与删除后，有可能导致不同的结构：

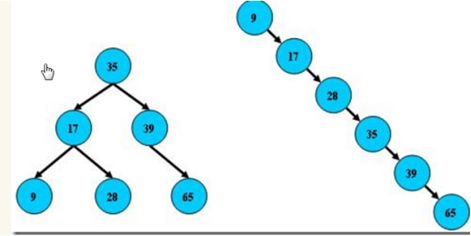
右边也是一个B树，但它的搜索性能已经是线性的了；同样的关键字集合有可能导致不同的树结构索引；所以，使用B树还要考虑尽可能让B树保持左图的结构，和避免右图的结构，也就是所谓的“平衡”问题；

实际使用的B树都是在原B树的基础上加上平衡算法，即“平衡二叉树”；如何保持B树结点分布均匀的平衡算法是平衡二叉树的关键；平衡算法是一种在B树中插入和删除结点的策略；

B-树

B-tree，即B树，而不要读成B减树，它是一种多路搜索树（并不是二叉的）：

1.定义任意非叶子结点最多只有M个儿子；且M>2；

2.根结点的儿子数为[2, M]；

3.除根结点以外的非叶子结点的儿子数为[M/2, M]；

4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

5.非叶子结点的关键字个数=指向儿子的指针个数-1；

6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

8.所有叶子结点位于同一层；

如：（M=3）

‍

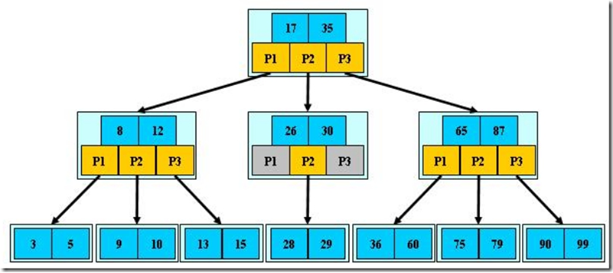
B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点；

B-树的特性：

1.关键字集合分布在整颗树中；

2.任何一个关键字出现且只出现在一个结点中；

3.搜索有可能在非叶子结点结束；

4.其搜索性能等价于在关键字全集内做一次二分查找；

5.自动层次控制；

由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少利用率，其最底搜索性能为：

‍

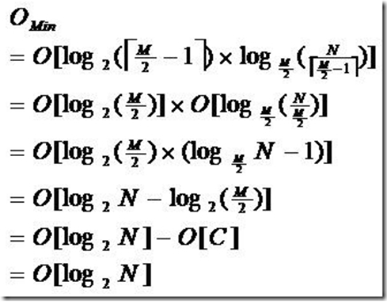
其中，M为设定的非叶子结点最多子树个数，N为关键字总数；

所以B-树的性能总是等价于二分查找（与M值无关），也就没有B树平衡的问题；

由于M/2的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并；

B+树

B+树是B-树的变体，也是一种多路搜索树：

其定义基本与B-树同，

除了：

1.非叶子结点的子树指针与关键字个数相同；

2.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B-树是开区间）；（B+是闭区间，也就是包含区间的两端值）

3.为所有叶子结点增加一个链指针；

4.所有关键字都在叶子结点出现；

如：（M=3）

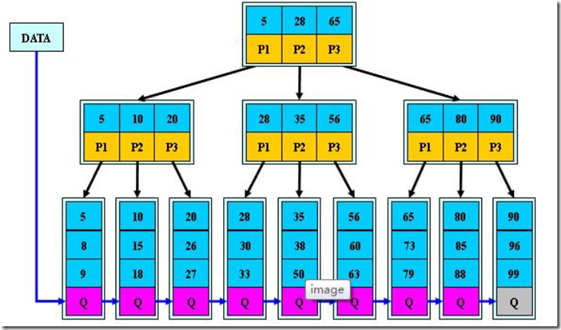
B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

B+的特性：

1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；

2.不可能在非叶子结点命中；

3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；

4.更适合文件索引系统；

原因：相对于B树，（1）B+树空间利用率更高，因为B+树的内部节点只是作为索引使用，而不像B-树那样每个节点都需要存储硬盘指针。

（2）增删文件（节点）时，效率更高，因为B+树的叶子节点包含所有关键字，并以有序的链表结构存储，这样可很好提高增删效率。

聚集索引和非聚集索引

　　聚集索引和非聚集索引都采用了B+树的结构，但非聚集索引的叶子层并不与实际的数据页相重叠，而采用叶子层包含一个指向表中的记录在数据页中的指针的方式。

　　聚集索引和非聚集索引的根本区别是表记录的排列顺序和与索引的排列顺序是否一致，聚集索引表记录的排列顺序与索引的排列顺序一致，优点是查询速度快，因为一旦具有第一个索引值的纪录被找到，具有连续索引值的记录也一定物理的紧跟其后。

　　聚集索引的缺点是对表进行修改速度较慢，这是为了保持表中的记录的物理顺序与索引的顺序一致，而把记录插入到数据页的相应位置，必须在数据页中进行数据重排，降低了执行速度。

　　非聚集索引指定了表中记录的逻辑顺序，但记录的物理顺序和索引的顺序不一致，聚集索引和非聚集索引都采用了B+树的结构，但非聚集索引的叶子层并不与实际的数据页相重叠，而采用叶子层包含一个指向表中的记录在数据页中的指针的方式。非聚集索引比聚集索引层次多，添加记录不会引起数据顺序的重组。

简单的理解：聚集索引..就像我们新华字典中的按拼音排序..即你查.."爱"字..可以在前面看到"癌"字，而非聚集索引就是新华字典中的按部首笔划排序。

　　聚集索引确定表中数据的物理顺序。聚集索引类似于电话簿，后者按姓氏排列数据。由于聚集索引规定数据在表中的物理存储顺序，因此一个表只能包含一个聚集索引。但该索引可以包含多个列（组合索引），就像电话簿按姓氏和名字进行组织一样。

非聚集索引与课本中的索引类似。数据存储在一个地方，索引存储在另一个地方，索引带有指针指向数据的存储位置。索引中的项目按索引键值的顺序存储，而表中的信息按另一种顺序存储（这可以由聚集索引规定）。

索引的建立原则

避免添加不必要的列。

每页上能容纳更多的行。

维护索引

　　由于索引是采用 B 树结构存储的，所以对应的索引项并不会被删除，经过一段时间的增删改操作后，数据库中就会出现大量的存储碎片，这和磁盘碎片、内存碎片产生原理是类似的，这些存储碎片不仅占用了存储空间，而且降低了数据库运行的速度。如果发现索引中存在过多的存储碎片的话就要进行“碎片整理”了，最方便的“碎片整理” 手段就是重建索引， 重建索引会将先前创建的索引删除然后重新创建索引，主流数据库管理系统都提供了重建索引的功能，比如 REINDEX、REBUILD 等，如果使用的数据库管理系统没有提供重建索引的功能，可以首先用DROP INDEX语句删除索引，然后用ALTER TABLE 语句重新创建索引。