T406696 『STA - R4』冰红茶 题解

题目链接：冰红茶

比较有意思的套路题(前提是接触过)

首先，一个最基本的线段树包含两种操作的板子要会，分别为区间赋值与区间加，同时维护区间最值。这个挺简单的，区间赋值优先级高于区间加，可以将区间加覆盖为 \(0\) 以后再进行加就行了。其实就是这个题：P1253 扶苏的问题。

看到操作 \(2\) 的删除很多人不知道怎么解决，其实这是一类经典的问题可以看：

P4145 上帝造题的七分钟 2 / 花神游历各国 题解 或者 P9989 [Ynoi Easy Round 2023] TEST_69 题解。

操作一

分块和线段树都可以，这里用线段树，讲讲这题怎么做。我们注意操作一其实掺杂着两种操作：显而易见的是，我们可以维护两种和的区间最大值，分别表示两种冰红茶的和的区间最大值。我们来观察每次操作一有什么影响？很显然的是，操作一如果对某种区间和下手，会使得另一种被清空。也就是说，每次操作一其实有两个效果，一个是某种区间和增加，另一种是被覆盖为 \(0\)。那其实操作一我们只需要维护两个操作：区间加和区间赋值。比较简单的是，区间赋值是只会赋值为 \(0\)，所以我们用布尔标记即可。

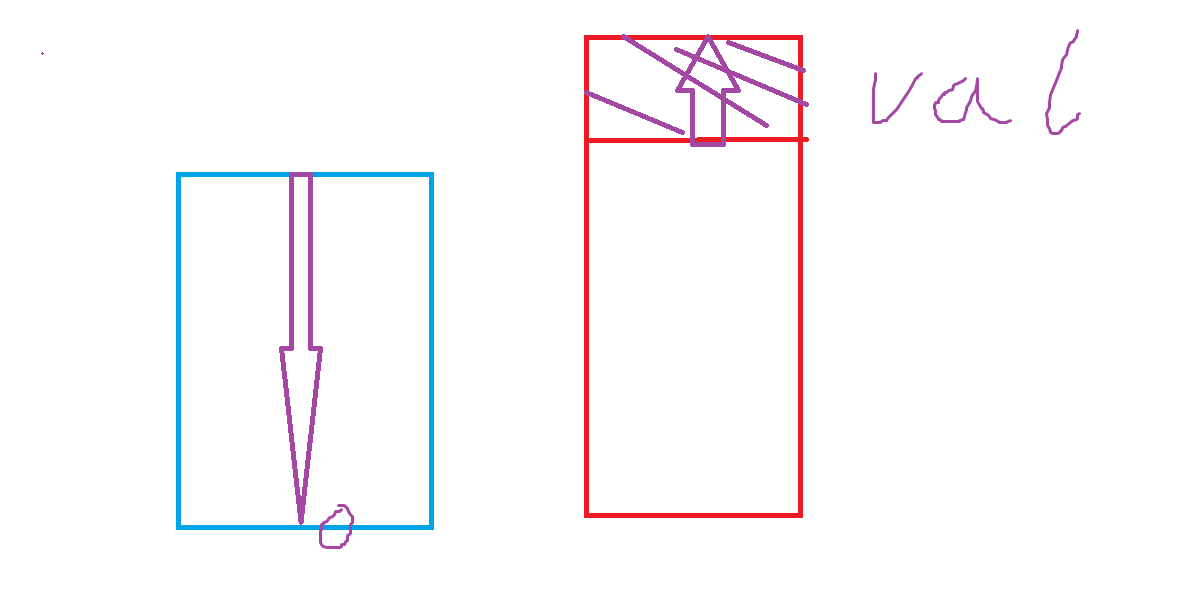
如图所示，每个线段树节点维护两种冰红茶的区间最大值，当加入一个 \(val\) 比如红色冰红茶时，另一种需要区间被覆盖为 \(0\)，红色则增加 \(val\)。我们为两种冰红茶维护三种信息：

1. 区间最值。表示这种冰红茶的区间最值。

2. 区间加标记。表示这种冰红茶的加懒标记。

3. 区间覆盖标记。表示这种冰红茶需要覆盖为 \(0\) 的覆盖懒标记。

操作二

如果做过我发的那两个题，操作二就比较简单了。考虑到每个点至多删除一次，我们可以考虑维护一些信息来快速判断一个区间内是否有需要删除的点。考虑到查询操作要查询未被删除的点的总数量，我们可以将每个点初始赋值为 \(1\)，同时维护区间最值，如果最值为 \(0\) 很显然这个区间的点都被删除了，不需要往下递归。注意到还有无效访问，如果这个点没被删除，但是他喝的两种冰红茶中(但实际上其实对于单点来说，同时只有一个不为 \(0\))的最大值都不满足至少为 \(k\) 的限制。

这里说说这种带删除操作的本质就是，暴力全部删去是简单的，复杂度不高的，瓶颈点在于快速判断而不能产生无效访问。基于上述，我们只能保证区间被删除的元素不会被重复无效访问，还要考虑没被删除的无需删除的元素不能无效访问。其实很容易的是，基于操作一维护的区间两种冰红茶最值都不满足 \(k\) 限制，那么这个区间就无需递归了。这样一来在操作一的基础上，我们在维护两个信息：

1. 区间存活的人数总和。

2. 区间最值，如果有存活的就是 \(1\) 否则为 \(0\)。

这样一来无论是否被删除，我们都能快速跳过无效信息，保证每次访问的点一定是可删的，这样的删点操作均摊下来至多 \(n\) 次。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}

template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 2e5 + 10;

struct Node
{
    int sum, mx; //存活的人数和,存活的最值(有人则为1,否则为0)
    ll add[2], val[2]; //两种区间加,两种区间最值
    bool cov[2]; //两种区间覆盖
} node[N << 2];

#define sum(x) node[x].sum
#define mx(x) node[x].mx
#define Add(x,y) node[x].add[y]
#define Cov(x,y) node[x].cov[y]
#define Val(x,y) node[x].val[y]

inline void TagCover(const int curr, const int idx)
{
    Add(curr, idx) = Val(curr, idx) = 0;
    Cov(curr, idx) = true;
}

inline void TagAdd(const int curr, const int idx, const ll val)
{
    Add(curr, idx) += val;
    Val(curr, idx) += val;
}

inline void push_up(const int curr)
{
    sum(curr) = sum(ls(curr)) + sum(rs(curr));
    mx(curr) = max(mx(ls(curr)),mx(rs(curr)));
    forn(i, 0, 1)
    {
        Val(curr, i) = max(Val(ls(curr), i),Val(rs(curr), i));
    }
}

inline void push_down(const int curr)
{
    forn(i, 0, 1)if (Cov(curr, i))TagCover(ls(curr), i), TagCover(rs(curr), i), Cov(curr, i) = false;
    forn(i, 0, 1)
    {
        if (Add(curr, i))
        {
            TagAdd(ls(curr), i,Add(curr, i)), TagAdd(rs(curr), i,Add(curr, i));
            Add(curr, i) = 0;
        }
    }
}

inline void merge(const int curr, const ll val)
{
    if (val > 0)
    {
        Add(curr, 0) += val;
        Val(curr, 0) += val;
        TagCover(curr, 1);
    }
    if (val < 0)
    {
        Add(curr, 1) -= val;
        Val(curr, 1) -= val;
        TagCover(curr, 0);
    }
}

int n, q;

inline void add(const int curr, const int l, const int r, const ll val, const int s = 1, const int e = n)
{
    if (l > r)return;
    const int mid = s + e >> 1;
    if (l <= s and e <= r)
    {
        merge(curr, val);
        return;
    }
    push_down(curr);
    if (l <= mid)add(ls(curr), l, r, val, s, mid);
    if (r > mid)add(rs(curr), l, r, val, mid + 1, e);
    push_up(curr);
}

inline void clear(const int curr)
{
    forn(i, 0, 1)
    {
        Add(curr, i) = Cov(curr, i) = Val(curr, i) = 0;
    }
    mx(curr) = sum(curr) = 0;
}

inline void del(const int curr, const int l, const int r, const ll val, const int s = 1, const int e = n)
{
    if (!mx(curr) or max(Val(curr, 0),Val(curr, 1)) < val)return;
    const int mid = s + e >> 1;
    if (s == e)
    {
        clear(curr);
        return;
    }
    push_down(curr);
    if (l <= mid)del(ls(curr), l, r, val, s, mid);
    if (r > mid)del(rs(curr), l, r, val, mid + 1, e);
    push_up(curr);
}

inline void build(const int curr = 1, const int l = 1, const int r = n)
{
    const int mid = l + r >> 1;
    if (l == r)
    {
        sum(curr) = mx(curr) = 1;
        return;
    }
    build(ls(curr), l, mid);
    build(rs(curr), mid + 1, r);
    push_up(curr);
}

inline void solve()
{
    cin >> n >> q;
    build();
    while (q--)
    {
        int op;
        cin >> op;
        if (op == 3)cout << sum(1) << endl;
        else
        {
            ll l, r, val;
            cin >> l >> r >> val;
            if (op == 1)add(1, l, r, val), add(1, 1, l - 1, -val), add(1, r + 1, n, -val);
            else del(1, l, r, val);
        }
    }
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

\[时间复杂度为：\ O(q\log{n})
\]