CF546E Soldier and Traveling 题解

CF546E Soldier and Traveling

英文原题：

当然Luogu有中文翻译

对于这种类型的题目，又是增加，又是减少的，我们可以使用网络流进行转化。

说句废话：

网络流这个东西，趣味十足，上可顶替匈牙利算法，下可转化动态规划。它似水一般灵活，总是可以出乎意料地解决问题。

而此题要使用到的是网络最大流之Dinic算法。

好了，说回来，看到这种题目，你有什么疑惑？

说说我的吧：

1. 信息这么多(\(a_i\) 和 \(b_i\))，怎么保存？

2. 这么多的点，无组织，无纪律，怎么办呢？

3. 这情况也太多了吧，怎么暴搜思考呢？

4. 即使知道可行，这题的输出怎么办呢？真恶心

我们从网络最大流的角度一个一个来思考吧！

1. 信息这么多，怎么保存？

我们可以把一个点的信息一分为2，让他们整齐罗列。

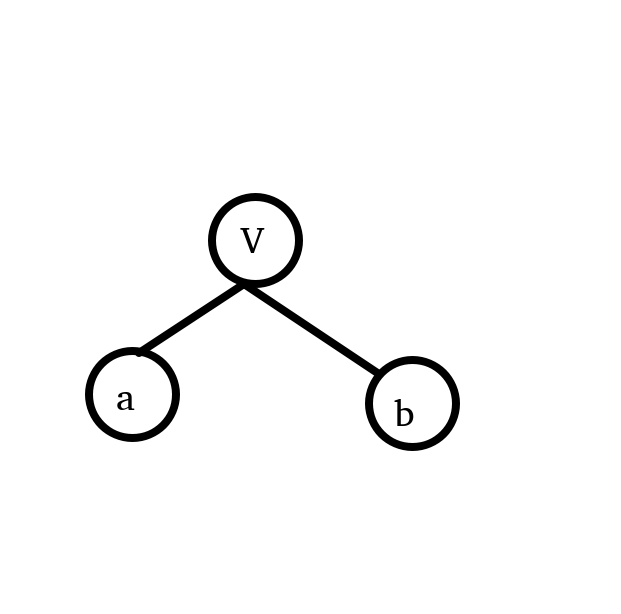
千万不要误以为 \(a_i\) 和 \(b_i\) 为节点，图中只是形象化地阐述“把一个点的信息一分为2”

2. 这么多的点，无组织，无纪律，怎么办呢？

那就找两个领导把他们汇总起来，这两个领导叫做源点以及汇点。

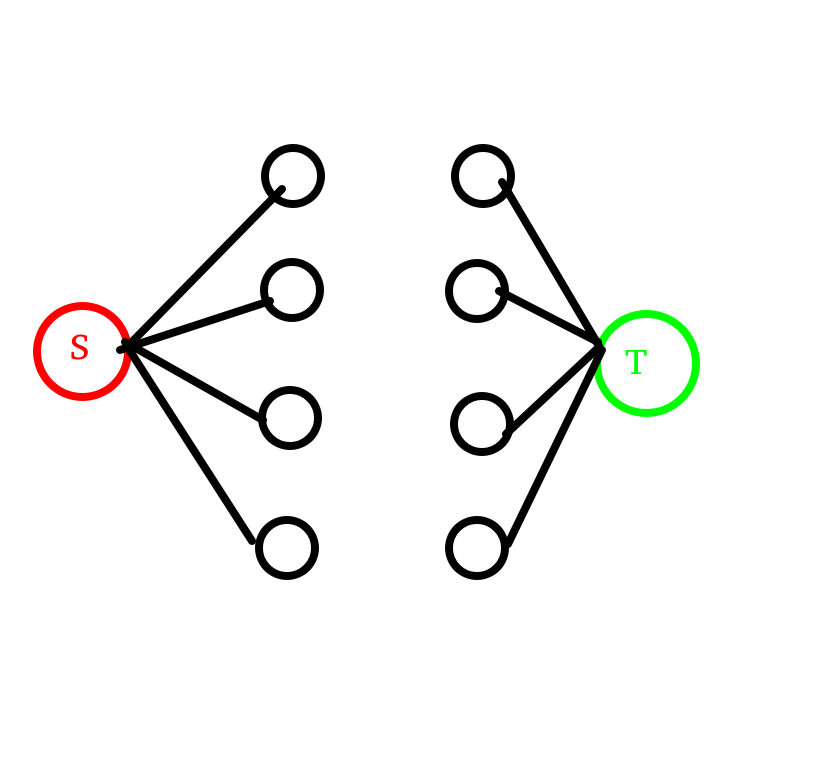
那流量是多少呢？

看图！

看左半部分，点 \(i\) 的流量为 \(a_i\)。

同理，右半部分流量为 \(b_i\)。

中间部分暂不考虑

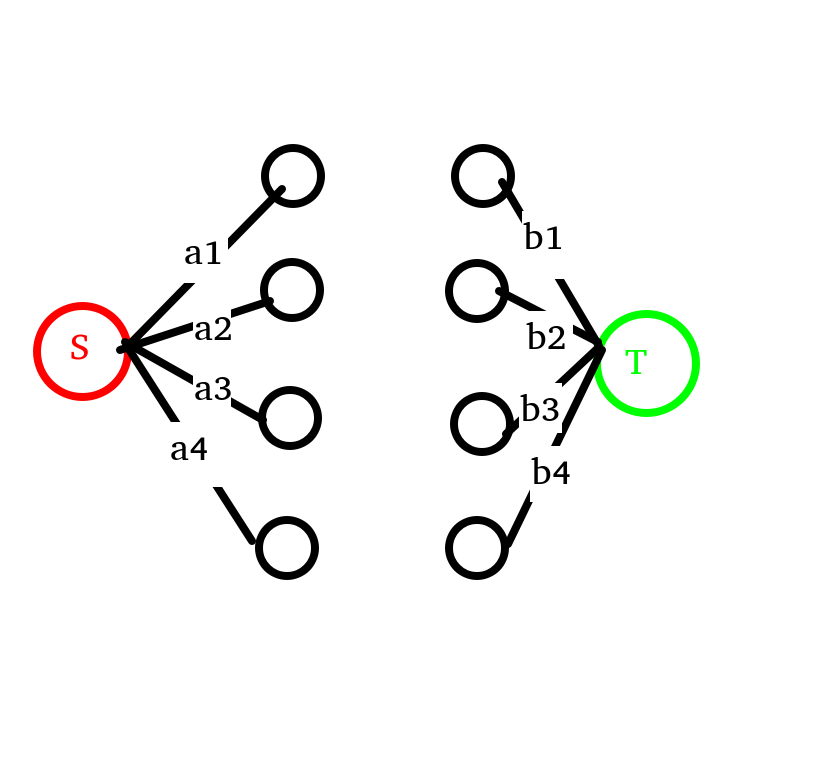
为什么要这样干呢？

现在假设 \(S\) 点有无穷无尽的水资源。

那么可以往每个左边的河道里塞满水，也就是对于左边的点 \(i\)（图中是靠近红点的四个点）的初始值为 \(a_i\)。

也就是对应题目中“每个点初始时有 \(a_i\) 个人”的条件。

同样的道理，经过中间一番乱七八糟的处理后，从右边流出的水应为 \(b_1,b_2,\dots,b_n\)，表示最终处理后，对于右边的点 \(i\) （图中是靠近绿点的四个点）最终为 \(b_i\)。

也就是对应题目中“每个点最终有 \(b_i\) 个人”的条件。

3. 这情况也太多了吧，怎么思考呢？

也就是考虑中间部分。

首先，有些人可以选择留下。那么对于这些点的水，随它们流，连接 \(n\) 条边，流量为 \(+∞\)。

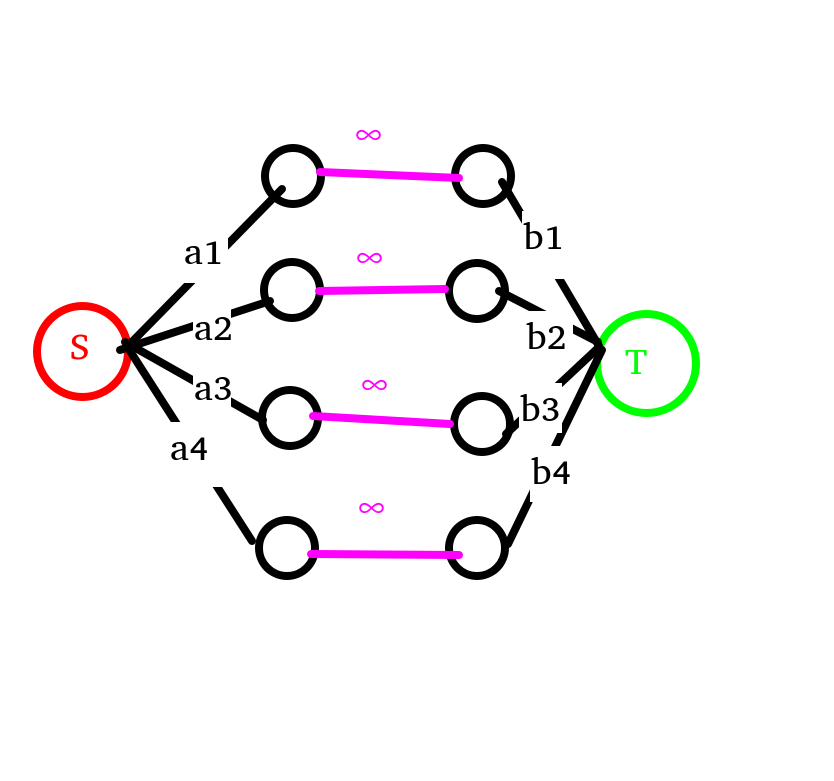
当然，如果有边相连，那也随便流，连接 \(m\) 条边（与题目中的 \(m\) 意义相同），如图（假设有这些边）。

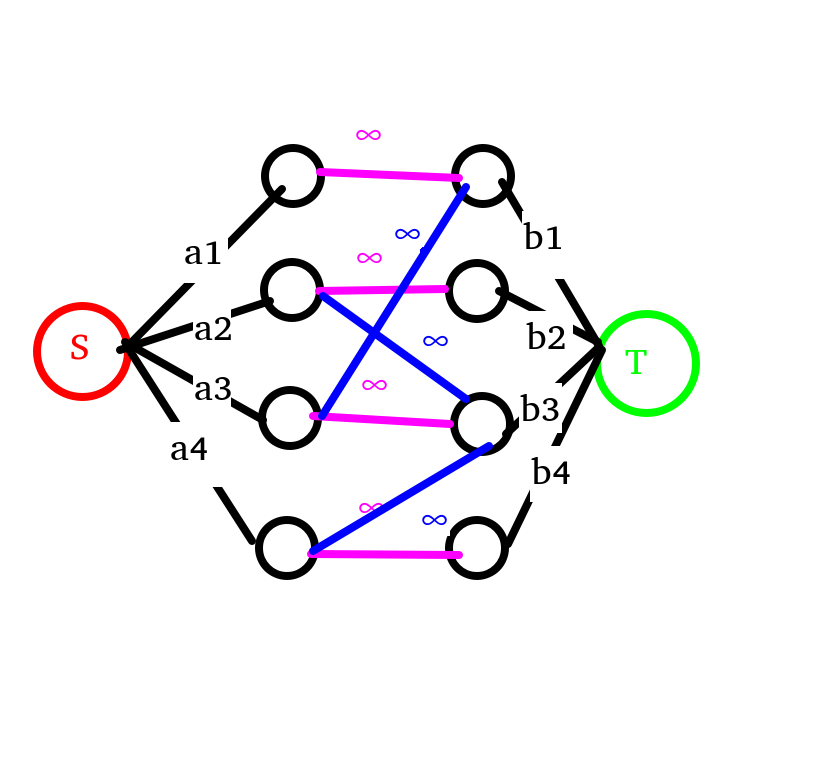
于是乎，跑一遍Dinic算法足矣！

1. 即使知道可行，这题的输出怎么办呢？真恶心

众所周知，Dinic会在找到增广路时，建立反边，以便反悔。

那么这些反边，就是我们利用的对象。

一条边的反边的权值不就是流过该边的流量吗？

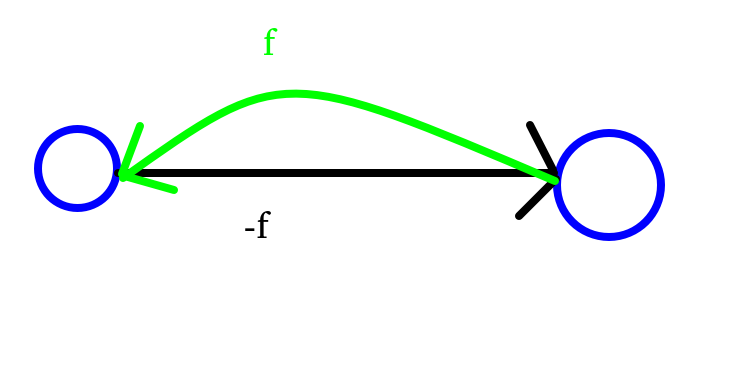
把中间部分的每条反边揪出来，在保存到一个数组里即可。

AC Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <numeric>

const int N = 210, M = 1410, INF = 1e9;

struct Node
{
	int to;
	int next;
	int w;
}e[M];

int head[N], cur[N], idx = 1;

void add(int a, int b, int c)           // 加边
{
	idx++;
	e[idx].to = b;
	e[idx].next = head[a];
	e[idx].w = c;
	head[a] = idx;

	idx++;
	e[idx].to = a;
	e[idx].next = head[b];
	e[idx].w = 0;
	head[b] = idx;
}

int n, m;
int a[N];
int b[N];
int S, T;
int sum1, sum2;				// sum1:a sum2:b

int d[N];

bool bfs()
{
	static int q[N];        // 队列
	int hh = 0, tt = 0;
	memset(d, 0, sizeof(d));
	q[0] = S;
	cur[S] = head[S];
	d[S] = 1;
	while (hh <= tt)
	{
		int t = q[hh++];
		for (int i = head[t]; i; i = e[i].next)
		{
			int to = e[i].to;
			if (!d[to] && e[i].w)
			{
				cur[to] = head[to];
				d[to] = d[t] + 1;
				q[++tt] = to;
				if (to == T) return true;
			}
		}
	}
	return false;
}

int dinic(int u, int limit)
{
	if (u == T) return limit;
	int rest = limit;
	for (int i = cur[u]; i && rest; i = e[i].next)
	{
		cur[u] = i;
		int to = e[i].to;
		if (d[to] == d[u] + 1 && e[i].w)
		{
			int k = dinic(to, std::min(rest, e[i].w));
			if (!k) d[to] = 0;
			rest -= k;
			e[i].w -= k;
			e[i ^ 1].w += k;
		}
	}
	return limit - rest;
}

int map[N][N];                  // 记录反边信息，即结果

int main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	std::cin >> n >> m;
	for (int i = 1; i <= n; i++)std::cin >> a[i];
	for (int i = 1; i <= n; i++)std::cin >> b[i];
	sum1 = std::accumulate(a + 1, a + n + 1, 0);    // 求和
	sum2 = std::accumulate(b + 1, b + n + 1, 0);
	if(sum1 != sum2)        //直接排除
	{
		std::cout << "NO" << '\n';
		return 0;
	}
	for (int i = 1; i <= n; i++) add(0, i, a[i]);   // 左
	for (int i = n + 1; i <= n * 2; i++) add(i, n * 2 + 1, b[i - n]);   // 右
	for (int i = 1; i <= n; i++) add(i, i + n, INF);                // 中1
	for (int i = 1; i <= m; i++)        // 中2
	{
		int a, b;
		std::cin >> a >> b;
		add(a, b + n, INF);
		add(b, a + n, INF);
	}
	S = 0, T = n * 2 + 1;

	auto query = [&]()					// Dinic 模板
	{
		int maxflow = 0, flow = 0;
		while (bfs())
		{
			while (flow = dinic(S, INF))
			{
				maxflow += flow;
			}
		}
		return maxflow;
	};

	if (query() != sum1)                // 直接排除
	{
		std::cout << "NO" << '\n';
		return 0;
	}
	else                                // 扣反边
	{
		std::cout << "YES" << '\n';
		int t = 4 * n + 2;
		for (int i = 1; i <= 2 * m + n; i++)
		{
			map[e[t ^ 1].to][e[t].to - n] += e[t ^ 1].w;                        // 注意要 -n
			t += 2;
		}
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				std::cout << map[i][j] << ' ';
			}
			std::cout << '\n';
		}
	}
	return 0;
}