力扣1235(java)-规划兼职工作（困难）

题目：

你打算利用空闲时间来做兼职工作赚些零花钱。

这里有 n 份兼职工作，每份工作预计从 startTime[i] 开始到 endTime[i] 结束，报酬为 profit[i]。

给你一份兼职工作表，包含开始时间 startTime，结束时间 endTime 和预计报酬 profit 三个数组，请你计算并返回可以获得的最大报酬。

注意，时间上出现重叠的 2 份工作不能同时进行。

如果你选择的工作在时间 X 结束，那么你可以立刻进行在时间 X 开始的下一份工作。

示例 1：

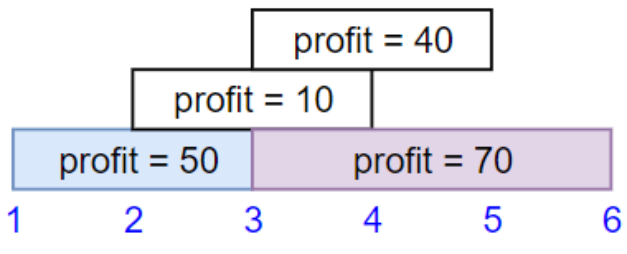
输入：startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出：120
解释：
我们选出第 1 份和第 4 份工作，
时间范围是 [1-3]+[3-6]，共获得报酬 120 = 50 + 70。

示例2：

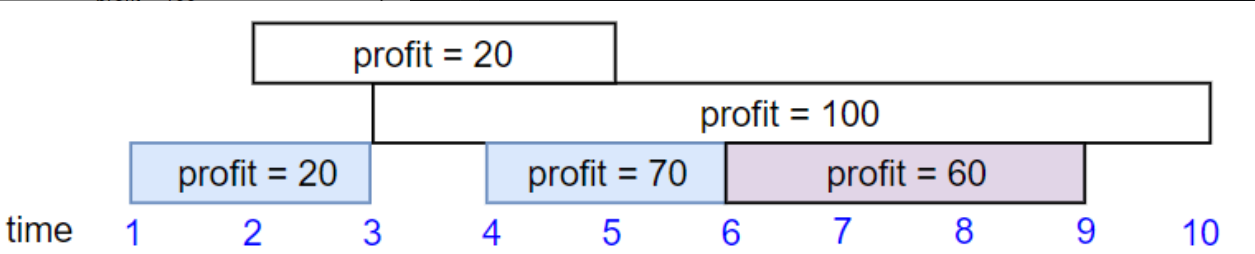
输入：startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出：150
解释：
我们选择第 1，4，5 份工作。
共获得报酬 150 = 20 + 70 + 60。

示例 3：

输入：startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出：6

提示：

1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
1 <= startTime[i] < endTime[i] <= 10^9
1 <= profit[i] <= 10^4

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-profit-in-job-scheduling
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

动态规划+二分查找：

1.首先将兼职工作按结束时间从小到大进行排序；

2.dp[i]：表示第 i 份工作可以获得的最大报酬，初始化dp[0] = 0；

3.则最大报酬可以分情况讨论：

• 如果不选择第 i 份工作：则dp[i] = dp[i-1]；
• 如果选择第 i 份工作：那么此时的结果就是当前工作的收获+小于当前工作开始时间的最大结束时间，此时又可以使用二分查找来解决小于某一个数最大的位置。所以：dp[i] = dp[j] + profit[i];
• 两者取最大值：dp[i] = max(dp[i-1]，dp[j] + profit[i])

java代码：

 1 class Solution {
 2     public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
 3         int n = startTime.length;
 4         int[] dp = new int[n+1];
 5         int[][] jobs = new int[n][3];
 6         for(int i = 0; i < n; i++){
 7             jobs[i] = new int[]{startTime[i], endTime[i], profit[i]};
 8         }
 9         //按照结束时间从小到大排序
10         Arrays.sort(jobs, (a,b)->a[1]-b[1]);
11         for(int i = 0; i < n; i++){
12             int max = binarySearch(jobs, i, jobs[i][0]);
13             dp[i+1] = Math.max(dp[i], dp[max] + jobs[i][2]);
14         }
15         return dp[n];
16
17     }
18     //使用二分查找，找到小于下一个开始时间的最大结束时间
19     //right：当前位置， target:当前位置的开始时间
20     public int binarySearch(int[][] jobs, int right, int target){
21         int left = 0;
22         while(left < right){
23             int mid = (left + right) / 2;
24             if(jobs[mid][1] <= target){
25                 left = mid + 1;
26             }else{
27                 right = mid;
28             }
29         }
30         return left;
31     }
32 }