【二分答案】P2390 地标访问

\(\color{black}\text{P2390 地标访问 (传送门)}\)

学过区间 DP 的，看到这题的第一反应都是：访问的地标一定是一个区间，并且在不断扩大，区间 DP！可看到数据范围，又瞬间放弃了。与 P1220 关路灯 不同，这题由于没有电量的消耗等额外因素，有这样一个小性质：

• 贝西的行走路线只可能是三种：一路向左，一路向右或者在中途折返一次。

一路向左和一路向右倒还好理解，可为什么最多只会折返一次呢？考虑以下情况：

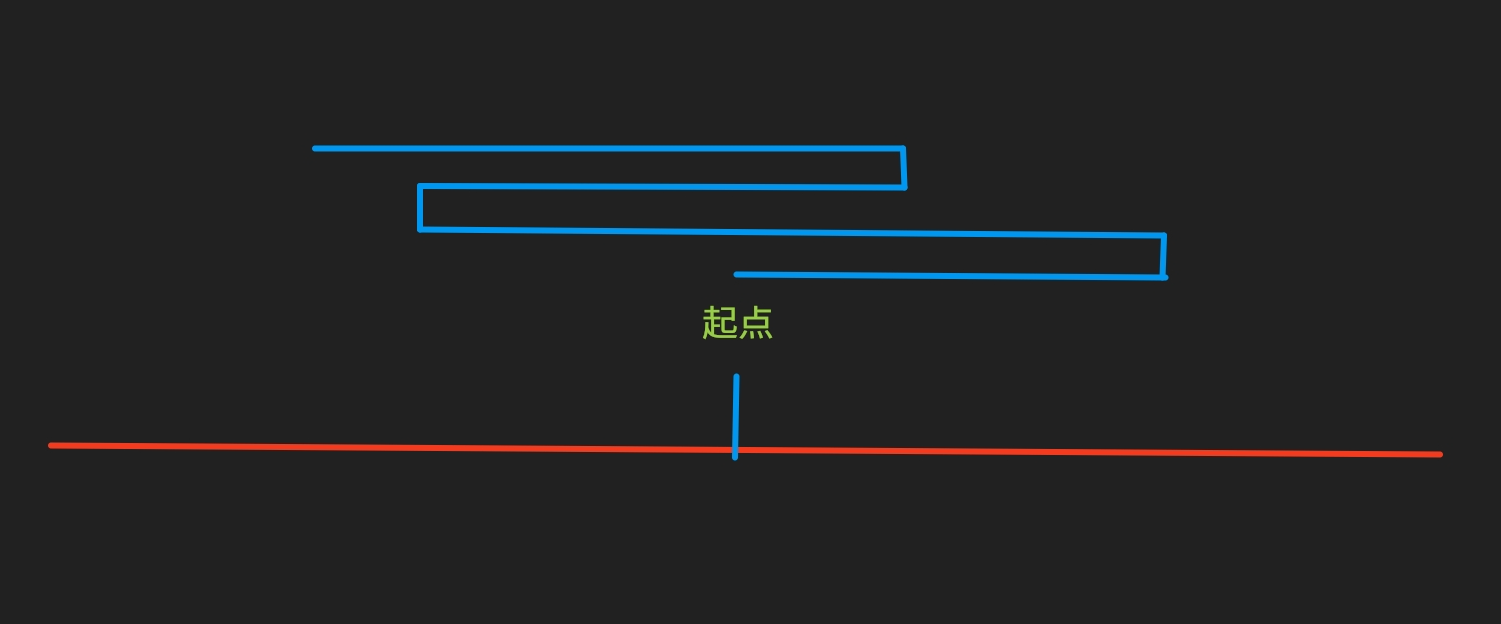
如图，贝西从起点出发，折返了多次以访问所有地标。可问题是，以下做法不仅能满足要求，也更优：

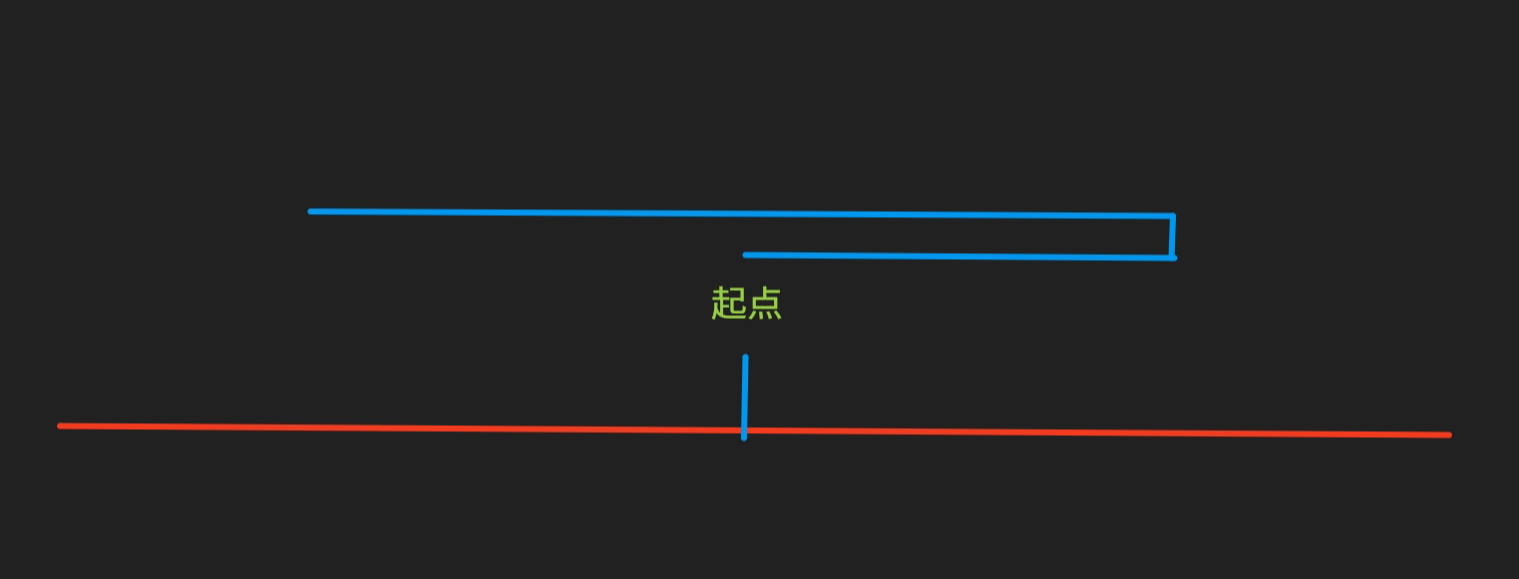
换句话说，由于我们访问的地标总是一个区间，而从某个点开始走完整个区间分为三种情况：

1. 起点在区间左边，一路向右；
2. 起点在区间右边，一路向左；
3. 起点在区间里，先前往比较近的端点（左端点或者右端点），再前往另一个端点走完整个区间。

那么，现在问题来了：我们到底能走多少个地标呢？这取决于我们拥有的时间 \(t\)。换句话说，这是在满足条件（所用时间 \(\bm{\le t}\)）的情况下找最值。这不就是一个二分答案吗？而且单调性也是显然的：如果不能访问 \(x\) 个地标，那也访问不了 \(y(y>x)\) 个地标；如果能访问 \(x\) 个地标，那也访问的了 \(y(y<x)\) 个地标。

考虑二分答案。难点在于，如何设计 \(\text{check}\) 函数？假设当前二分答案猜测可以访问 \(X\) 个地标，则需要选择连续的 \(X\) 个地标（地标已经按坐标大小排序），即 \(x_1,x_2,\dots,x_X\) 或者 \(x_2,x_3,\dots,x_{X+1}\) 或者 \(x_3,x_4,\dots,x_{X+2}\ \dots\) 我们可以枚举这些区间的终点 \(i\in[X,n]\)，则区间的起点为 \(st=i-X+1\)。考虑上面的三种情况：一路向右，一路向左，起点在区间里，只要有一个满足条件就返回 \(\text{True}\)。条件判断的表达式分别为：

x[st] >= 0 && x[i] <= t

x[i] <= 0 && abs(x[st]) <= t

x[st] <= 0 && x[i] >= 0 && min(abs(x[st]), x[i]) + x[i] - x[st] <= t

完全再现了上面的三种情况。

如此一来，代码也就非常好写了：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int N = 5e4 + 5;

int t, n, a[N];

bool check(int X) {
	for (int i = X; i <= n; i++) {
		int st = i - X + 1;
		if (a[st] >= 0 && a[i] <= t)
			return 1;
		else if (a[i] <= 0 && abs(a[st]) <= t)
			return 1;
		else if (a[st] <= 0 && a[i] >= 0 && min(abs(a[st]), a[i]) + a[i] - a[st] <= t)
			return 1;
	}
	return 0;
}

signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> t >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	sort(a + 1, a + 1 + n);
	int l = -1, r = 5e4 + 1;
	while (l + 1 < r) {
		int mid = l + r >> 1;
		if (check(mid))
			l = mid;
		else
			r = mid;
	}
	cout << l;
	return 0;
}