POJ 1655 - Balancing Act - [DFS][树的重心]

链接：http://poj.org/problem?id=1655

Time Limit: 1000MS Memory Limit: 65536K

Description

Consider a tree T with N (1 <= N <= 20,000) nodes numbered 1...N. Deleting any node from the tree yields a forest: a collection of one or more trees. Define the balance of a node to be the size of the largest tree in the forest T created by deleting that node from T.
For example, consider the tree:

Deleting node 4 yields two trees whose member nodes are {5} and {1,2,3,6,7}. The larger of these two trees has five nodes, thus the balance of node 4 is five. Deleting node 1 yields a forest of three trees of equal size: {2,6}, {3,7}, and {4,5}. Each of these trees has two nodes, so the balance of node 1 is two.

For each input tree, calculate the node that has the minimum balance. If multiple nodes have equal balance, output the one with the lowest number.

Input

The first line of input contains a single integer t (1 <= t <= 20), the number of test cases. The first line of each test case contains an integer N (1 <= N <= 20,000), the number of congruence. The next N-1 lines each contains two space-separated node numbers that are the endpoints of an edge in the tree. No edge will be listed twice, and all edges will be listed.

Output

For each test case, print a line containing two integers, the number of the node with minimum balance and the balance of that node.

Sample Input

1
7
2 6
1 2
1 4
4 5
3 7
3 1

Sample Output

1 2

题意：

给出一棵 $N$ 个节点（编号为 $1 \sim N$）的树。

对于树上某一个节点 $x$，如果我们把它从树中删除，那么原来的一棵树就可能会变成若干棵树，或者说，一个森林；

设 ${\rm{maxpart}}(x)$ 为该森林中节点最多的那一棵树的大小。那么，使得 ${\rm{maxpart}}(x)$ 取得最小值的节点就称为树的重心。

本题要求给出树的重心的编号（如果有多个重心，则给出其中编号最小的），以及其对应的 ${\rm{maxpart}}(x)$。

题解：

实际上，一次DFS就可以求得重心和对应的 ${\rm{maxpart}}(x)$。

如图，节点 $4$ 就是这棵树的重心，且 ${\rm{maxpart}}(4) = \max(n-size[4],size[4],size[6])$。

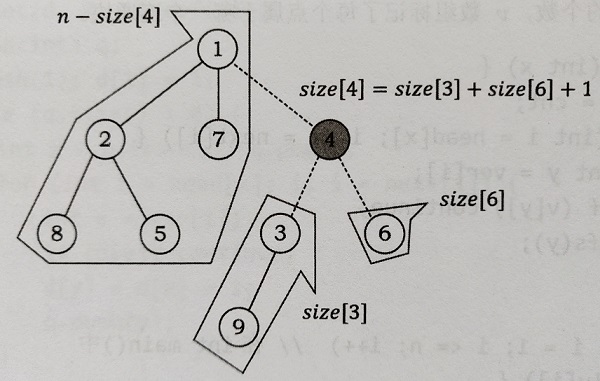（图片转载自李煜东《算法竞赛进阶指南》）

AC代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=2e4+;

int n;

struct Edge{
    int u,v;
    Edge(int _u=,int _v=){u=_u,v=_v;}
};
vector<Edge> E;
vector<int> G[maxn];
void init(int l,int r)
{
    E.clear();
    for(int i=l;i<=r;i++) G[i].clear();
}
void addedge(int u,int v)
{
    E.push_back(Edge(u,v));
    G[u].push_back(E.size()-);
}

int siz[maxn],vis[maxn];
pair<int,int> center;
void dfs(int now)
{
    vis[now]=; siz[now]=;
    int maxpart=;
    for(int i=;i<G[now].size();i++)
    {
        Edge &e=E[G[now][i]]; int nxt=e.v;
        if(vis[nxt]) continue;
        dfs(nxt);
        siz[now]+=siz[nxt];
        maxpart=max(maxpart,siz[nxt]);
    }
    maxpart=max(maxpart,n-siz[now]);
    if(maxpart<center.first || (maxpart==center.first && now<center.second))
    {
        center.first=maxpart;
        center.second=now;
    }
}

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%d",&n);
        init(,n);
        for(int i=,u,v;i<n;i++)
        {
            scanf("%d%d",&u,&v);
            addedge(u,v);
            addedge(v,u);
        }

        center=make_pair(INF,);
        memset(vis,,sizeof(vis));
        dfs();
        printf("%d %d\n",center.second,center.first);
    }
}