全排列-hdu1027

题目描述：

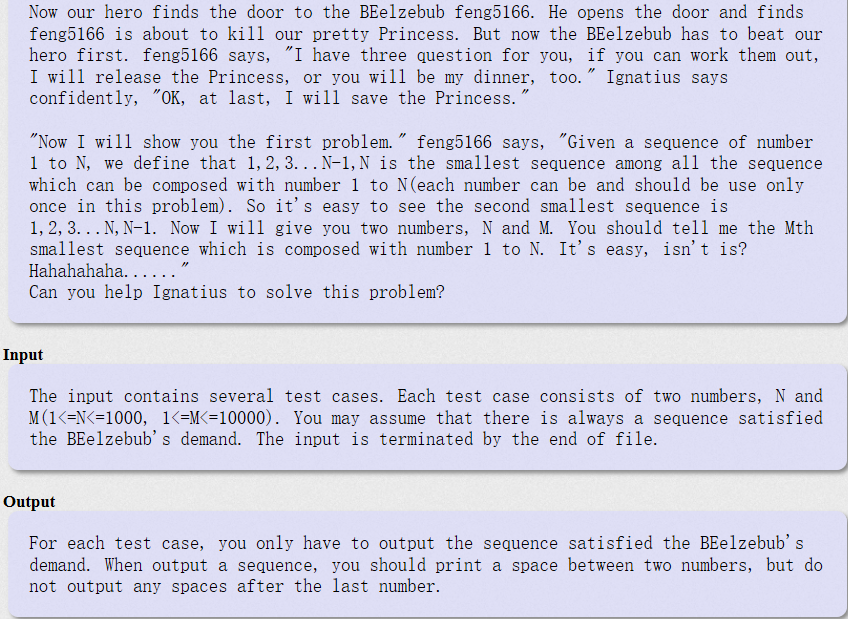
题目大意：现在给我们两个数字，N和M。我们应该编程找出由1到N组成的第M个最小序列。主要运用了全排列的思想，运用了全排列中next_permutation（）函数；

next_permutation 使用方法：next_permutation(数组头地址，数组尾地址);若下一个排列存在，则返回真，如果不存在则返回假

举例：

对于数组a={1,2,3};

do
{
　　cout<<a[0]<<" "<<a[1]<<" "<<a[2]<<endl;
} while (next_permutation(a,a+3));//参数3指的是要进行排列的长度

输出的是：

1 2 3
 1 3 2
 2 1 3
 2 3 1
 3 1 2
 3 2 1

如果改成 while(next_permutation(a,a+2))，则输出：
 1 2 3
 2 1 3
只对前两个元素进行字典排序，显然，如果改成 while(next_permutation(a,a+1)); 则只输出：1 2 3
 代码实现：

#include<stdio.h>
#include<algorithm>
#include<cmath>
using namespace std;
int main()
{
    int a[];
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=;i<n;i++)
            a[i]=i+;
        for(int i=;i<m;i++)
        {
            next_permutation(a,a+n);//每执行一次，就重新排序一次
            if(i==m-)//执行m-1次后输出结果
            {
                for(int j=;j<n-;j++)
                    printf("%d ",a[j]);
                printf("%d\n",a[n-]);
            }
        }
    }
    return ;
}