归一化(softmax)、信息熵、交叉熵

机器学习中经常遇到这几个概念，用大白话解释一下：

一、归一化

把几个数量级不同的数据，放在一起比较（或者画在一个数轴上），比如：一条河的长度几千甚至上万km，与一个人的高度1.7m，放在一起，人的高度几乎可以被忽略，所以为了方便比较，缩小他们的差距，但又能看出二者的大小关系，可以找一个方法进行转换。

另外，在多分类预测时，比如：一张图，要预测它是猫，或是狗，或是人，或是其它什么，每个分类都有一个预测的概率，比如是猫的概率是0.7，狗的概率是0.1，人的概率是0.2... , 概率通常是0到1之间的数字，如果我们算出的结果，不在这个范围，比如：700，10，2 ，甚至负数，这样就需要找个方法，将其转换成0-1之间的概率小数，而且通常为了满足统计分布，这些概率的和，应该是1。

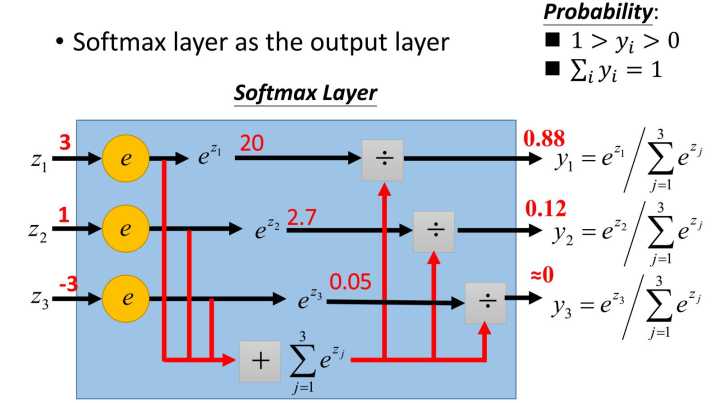
最常用的处理方法，就是softmax，原理如上图（网上淘来的）。

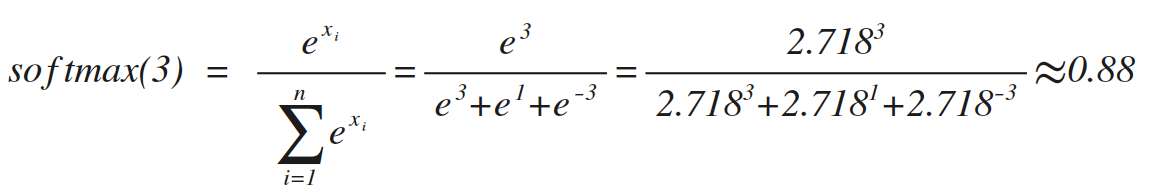
类似的softmax(1)=0.12，softmax(-3)=0，这个方法在数学上没毛病，但是在实际运用中，如果目标值x很大，比如10000，那e的10000次方，很可能超出编程语言的表示范围，所以通常做softmax前，要对数据做一下预处理（比如：对于分类预测，最简单的办法，所有训练集整体按比例缩小）

二、信息熵

热力学中的热熵是表示分子状态混乱程度的物理量，而且还有一个所谓『熵增原理』，即：宇宙中的熵总是增加的，换句话说，分子状态总是从有序变成无序，热量总是从高温部分向低温部分传递。 香农借用了这个概念，用信息熵来描述信源的不确定度。

简单点说，一个信息源越不确定，里面蕴含的信息量越大。举个例子：吴京《战狼2》大获成功后，说要续拍《战狼3》，但是没说谁当女主角，于是就有各种猜测，各种可能性，即：信息量很大。但是没过多久，吴京宣布女主角确定后，大家就不用再猜测女主角了，信息量相比就没这么大了。

这个例子中，每种猜测的可能性其实就是概率，而信息量如何衡量，可以用下面的公式来量化计算，算出来的值即信息熵：

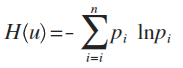
这里p为概率，最后算出来的结果通常以bit为单位。

举例：拿计算机领域最常现的编码问题来说，如果有A、B、C、D这四个字符组成的内容，每个字符出现的概率都是1/4，即概率分布为{1/4，1/4，1/4，1/4}，设计一个最短的编码方案来表示一组数据，套用刚才的公式：

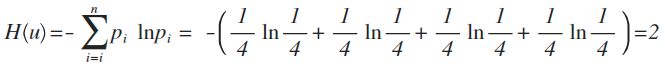
即：2个bit，其实不用算也能想明白，如果第1位0表示A，1表示B；第2位0表示C，1表示D，2位编码搞定。

如果概率变了，比如A、B、C、D出现的概率是{1，1，1/2，1/2}，即：每次A、B必然出现，C、D出现机会各占一半，这样只要1位就可以了。1表示C，0表示D，因为AB必然出现，不用表示都知道肯定要附加上AB，套用公式算出来的结果也是如此。

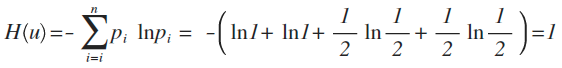
三、交叉熵

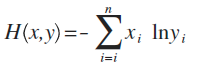
这是公式定义，x、y都是表示概率分布（注：也有很多文章喜欢用p、q来表示），这个东西能干嘛呢？

假设x是正确的概率分布，而y是我们预测出来的概率分布，这个公式算出来的结果，表示y与正确答案x之间的错误程度（即：y错得有多离谱），结果值越小，表示y越准确，与x越接近。

比如：

x的概率分布为：{1/4 ，1/4，1/4，1/4}，现在我们通过机器学习，预测出来二组值：

y1的概率分布为  {1/4 ,  1/2 , 1/8 , 1/8}

y2的概率分布为  {1/4 ,  1/4 , 1/8 , 3/8}

从直觉上看，y2分布中，前2项都100%预测对了，而y1只有第1项100%对，所以y2感觉更准确，看看公式算下来，是不是符合直觉：

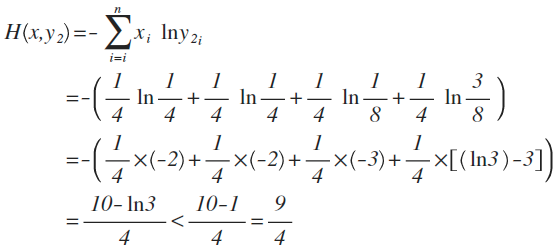
对比结果，H(x,y1)算出来的值为9/4，而H(x,y2)的值略小于9/4，根据刚才的解释，交叉熵越小，表示这二个分布越接近，所以机器学习中，经常拿交叉熵来做为损失函数(loss function)。

参考文章：

https://www.zhihu.com/question/23765351
https://www.zhihu.com/question/41252833/answer/108777563
https://www.zhihu.com/question/22178202