图->存储结构->邻接表

文字描述

　　邻接表是图的一种链式存储结构。在邻接表中，对图中每个顶点建立一个单链表，第i个单链表的结点表示依附顶点vi的边(对有向图是指以顶点vi为尾的弧)。单链表中的每个结点由3个域组成，其中邻接点域adjvex指示与顶点vi邻接的点在图中的位置；链域nextarc指示下一条边或弧的结点；数据域info存储和边或弧相关的信息如权值等。每个链表上附设一个表头结点，在表头结点中，除了设有链域firstarc指向链表中第一个结点外，还设有存储顶点vi的名或其他有关信息的数据域data。

　　在无向图的邻接表中，顶点vi的度恰为第i个单链表中的结点数；而在有向图中，第i个链表中的结点数只是顶点vi的出度，为求入度，需便历整个邻接表；为了方便确定顶点的入度或以顶点vi为头的弧，可以建立一个有向图的逆邻接表，即对每个顶点vi建立一个了链接以vi为头的弧的表。

示意图

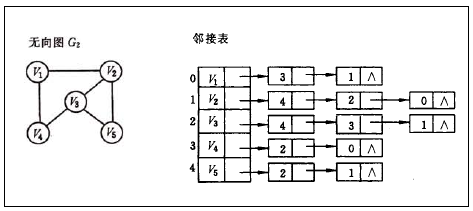
算法分析

　　在建立邻接表或逆邻接表时，若输入的顶点信息就是顶点的编号，则建立邻接表的时间复杂度为n+e；否则，需要通过查找才能得到顶点在图中位置，则时间复杂度为n*e.

　　在邻接表上容易找到任一顶点的第一个邻接点和下一个领接点，但要判定任意两个顶点(vi和vj)之间是否有边或弧相连，则需搜索第i个或第j个链表；因此，不及邻接矩阵方便。

代码实现

 /*
     以邻接表作为图的存储结构创建图。
 */

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>

 #define INFINITY        100000    //最大值
 #define    MAX_VERTEX_NUM    20        //最大顶点数
 #define None        -1
 typedef enum {DG, DN, UDG, UDN} GraphKind; //{有向图，有向网，无向图，无向网}
 typedef char VertexType;
 typedef struct{
     char note[];
 }InfoType;
 //表结点
 typedef struct ArcNode{
     int adjvex;    //该弧所指向的顶点的位置
     struct ArcNode *nextarc;    //指向下一条弧的指针
     InfoType *info;    //该弧相关信息的指针
 }ArcNode;
 //头结点
 typedef struct VNode{
     VertexType data;//顶点信息
     ArcNode *firstarc;//指向第一条依附该顶点的弧的指针
 }VNode, AdjList[MAX_VERTEX_NUM];
 typedef struct{
     AdjList vertices;
     int vexnum;//图的顶点数
     int arcnum;//图的弧数
     int kind; //图的种类标志
 }ALGraph;

 /*
     若G中存在顶点u，则返回该顶点在图中位置；否则返回-1。
 */
 int LocateVex(ALGraph G, VertexType v)
 {
     int i = ;
     for(i=; i<G.vexnum; i++){
         if(G.vertices[i].data == v){
             return i;
         }
     }
     return -;
 }

 /*
     在链表L的头部前插入v
 */
 int InsFirst(ArcNode *L, int v)
 {
     ArcNode *n = (ArcNode *)malloc(sizeof(struct ArcNode));
     n->adjvex = v;
     n->nextarc = L->nextarc;
     L->nextarc = n;
     return ;
 }

 /*
     采用邻接表的存储结构，构造无向图
  */
 int CreateUDG(ALGraph *G)
 {
     int i = , j = , k = , IncInfo = ;
     int v1 = , v2 = ;
     char tmp[] = {};

     printf("输入顶点数，弧数，其他信息标志位: ");
     scanf("%d,%d,%d", &G->vexnum, &G->arcnum, &IncInfo);

     for(i=; i<G->vexnum; i++){
         printf("输入第%d个顶点: ", i+);
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         G->vertices[i].data = tmp[];
         G->vertices[i].firstarc = malloc(sizeof(struct ArcNode));
         G->vertices[i].firstarc->adjvex = None;
         G->vertices[i].firstarc->nextarc = NULL;
     }

     for(k=; k<G->arcnum; k++){
         printf("输入第%d条弧(顶点1, 顶点2): ", k+);
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         sscanf(tmp, "%c,%c", &v1, &v2);
         i = LocateVex(*G, v1);
         j = LocateVex(*G, v2);
         InsFirst(G->vertices[i].firstarc, j);
         InsFirst(G->vertices[j].firstarc, i);
         if(IncInfo){
             //other info on arc
         }
     }
     return ;
 }

 /*
     采用邻接表的存储结构，构造图
 */
 int CreateGraph(ALGraph *G)
 {
     printf("输入图类型: -有向图(0), -有向网(1), +无向图(2), -无向网(3): ");
     scanf("%d", &G->kind);
     switch(G->kind){
         case DG:
         case DN:
         case UDN:
             printf("还不支持!\n");
             return -;
         case UDG:
             return CreateUDG(G);
         default:
             return -;
     }
 }

 /*
     输出图的信息
 */
 void printG(ALGraph G)
 {
     if(G.kind == DG){
         printf("类型：有向图；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }else if(G.kind == DN){
         printf("类型：有向网；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }else if(G.kind == UDG){
         printf("类型：无向图；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }else if(G.kind == UDN){
         printf("类型：无向网；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }
     int i = ;
     ArcNode *p = NULL;
     for(i=; i<G.vexnum; i++){
         printf("%c\t", G.vertices[i].data);
         p = G.vertices[i].firstarc;
         while(p){
             if(p->adjvex != None)
                 printf("%d\t", p->adjvex);
             p = p->nextarc;
         }
         printf("\n");
     }
     return;
 }

 int main(int argc, char *argv[])
 {
     ALGraph G;
     if(CreateGraph(&G) > -){
         printG(G);
     }
     return ;
 }

邻接表存储结构(图)

代码运行