python中修改工作目录
python中修改工作目录的更多相关文章
- python获得当前工作目录和修改
import os curDir = os.getcwd() 最近使用Python 写了很多脚本,想导入脚本,发现不知道如何查看python 的默认工作目录,并修改默认工作目录. 方法/步骤 查 ...
- Jupyter修改工作目录(Anaconda环境)
Anaconda安装时未添加环境变量 1.打开Anaconda Prompt 输入jupyter notebook --generate-config (base) C:\Users\Sroxi> ...
- jenkins 修改工作目录
修改Jenkins路径 Jenkins的默认安装路径是/var/lib/jenkins 现在由于这个根目录的磁盘太小,所以切换到/data 目录下. Jenkins目录.端口.工作目录等信息在/etc ...
- Python快速定位工作目录
原文链接:http://www.cnblogs.com/wdong/archive/2010/08/19/1802951.html 常年奋斗在编码一线的同学,应该都深有体会,工作久了,很多项目文件.技 ...
- .NET中的工作目录一览!
定义: 当前工作目录——进行某项操作的目的目录,会随着OpenFileDialog.SaveFileDialog等对象所确定的目录而改变. 当前执行目录——该进程从中启动的目录,即文件自身 ...
- python中修改字符串的几种方法
在Python中,字符串是不可变类型,即无法直接修改字符串的某一位字符.因此改变一个字符串的元素需要新建一个新的字符串.常见的修改方法有以下4种. 方法1:将字符串转换成列表后修改值,然后用join组 ...
- 在TFS 2013的迭代视图中修改工作项数目限制
当TFS迭代中的工作项数目超过500时,在TFS的网页(Web Access)显示中就会出现红色警告提示"积压工作(backlog)中的项数超出配置的限制500.当前总数为529-.&quo ...
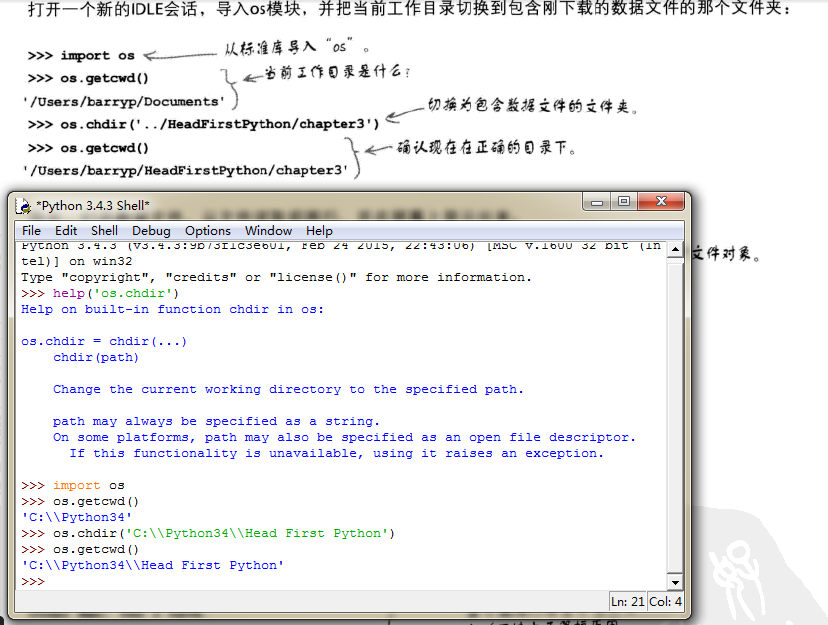
- Python 改变当前工作目录
在shell里编辑: import os os.getcwd() #取得当前工作目录 os.chdir(r'目标目录') # os.chdir(r'd:\learnpy')
- eclipse修改工作目录颜色
转载请注明本地址,http://blog.csdn.net/u013173247/article/details/41676495 经常用Eclipse的朋友都应该清楚,Eclipse的白背景不知道晃 ...
随机推荐
- HAProxy+keepalived+MySQL 实现MHA中slave集群负载均衡的高可用
HAProxy+keepalived+MySQL实现MHA中slave集群的负载均衡的高可用 Ip地址划分: 240 mysql_b2 242 mysql_b1 247 haprox ...
- python之attrgetter函数对对象排序
# 使用attrgetter函数对对象排序 # attrgetter处理对象,itemgetter处理序列 from operator import attrgetter class user(): ...
- 【gridview增删改查】数据库查询后lodop打印
ASP.NET中使用gridview可以很容易的把需要的数据动态显示在前台,还可以在表格里加入列进行增删改查,每次点击的时候重新加载数据,gridview也提供了分页等功能,还有一些模版让显示在前台的 ...
- QueryParser 是对一段话进行分词的 用于收集客户端发来的
- Get The Treasury HDU - 3642(扫描线求三维面积交。。体积交)
题意: ...就是求体积交... 解析: 把每一层z抽出来,计算面积交, 然后加起来即可..! 去看一下 二维面积交的代码 再看看这个三维面积交的代码.. down函数里 你发现了什么规律!!! 参考 ...
- 【刷题】AtCoder Regular Contest 001
A.センター採点 题意:给一个只包含1.2.3.4的字符串,求出现次数最多和最少的字符 做法:还能怎么做... #include<bits/stdc++.h> #define ui uns ...
- Java创建文件
public class FileTest { public static void main(String[] args) throws IOException { File file = new ...
- 在Sqlite中通过Replace来实现插入和更新
你可能在批量处理一个事务的时候,想要批量插入一系列的数据,但是这些数据当添加完一次之后,重新添加的时候,你不想要重新添加,只是想将原有的数据进行更新,例如:我想要通过Excel将一系列的图书导入到 ...
- 图片缓存:浏览器刷新 和 304 Not Modified 与 If-Modified-Since 及 Cache-Control
关键词:浏览器刷新,304 Not Modified ,If-Modified-Since,Cache-Control,Expires 今天在用chrome浏览淘宝页面的时候,发现很多来自淘宝图片HT ...
- 装饰页面decorators.xml
WEB-INF/decorators.xml 这个配置可以增加页面的 装饰页面
